Binxu Wang
Circuit Mechanisms for Spatial Relation Generation in Diffusion Transformers
Jan 09, 2026Abstract:Diffusion Transformers (DiTs) have greatly advanced text-to-image generation, but models still struggle to generate the correct spatial relations between objects as specified in the text prompt. In this study, we adopt a mechanistic interpretability approach to investigate how a DiT can generate correct spatial relations between objects. We train, from scratch, DiTs of different sizes with different text encoders to learn to generate images containing two objects whose attributes and spatial relations are specified in the text prompt. We find that, although all the models can learn this task to near-perfect accuracy, the underlying mechanisms differ drastically depending on the choice of text encoder. When using random text embeddings, we find that the spatial-relation information is passed to image tokens through a two-stage circuit, involving two cross-attention heads that separately read the spatial relation and single-object attributes in the text prompt. When using a pretrained text encoder (T5), we find that the DiT uses a different circuit that leverages information fusion in the text tokens, reading spatial-relation and single-object information together from a single text token. We further show that, although the in-domain performance is similar for the two settings, their robustness to out-of-domain perturbations differs, potentially suggesting the difficulty of generating correct relations in real-world scenarios.
An Analytical Theory of Power Law Spectral Bias in the Learning Dynamics of Diffusion Models
Mar 05, 2025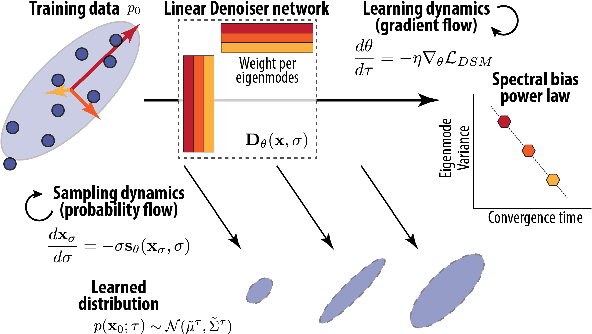

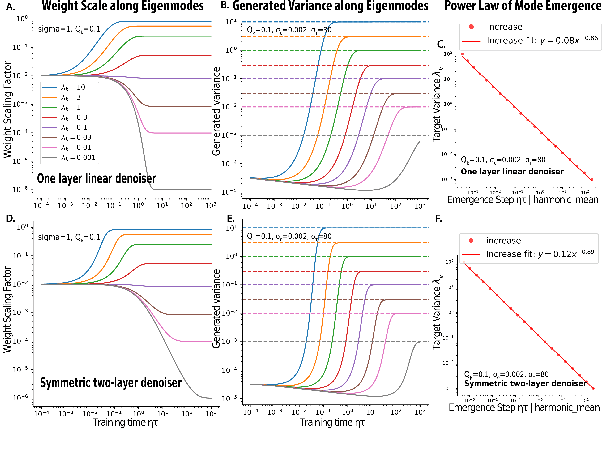
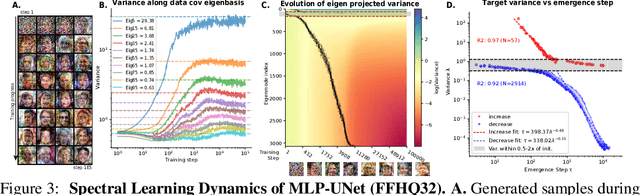
Abstract:We developed an analytical framework for understanding how the learned distribution evolves during diffusion model training. Leveraging the Gaussian equivalence principle, we derived exact solutions for the gradient-flow dynamics of weights in one- or two-layer linear denoiser settings with arbitrary data. Remarkably, these solutions allowed us to derive the generated distribution in closed form and its KL divergence through training. These analytical results expose a pronounced power-law spectral bias, i.e., for weights and distributions, the convergence time of a mode follows an inverse power law of its variance. Empirical experiments on both Gaussian and image datasets demonstrate that the power-law spectral bias remains robust even when using deeper or convolutional architectures. Our results underscore the importance of the data covariance in dictating the order and rate at which diffusion models learn different modes of the data, providing potential explanations for why earlier stopping could lead to incorrect details in image generative models.
Archetypal SAE: Adaptive and Stable Dictionary Learning for Concept Extraction in Large Vision Models
Feb 18, 2025Abstract:Sparse Autoencoders (SAEs) have emerged as a powerful framework for machine learning interpretability, enabling the unsupervised decomposition of model representations into a dictionary of abstract, human-interpretable concepts. However, we reveal a fundamental limitation: existing SAEs exhibit severe instability, as identical models trained on similar datasets can produce sharply different dictionaries, undermining their reliability as an interpretability tool. To address this issue, we draw inspiration from the Archetypal Analysis framework introduced by Cutler & Breiman (1994) and present Archetypal SAEs (A-SAE), wherein dictionary atoms are constrained to the convex hull of data. This geometric anchoring significantly enhances the stability of inferred dictionaries, and their mildly relaxed variants RA-SAEs further match state-of-the-art reconstruction abilities. To rigorously assess dictionary quality learned by SAEs, we introduce two new benchmarks that test (i) plausibility, if dictionaries recover "true" classification directions and (ii) identifiability, if dictionaries disentangle synthetic concept mixtures. Across all evaluations, RA-SAEs consistently yield more structured representations while uncovering novel, semantically meaningful concepts in large-scale vision models.
The Unreasonable Effectiveness of Gaussian Score Approximation for Diffusion Models and its Applications
Dec 12, 2024
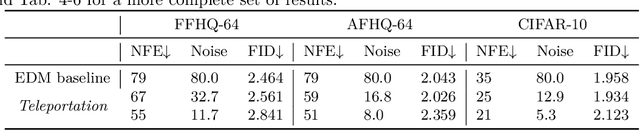
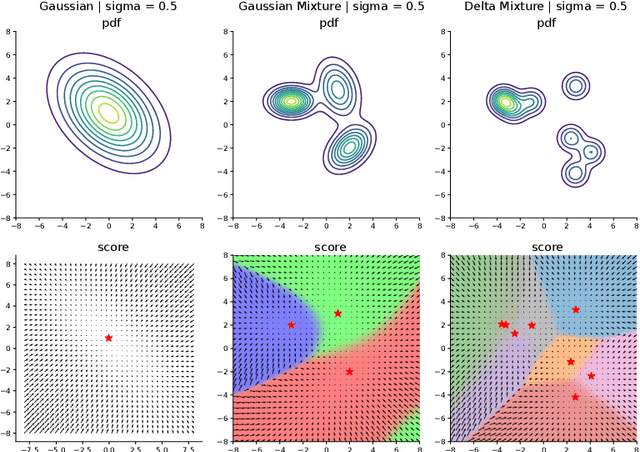

Abstract:By learning the gradient of smoothed data distributions, diffusion models can iteratively generate samples from complex distributions. The learned score function enables their generalization capabilities, but how the learned score relates to the score of the underlying data manifold remains largely unclear. Here, we aim to elucidate this relationship by comparing learned neural scores to the scores of two kinds of analytically tractable distributions: Gaussians and Gaussian mixtures. The simplicity of the Gaussian model makes it theoretically attractive, and we show that it admits a closed-form solution and predicts many qualitative aspects of sample generation dynamics. We claim that the learned neural score is dominated by its linear (Gaussian) approximation for moderate to high noise scales, and supply both theoretical and empirical arguments to support this claim. Moreover, the Gaussian approximation empirically works for a larger range of noise scales than naive theory suggests it should, and is preferentially learned early in training. At smaller noise scales, we observe that learned scores are better described by a coarse-grained (Gaussian mixture) approximation of training data than by the score of the training distribution, a finding consistent with generalization. Our findings enable us to precisely predict the initial phase of trained models' sampling trajectories through their Gaussian approximations. We show that this allows the skipping of the first 15-30% of sampling steps while maintaining high sample quality (with a near state-of-the-art FID score of 1.93 on CIFAR-10 unconditional generation). This forms the foundation of a novel hybrid sampling method, termed analytical teleportation, which can seamlessly integrate with and accelerate existing samplers, including DPM-Solver-v3 and UniPC. Our findings suggest ways to improve the design and training of diffusion models.
* 69 pages, 34 figures. Published in TMLR. Previous shorter versions at arxiv.org/abs/2303.02490 and arxiv.org/abs/2311.10892
Diverse capability and scaling of diffusion and auto-regressive models when learning abstract rules
Nov 12, 2024



Abstract:Humans excel at discovering regular structures from limited samples and applying inferred rules to novel settings. We investigate whether modern generative models can similarly learn underlying rules from finite samples and perform reasoning through conditional sampling. Inspired by Raven's Progressive Matrices task, we designed GenRAVEN dataset, where each sample consists of three rows, and one of 40 relational rules governing the object position, number, or attributes applies to all rows. We trained generative models to learn the data distribution, where samples are encoded as integer arrays to focus on rule learning. We compared two generative model families: diffusion (EDM, DiT, SiT) and autoregressive models (GPT2, Mamba). We evaluated their ability to generate structurally consistent samples and perform panel completion via unconditional and conditional sampling. We found diffusion models excel at unconditional generation, producing more novel and consistent samples from scratch and memorizing less, but performing less well in panel completion, even with advanced conditional sampling methods. Conversely, autoregressive models excel at completing missing panels in a rule-consistent manner but generate less consistent samples unconditionally. We observe diverse data scaling behaviors: for both model families, rule learning emerges at a certain dataset size - around 1000s examples per rule. With more training data, diffusion models improve both their unconditional and conditional generation capabilities. However, for autoregressive models, while panel completion improves with more training data, unconditional generation consistency declines. Our findings highlight complementary capabilities and limitations of diffusion and autoregressive models in rule learning and reasoning tasks, suggesting avenues for further research into their mechanisms and potential for human-like reasoning.
The Hidden Linear Structure in Score-Based Models and its Application
Nov 17, 2023Abstract:Score-based models have achieved remarkable results in the generative modeling of many domains. By learning the gradient of smoothed data distribution, they can iteratively generate samples from complex distribution e.g. natural images. However, is there any universal structure in the gradient field that will eventually be learned by any neural network? Here, we aim to find such structures through a normative analysis of the score function. First, we derived the closed-form solution to the scored-based model with a Gaussian score. We claimed that for well-trained diffusion models, the learned score at a high noise scale is well approximated by the linear score of Gaussian. We demonstrated this through empirical validation of pre-trained images diffusion model and theoretical analysis of the score function. This finding enabled us to precisely predict the initial diffusion trajectory using the analytical solution and to accelerate image sampling by 15-30\% by skipping the initial phase without sacrificing image quality. Our finding of the linear structure in the score-based model has implications for better model design and data pre-processing.
Diffusion Models Generate Images Like Painters: an Analytical Theory of Outline First, Details Later
Mar 04, 2023

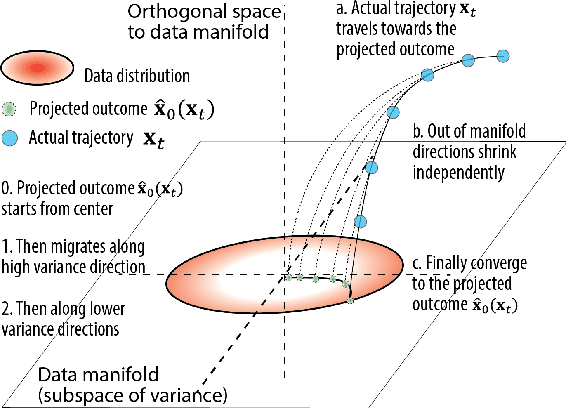
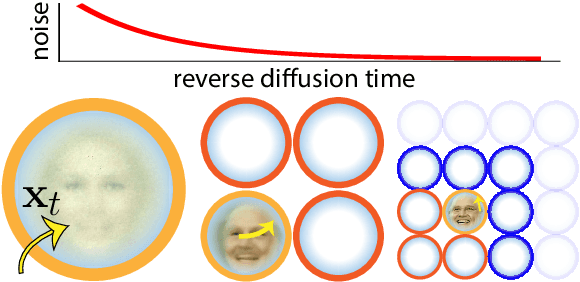
Abstract:How do diffusion generative models convert pure noise into meaningful images? We argue that generation involves first committing to an outline, and then to finer and finer details. The corresponding reverse diffusion process can be modeled by dynamics on a (time-dependent) high-dimensional landscape full of Gaussian-like modes, which makes the following predictions: (i) individual trajectories tend to be very low-dimensional; (ii) scene elements that vary more within training data tend to emerge earlier; and (iii) early perturbations substantially change image content more often than late perturbations. We show that the behavior of a variety of trained unconditional and conditional diffusion models like Stable Diffusion is consistent with these predictions. Finally, we use our theory to search for the latent image manifold of diffusion models, and propose a new way to generate interpretable image variations. Our viewpoint suggests generation by GANs and diffusion models have unexpected similarities.
On the Level Sets and Invariance of Neural Tuning Landscapes
Dec 26, 2022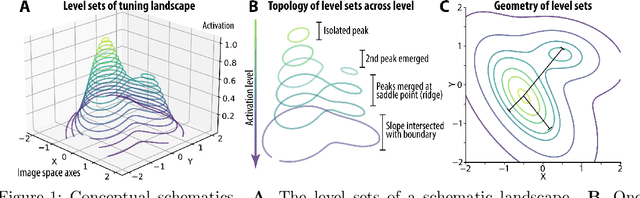
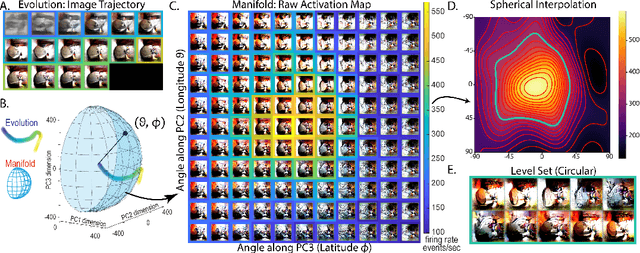
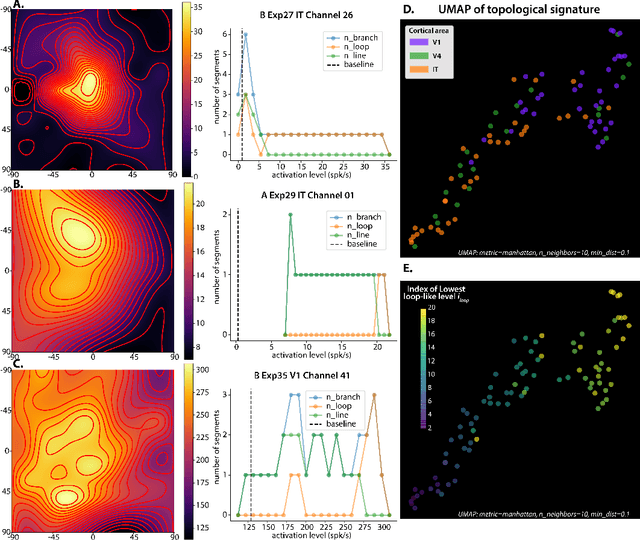

Abstract:Visual representations can be defined as the activations of neuronal populations in response to images. The activation of a neuron as a function over all image space has been described as a "tuning landscape". As a function over a high-dimensional space, what is the structure of this landscape? In this study, we characterize tuning landscapes through the lens of level sets and Morse theory. A recent study measured the in vivo two-dimensional tuning maps of neurons in different brain regions. Here, we developed a statistically reliable signature for these maps based on the change of topology in level sets. We found this topological signature changed progressively throughout the cortical hierarchy, with similar trends found for units in convolutional neural networks (CNNs). Further, we analyzed the geometry of level sets on the tuning landscapes of CNN units. We advanced the hypothesis that higher-order units can be locally regarded as isotropic radial basis functions, but not globally. This shows the power of level sets as a conceptual tool to understand neuronal activations over image space.
High-performance Evolutionary Algorithms for Online Neuron Control
Apr 14, 2022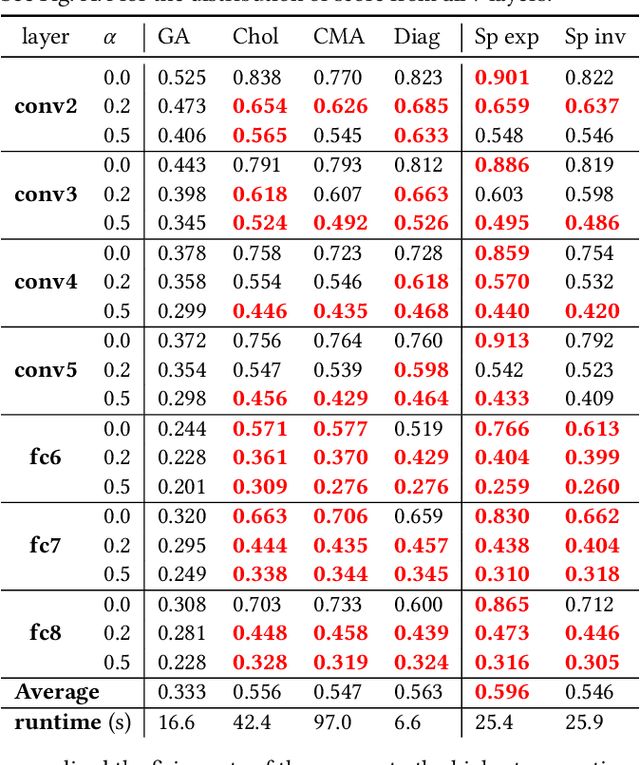

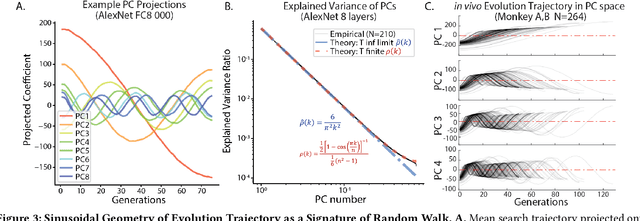

Abstract:Recently, optimization has become an emerging tool for neuroscientists to study neural code. In the visual system, neurons respond to images with graded and noisy responses. Image patterns eliciting highest responses are diagnostic of the coding content of the neuron. To find these patterns, we have used black-box optimizers to search a 4096d image space, leading to the evolution of images that maximize neuronal responses. Although genetic algorithm (GA) has been commonly used, there haven't been any systematic investigations to reveal the best performing optimizer or the underlying principles necessary to improve them. Here, we conducted a large scale in silico benchmark of optimizers for activation maximization and found that Covariance Matrix Adaptation (CMA) excelled in its achieved activation. We compared CMA against GA and found that CMA surpassed the maximal activation of GA by 66% in silico and 44% in vivo. We analyzed the structure of Evolution trajectories and found that the key to success was not covariance matrix adaptation, but local search towards informative dimensions and an effective step size decay. Guided by these principles and the geometry of the image manifold, we developed SphereCMA optimizer which competed well against CMA, proving the validity of the identified principles. Code available at https://github.com/Animadversio/ActMax-Optimizer-Dev
On the use of Cortical Magnification and Saccades as Biological Proxies for Data Augmentation
Dec 14, 2021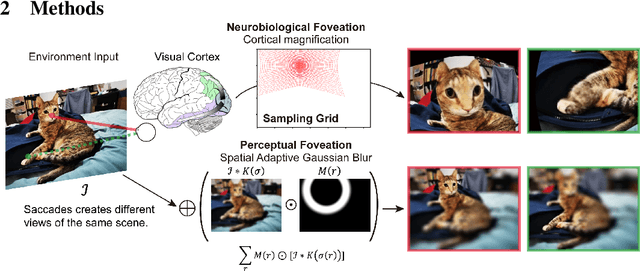
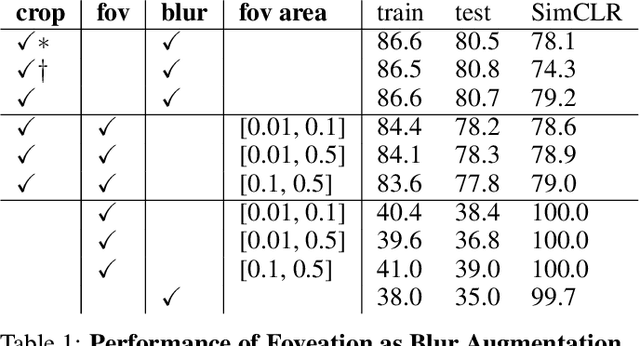
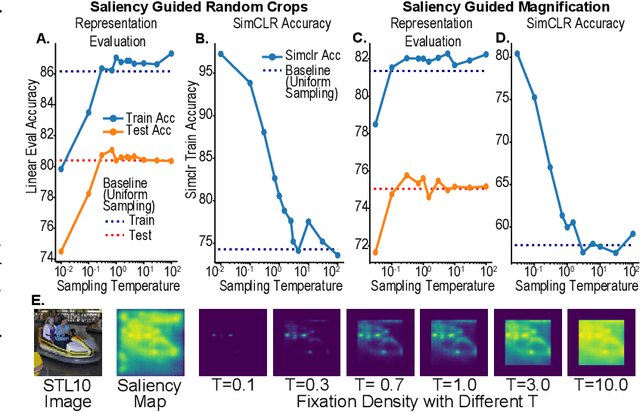
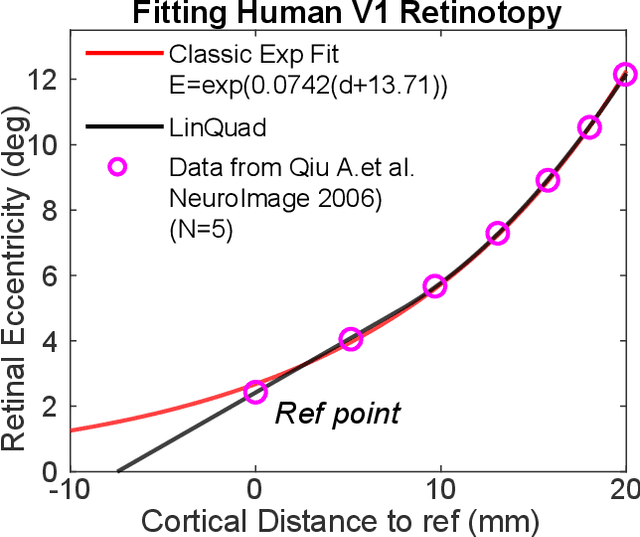
Abstract:Self-supervised learning is a powerful way to learn useful representations from natural data. It has also been suggested as one possible means of building visual representation in humans, but the specific objective and algorithm are unknown. Currently, most self-supervised methods encourage the system to learn an invariant representation of different transformations of the same image in contrast to those of other images. However, such transformations are generally non-biologically plausible, and often consist of contrived perceptual schemes such as random cropping and color jittering. In this paper, we attempt to reverse-engineer these augmentations to be more biologically or perceptually plausible while still conferring the same benefits for encouraging robust representation. Critically, we find that random cropping can be substituted by cortical magnification, and saccade-like sampling of the image could also assist the representation learning. The feasibility of these transformations suggests a potential way that biological visual systems could implement self-supervision. Further, they break the widely accepted spatially-uniform processing assumption used in many computer vision algorithms, suggesting a role for spatially-adaptive computation in humans and machines alike. Our code and demo can be found here.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge