Gradient Descent as Loss Landscape Navigation: a Normative Framework for Deriving Learning Rules

Learning rules -- prescriptions for updating model parameters to improve performance -- are typically assumed rather than derived. Why do some learning rules work better than others, and under what assumptions can a given rule be considered optimal? We propose a theoretical framework that casts learning rules as policies for navigating (partially observable) loss landscapes, and identifies optimal rules as solutions to an associated optimal control problem. A range of well-known rules emerge naturally within this framework under different assumptions: gradient descent from short-horizon optimization, momentum from longer-horizon planning, natural gradients from accounting for parameter space geometry, non-gradient rules from partial controllability, and adaptive optimizers like Adam from online Bayesian inference of loss landscape shape. We further show that continual learning strategies like weight resetting can be understood as optimal responses to task uncertainty. By unifying these phenomena under a single objective, our framework clarifies the computational structure of learning and offers a principled foundation for designing adaptive algorithms.

Deep RL Needs Deep Behavior Analysis: Exploring Implicit Planning by Model-Free Agents in Open-Ended Environments

Understanding the behavior of deep reinforcement learning (DRL) agents -- particularly as task and agent sophistication increase -- requires more than simple comparison of reward curves, yet standard methods for behavioral analysis remain underdeveloped in DRL. We apply tools from neuroscience and ethology to study DRL agents in a novel, complex, partially observable environment, ForageWorld, designed to capture key aspects of real-world animal foraging -- including sparse, depleting resource patches, predator threats, and spatially extended arenas. We use this environment as a platform for applying joint behavioral and neural analysis to agents, revealing detailed, quantitatively grounded insights into agent strategies, memory, and planning. Contrary to common assumptions, we find that model-free RNN-based DRL agents can exhibit structured, planning-like behavior purely through emergent dynamics -- without requiring explicit memory modules or world models. Our results show that studying DRL agents like animals -- analyzing them with neuroethology-inspired tools that reveal structure in both behavior and neural dynamics -- uncovers rich structure in their learning dynamics that would otherwise remain invisible. We distill these tools into a general analysis framework linking core behavioral and representational features to diagnostic methods, which can be reused for a wide range of tasks and agents. As agents grow more complex and autonomous, bridging neuroscience, cognitive science, and AI will be essential -- not just for understanding their behavior, but for ensuring safe alignment and maximizing desirable behaviors that are hard to measure via reward. We show how this can be done by drawing on lessons from how biological intelligence is studied.

Generalization through variance: how noise shapes inductive biases in diffusion models

How diffusion models generalize beyond their training set is not known, and is somewhat mysterious given two facts: the optimum of the denoising score matching (DSM) objective usually used to train diffusion models is the score function of the training distribution; and the networks usually used to learn the score function are expressive enough to learn this score to high accuracy. We claim that a certain feature of the DSM objective -- the fact that its target is not the training distribution's score, but a noisy quantity only equal to it in expectation -- strongly impacts whether and to what extent diffusion models generalize. In this paper, we develop a mathematical theory that partly explains this 'generalization through variance' phenomenon. Our theoretical analysis exploits a physics-inspired path integral approach to compute the distributions typically learned by a few paradigmatic under- and overparameterized diffusion models. We find that the distributions diffusion models effectively learn to sample from resemble their training distributions, but with 'gaps' filled in, and that this inductive bias is due to the covariance structure of the noisy target used during training. We also characterize how this inductive bias interacts with feature-related inductive biases.

Dynamical symmetries in the fluctuation-driven regime: an application of Noether's theorem to noisy dynamical systems

Noether's theorem provides a powerful link between continuous symmetries and conserved quantities for systems governed by some variational principle. Perhaps unfortunately, most dynamical systems of interest in neuroscience and artificial intelligence cannot be described by any such principle. On the other hand, nonequilibrium physics provides a variational principle that describes how fairly generic noisy dynamical systems are most likely to transition between two states; in this work, we exploit this principle to apply Noether's theorem, and hence learn about how the continuous symmetries of dynamical systems constrain their most likely trajectories. We identify analogues of the conservation of energy, momentum, and angular momentum, and briefly discuss examples of each in the context of models of decision-making, recurrent neural networks, and diffusion generative models.

The Unreasonable Effectiveness of Gaussian Score Approximation for Diffusion Models and its Applications

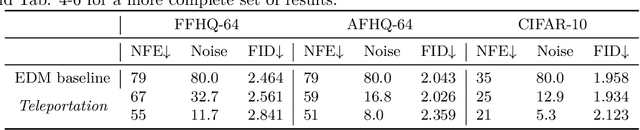
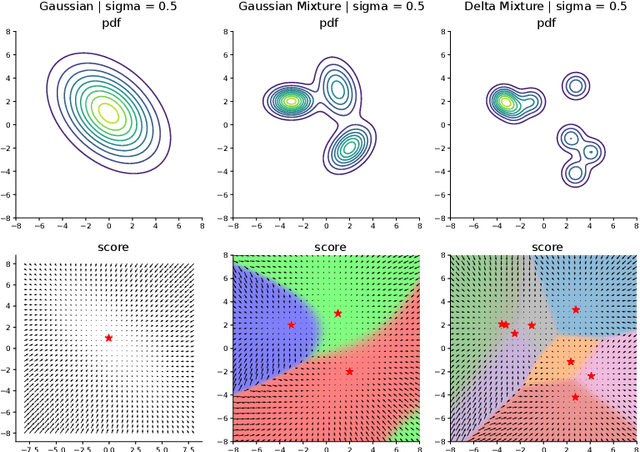
By learning the gradient of smoothed data distributions, diffusion models can iteratively generate samples from complex distributions. The learned score function enables their generalization capabilities, but how the learned score relates to the score of the underlying data manifold remains largely unclear. Here, we aim to elucidate this relationship by comparing learned neural scores to the scores of two kinds of analytically tractable distributions: Gaussians and Gaussian mixtures. The simplicity of the Gaussian model makes it theoretically attractive, and we show that it admits a closed-form solution and predicts many qualitative aspects of sample generation dynamics. We claim that the learned neural score is dominated by its linear (Gaussian) approximation for moderate to high noise scales, and supply both theoretical and empirical arguments to support this claim. Moreover, the Gaussian approximation empirically works for a larger range of noise scales than naive theory suggests it should, and is preferentially learned early in training. At smaller noise scales, we observe that learned scores are better described by a coarse-grained (Gaussian mixture) approximation of training data than by the score of the training distribution, a finding consistent with generalization. Our findings enable us to precisely predict the initial phase of trained models' sampling trajectories through their Gaussian approximations. We show that this allows the skipping of the first 15-30% of sampling steps while maintaining high sample quality (with a near state-of-the-art FID score of 1.93 on CIFAR-10 unconditional generation). This forms the foundation of a novel hybrid sampling method, termed analytical teleportation, which can seamlessly integrate with and accelerate existing samplers, including DPM-Solver-v3 and UniPC. Our findings suggest ways to improve the design and training of diffusion models.

The Hidden Linear Structure in Score-Based Models and its Application

Score-based models have achieved remarkable results in the generative modeling of many domains. By learning the gradient of smoothed data distribution, they can iteratively generate samples from complex distribution e.g. natural images. However, is there any universal structure in the gradient field that will eventually be learned by any neural network? Here, we aim to find such structures through a normative analysis of the score function. First, we derived the closed-form solution to the scored-based model with a Gaussian score. We claimed that for well-trained diffusion models, the learned score at a high noise scale is well approximated by the linear score of Gaussian. We demonstrated this through empirical validation of pre-trained images diffusion model and theoretical analysis of the score function. This finding enabled us to precisely predict the initial diffusion trajectory using the analytical solution and to accelerate image sampling by 15-30\% by skipping the initial phase without sacrificing image quality. Our finding of the linear structure in the score-based model has implications for better model design and data pre-processing.

Diffusion Models Generate Images Like Painters: an Analytical Theory of Outline First, Details Later

How do diffusion generative models convert pure noise into meaningful images? We argue that generation involves first committing to an outline, and then to finer and finer details. The corresponding reverse diffusion process can be modeled by dynamics on a (time-dependent) high-dimensional landscape full of Gaussian-like modes, which makes the following predictions: (i) individual trajectories tend to be very low-dimensional; (ii) scene elements that vary more within training data tend to emerge earlier; and (iii) early perturbations substantially change image content more often than late perturbations. We show that the behavior of a variety of trained unconditional and conditional diffusion models like Stable Diffusion is consistent with these predictions. Finally, we use our theory to search for the latent image manifold of diffusion models, and propose a new way to generate interpretable image variations. Our viewpoint suggests generation by GANs and diffusion models have unexpected similarities.