On the Level Sets and Invariance of Neural Tuning Landscapes

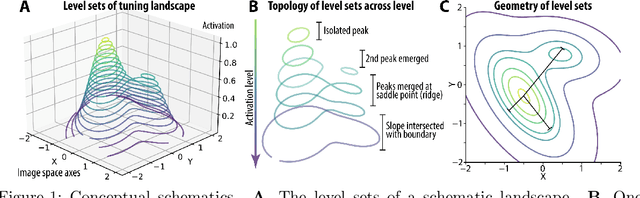
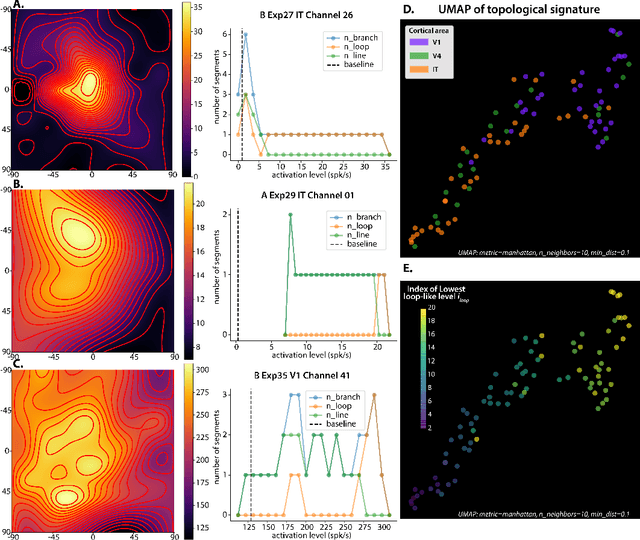
Visual representations can be defined as the activations of neuronal populations in response to images. The activation of a neuron as a function over all image space has been described as a "tuning landscape". As a function over a high-dimensional space, what is the structure of this landscape? In this study, we characterize tuning landscapes through the lens of level sets and Morse theory. A recent study measured the in vivo two-dimensional tuning maps of neurons in different brain regions. Here, we developed a statistically reliable signature for these maps based on the change of topology in level sets. We found this topological signature changed progressively throughout the cortical hierarchy, with similar trends found for units in convolutional neural networks (CNNs). Further, we analyzed the geometry of level sets on the tuning landscapes of CNN units. We advanced the hypothesis that higher-order units can be locally regarded as isotropic radial basis functions, but not globally. This shows the power of level sets as a conceptual tool to understand neuronal activations over image space.

High-performance Evolutionary Algorithms for Online Neuron Control

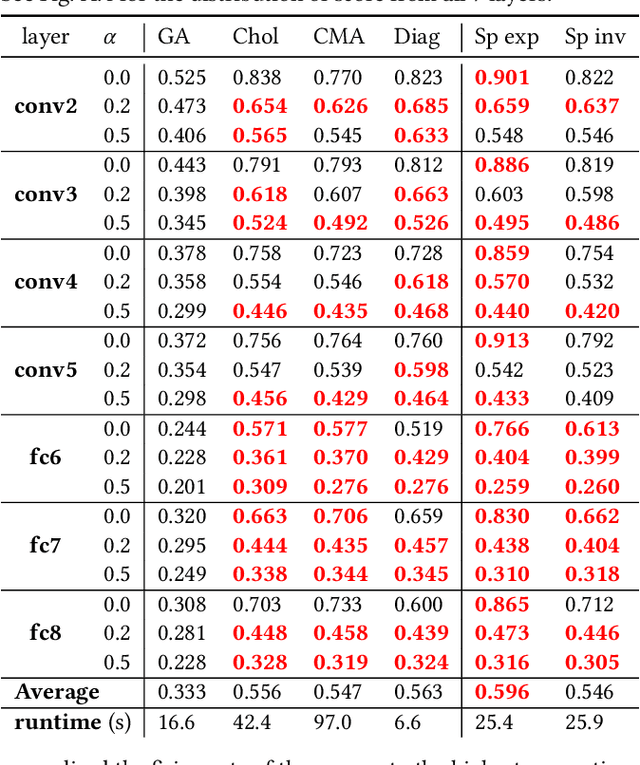
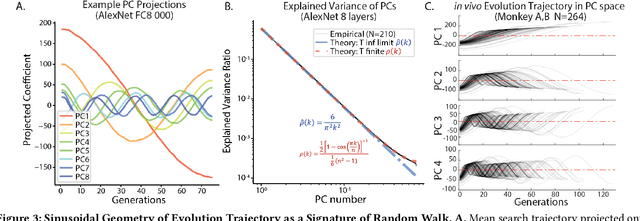
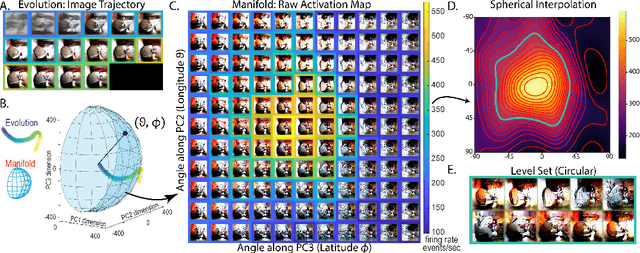
Recently, optimization has become an emerging tool for neuroscientists to study neural code. In the visual system, neurons respond to images with graded and noisy responses. Image patterns eliciting highest responses are diagnostic of the coding content of the neuron. To find these patterns, we have used black-box optimizers to search a 4096d image space, leading to the evolution of images that maximize neuronal responses. Although genetic algorithm (GA) has been commonly used, there haven't been any systematic investigations to reveal the best performing optimizer or the underlying principles necessary to improve them. Here, we conducted a large scale in silico benchmark of optimizers for activation maximization and found that Covariance Matrix Adaptation (CMA) excelled in its achieved activation. We compared CMA against GA and found that CMA surpassed the maximal activation of GA by 66% in silico and 44% in vivo. We analyzed the structure of Evolution trajectories and found that the key to success was not covariance matrix adaptation, but local search towards informative dimensions and an effective step size decay. Guided by these principles and the geometry of the image manifold, we developed SphereCMA optimizer which competed well against CMA, proving the validity of the identified principles. Code available at https://github.com/Animadversio/ActMax-Optimizer-Dev

The Geometry of Deep Generative Image Models and its Applications

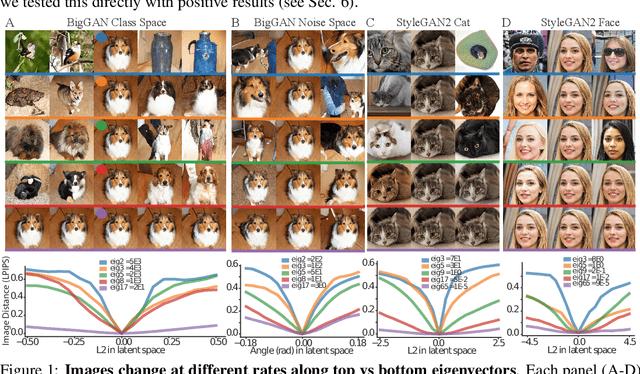
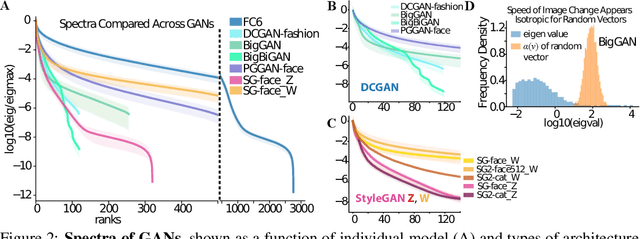
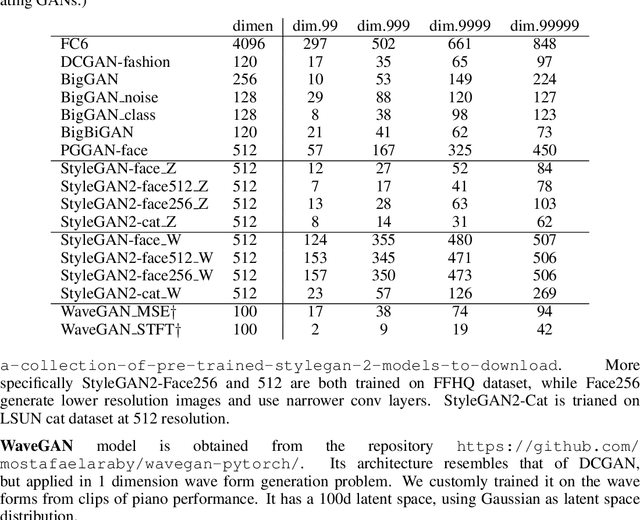
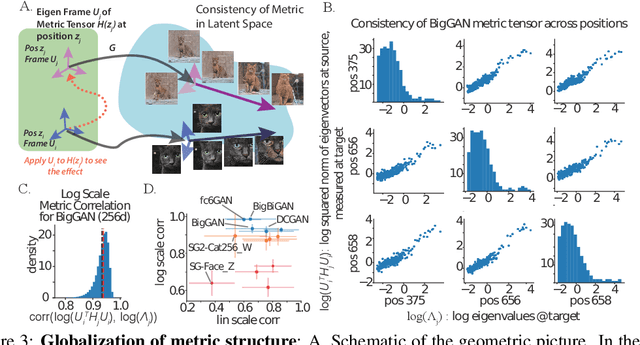
Generative adversarial networks (GANs) have emerged as a powerful unsupervised method to model the statistical patterns of real-world data sets, such as natural images. These networks are trained to map random inputs in their latent space to new samples representative of the learned data. However, the structure of the latent space is hard to intuit due to its high dimensionality and the non-linearity of the generator, which limits the usefulness of the models. Understanding the latent space requires a way to identify input codes for existing real-world images (inversion), and a way to identify directions with known image transformations (interpretability). Here, we use a geometric framework to address both issues simultaneously. We develop an architecture-agnostic method to compute the Riemannian metric of the image manifold created by GANs. The eigen-decomposition of the metric isolates axes that account for different levels of image variability. An empirical analysis of several pretrained GANs shows that image variation around each position is concentrated along surprisingly few major axes (the space is highly anisotropic) and the directions that create this large variation are similar at different positions in the space (the space is homogeneous). We show that many of the top eigenvectors correspond to interpretable transforms in the image space, with a substantial part of eigenspace corresponding to minor transforms which could be compressed out. This geometric understanding unifies key previous results related to GAN interpretability. We show that the use of this metric allows for more efficient optimization in the latent space (e.g. GAN inversion) and facilitates unsupervised discovery of interpretable axes. Our results illustrate that defining the geometry of the GAN image manifold can serve as a general framework for understanding GANs.