Memorization and Knowledge Injection in Gated LLMs

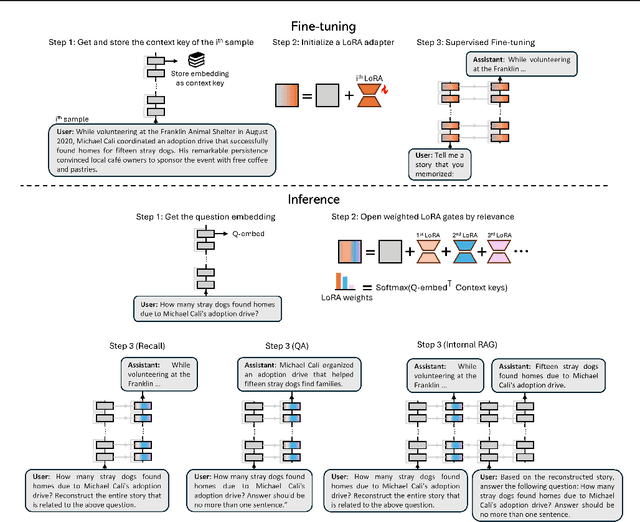
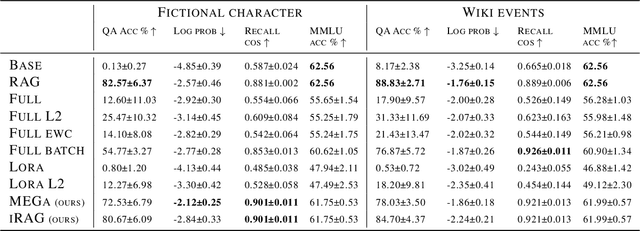
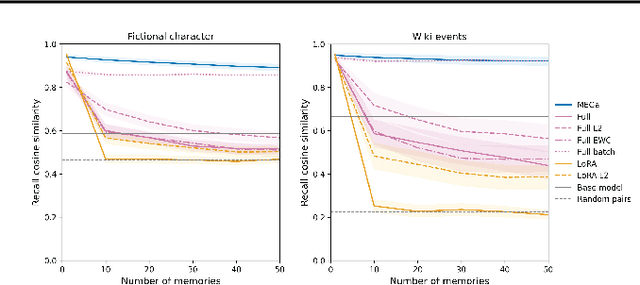
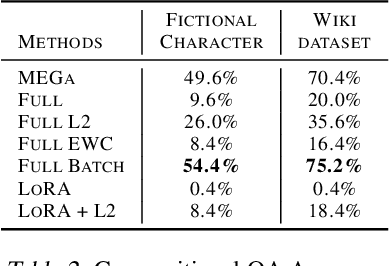
Large Language Models (LLMs) currently struggle to sequentially add new memories and integrate new knowledge. These limitations contrast with the human ability to continuously learn from new experiences and acquire knowledge throughout life. Most existing approaches add memories either through large context windows or external memory buffers (e.g., Retrieval-Augmented Generation), and studies on knowledge injection rarely test scenarios resembling everyday life events. In this work, we introduce a continual learning framework, Memory Embedded in Gated LLMs (MEGa), which injects event memories directly into the weights of LLMs. Each memory is stored in a dedicated set of gated low-rank weights. During inference, a gating mechanism activates relevant memory weights by matching query embeddings to stored memory embeddings. This enables the model to both recall entire memories and answer related questions. On two datasets - fictional characters and Wikipedia events - MEGa outperforms baseline approaches in mitigating catastrophic forgetting. Our model draws inspiration from the complementary memory system of the human brain.

Unraveling the geometry of visual relational reasoning

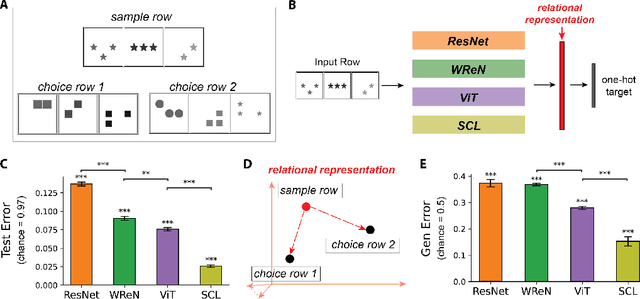
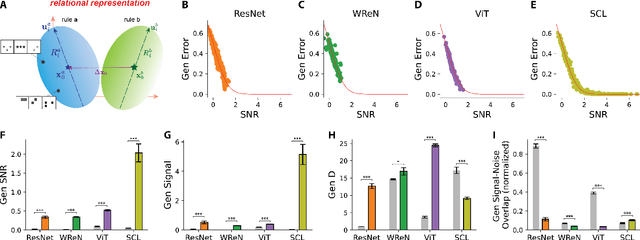
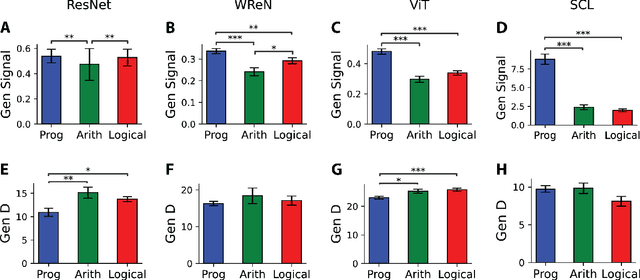
Humans and other animals readily generalize abstract relations, such as recognizing constant in shape or color, whereas neural networks struggle. To investigate how neural networks generalize abstract relations, we introduce SimplifiedRPM, a novel benchmark for systematic evaluation. In parallel, we conduct human experiments to benchmark relational difficulty, enabling direct model-human comparisons. Testing four architectures--ResNet-50, Vision Transformer, Wild Relation Network, and Scattering Compositional Learner (SCL)--we find that SCL best aligns with human behavior and generalizes best. Building on a geometric theory of neural representations, we show representational geometries that predict generalization. Layer-wise analysis reveals distinct relational reasoning strategies across models and suggests a trade-off where unseen rule representations compress into training-shaped subspaces. Guided by our geometric perspective, we propose and evaluate SNRloss, a novel objective balancing representation geometry. Our findings offer geometric insights into how neural networks generalize abstract relations, paving the way for more human-like visual reasoning in AI.

Simplified derivations for high-dimensional convex learning problems

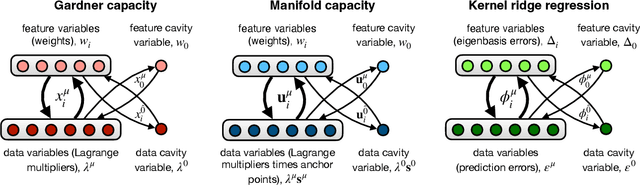
Statistical physics provides tools for analyzing high-dimensional problems in machine learning and theoretical neuroscience. These calculations, particularly those using the replica method, often involve lengthy derivations that can obscure physical interpretation. We give concise, non-replica derivations of several key results and highlight their underlying similarities. Specifically, we introduce a cavity approach to analyzing high-dimensional learning problems and apply it to three cases: perceptron classification of points, perceptron classification of manifolds, and kernel ridge regression. These problems share a common structure -- a bipartite system of interacting feature and datum variables -- enabling a unified analysis. For perceptron-capacity problems, we identify a symmetry that allows derivation of correct capacities through a na\"ive method. These results match those obtained through the replica method.

Diverse capability and scaling of diffusion and auto-regressive models when learning abstract rules

Humans excel at discovering regular structures from limited samples and applying inferred rules to novel settings. We investigate whether modern generative models can similarly learn underlying rules from finite samples and perform reasoning through conditional sampling. Inspired by Raven's Progressive Matrices task, we designed GenRAVEN dataset, where each sample consists of three rows, and one of 40 relational rules governing the object position, number, or attributes applies to all rows. We trained generative models to learn the data distribution, where samples are encoded as integer arrays to focus on rule learning. We compared two generative model families: diffusion (EDM, DiT, SiT) and autoregressive models (GPT2, Mamba). We evaluated their ability to generate structurally consistent samples and perform panel completion via unconditional and conditional sampling. We found diffusion models excel at unconditional generation, producing more novel and consistent samples from scratch and memorizing less, but performing less well in panel completion, even with advanced conditional sampling methods. Conversely, autoregressive models excel at completing missing panels in a rule-consistent manner but generate less consistent samples unconditionally. We observe diverse data scaling behaviors: for both model families, rule learning emerges at a certain dataset size - around 1000s examples per rule. With more training data, diffusion models improve both their unconditional and conditional generation capabilities. However, for autoregressive models, while panel completion improves with more training data, unconditional generation consistency declines. Our findings highlight complementary capabilities and limitations of diffusion and autoregressive models in rule learning and reasoning tasks, suggesting avenues for further research into their mechanisms and potential for human-like reasoning.

Robust Learning in Bayesian Parallel Branching Graph Neural Networks: The Narrow Width Limit

The infinite width limit of random neural networks is known to result in Neural Networks as Gaussian Process (NNGP) (Lee et al. [2018]), characterized by task-independent kernels. It is widely accepted that larger network widths contribute to improved generalization (Park et al. [2019]). However, this work challenges this notion by investigating the narrow width limit of the Bayesian Parallel Branching Graph Neural Network (BPB-GNN), an architecture that resembles residual networks. We demonstrate that when the width of a BPB-GNN is significantly smaller compared to the number of training examples, each branch exhibits more robust learning due to a symmetry breaking of branches in kernel renormalization. Surprisingly, the performance of a BPB-GNN in the narrow width limit is generally superior or comparable to that achieved in the wide width limit in bias-limited scenarios. Furthermore, the readout norms of each branch in the narrow width limit are mostly independent of the architectural hyperparameters but generally reflective of the nature of the data. Our results characterize a newly defined narrow-width regime for parallel branching networks in general.

Order parameters and phase transitions of continual learning in deep neural networks

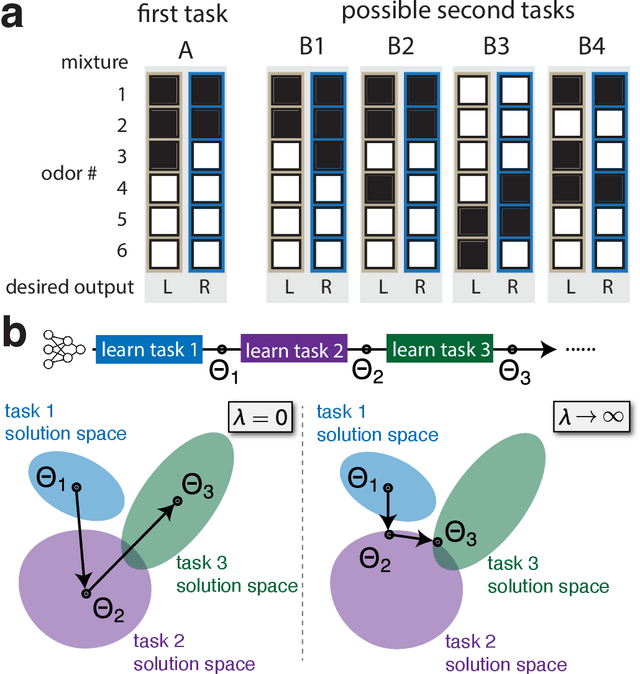
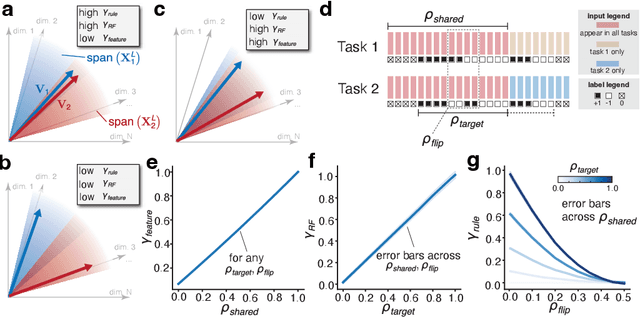
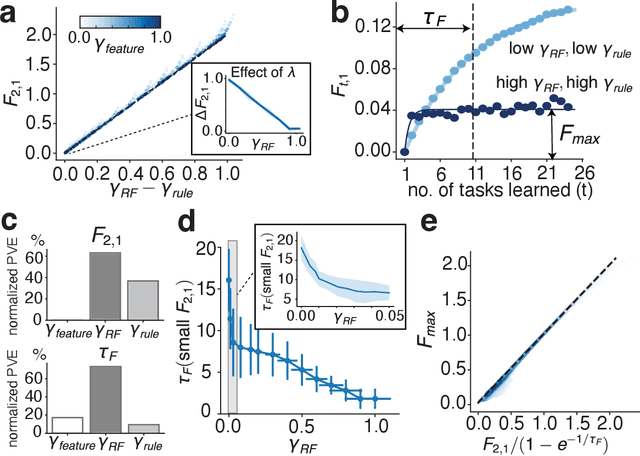
Continual learning (CL) enables animals to learn new tasks without erasing prior knowledge. CL in artificial neural networks (NNs) is challenging due to catastrophic forgetting, where new learning degrades performance on older tasks. While various techniques exist to mitigate forgetting, theoretical insights into when and why CL fails in NNs are lacking. Here, we present a statistical-mechanics theory of CL in deep, wide NNs, which characterizes the network's input-output mapping as it learns a sequence of tasks. It gives rise to order parameters (OPs) that capture how task relations and network architecture influence forgetting and knowledge transfer, as verified by numerical evaluations. We found that the input and rule similarity between tasks have different effects on CL performance. In addition, the theory predicts that increasing the network depth can effectively reduce overlap between tasks, thereby lowering forgetting. For networks with task-specific readouts, the theory identifies a phase transition where CL performance shifts dramatically as tasks become less similar, as measured by the OPs. Sufficiently low similarity leads to catastrophic anterograde interference, where the network retains old tasks perfectly but completely fails to generalize new learning. Our results delineate important factors affecting CL performance and suggest strategies for mitigating forgetting.

Coding schemes in neural networks learning classification tasks

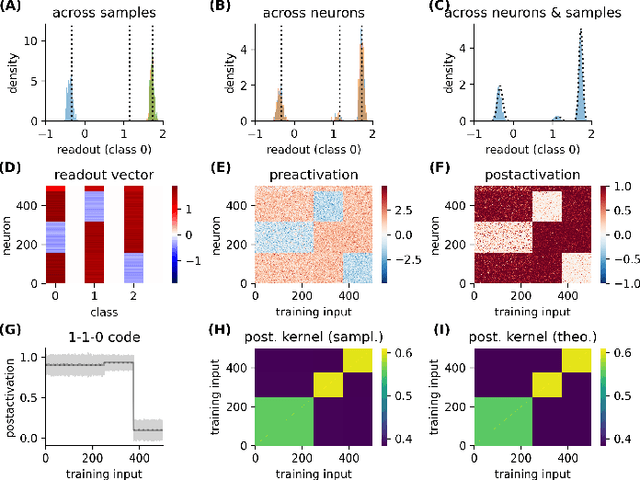
Neural networks posses the crucial ability to generate meaningful representations of task-dependent features. Indeed, with appropriate scaling, supervised learning in neural networks can result in strong, task-dependent feature learning. However, the nature of the emergent representations, which we call the `coding scheme', is still unclear. To understand the emergent coding scheme, we investigate fully-connected, wide neural networks learning classification tasks using the Bayesian framework where learning shapes the posterior distribution of the network weights. Consistent with previous findings, our analysis of the feature learning regime (also known as `non-lazy', `rich', or `mean-field' regime) shows that the networks acquire strong, data-dependent features. Surprisingly, the nature of the internal representations depends crucially on the neuronal nonlinearity. In linear networks, an analog coding scheme of the task emerges. Despite the strong representations, the mean predictor is identical to the lazy case. In nonlinear networks, spontaneous symmetry breaking leads to either redundant or sparse coding schemes. Our findings highlight how network properties such as scaling of weights and neuronal nonlinearity can profoundly influence the emergent representations.

Dissecting the Interplay of Attention Paths in a Statistical Mechanics Theory of Transformers

Despite the remarkable empirical performance of Transformers, their theoretical understanding remains elusive. Here, we consider a deep multi-head self-attention network, that is closely related to Transformers yet analytically tractable. We develop a statistical mechanics theory of Bayesian learning in this model, deriving exact equations for the network's predictor statistics under the finite-width thermodynamic limit, i.e., $N,P\rightarrow\infty$, $P/N=\mathcal{O}(1)$, where $N$ is the network width and $P$ is the number of training examples. Our theory shows that the predictor statistics are expressed as a sum of independent kernels, each one pairing different 'attention paths', defined as information pathways through different attention heads across layers. The kernels are weighted according to a 'task-relevant kernel combination' mechanism that aligns the total kernel with the task labels. As a consequence, this interplay between attention paths enhances generalization performance. Experiments confirm our findings on both synthetic and real-world sequence classification tasks. Finally, our theory explicitly relates the kernel combination mechanism to properties of the learned weights, allowing for a qualitative transfer of its insights to models trained via gradient descent. As an illustration, we demonstrate an efficient size reduction of the network, by pruning those attention heads that are deemed less relevant by our theory.

Probing Biological and Artificial Neural Networks with Task-dependent Neural Manifolds

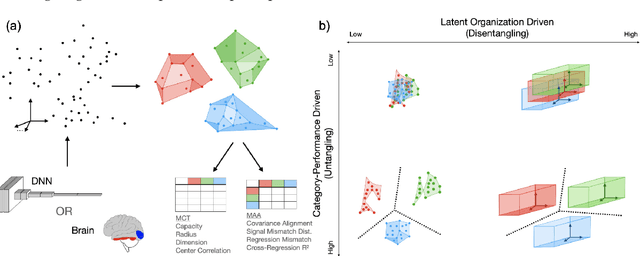
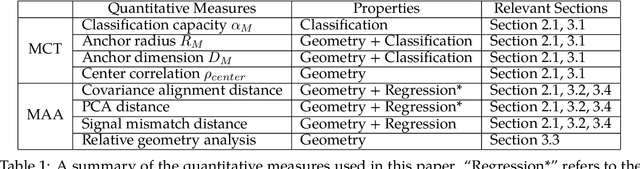
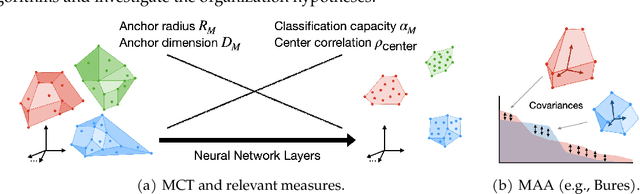
Recently, growth in our understanding of the computations performed in both biological and artificial neural networks has largely been driven by either low-level mechanistic studies or global normative approaches. However, concrete methodologies for bridging the gap between these levels of abstraction remain elusive. In this work, we investigate the internal mechanisms of neural networks through the lens of neural population geometry, aiming to provide understanding at an intermediate level of abstraction, as a way to bridge that gap. Utilizing manifold capacity theory (MCT) from statistical physics and manifold alignment analysis (MAA) from high-dimensional statistics, we probe the underlying organization of task-dependent manifolds in deep neural networks and macaque neural recordings. Specifically, we quantitatively characterize how different learning objectives lead to differences in the organizational strategies of these models and demonstrate how these geometric analyses are connected to the decodability of task-relevant information. These analyses present a strong direction for bridging mechanistic and normative theories in neural networks through neural population geometry, potentially opening up many future research avenues in both machine learning and neuroscience.

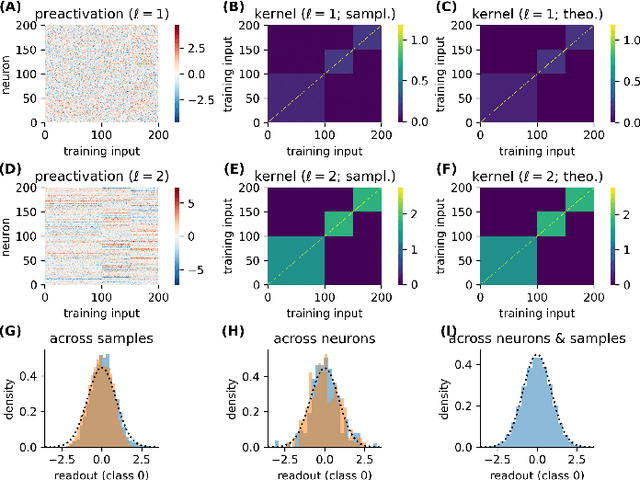
Connecting NTK and NNGP: A Unified Theoretical Framework for Neural Network Learning Dynamics in the Kernel Regime

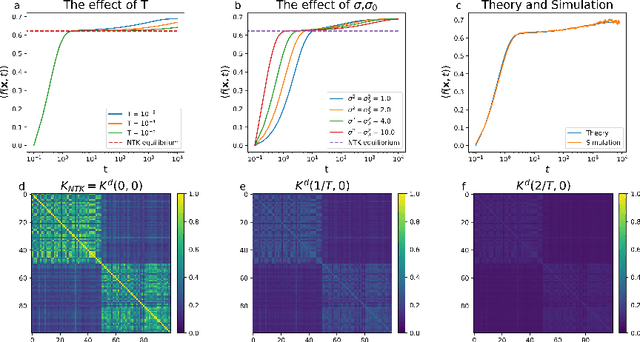
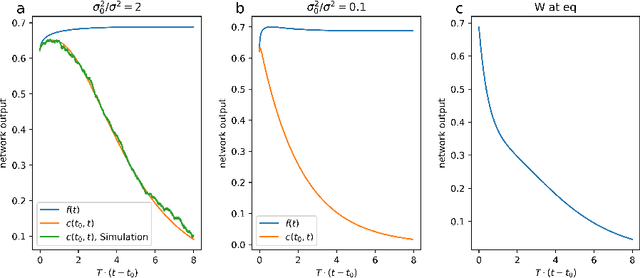
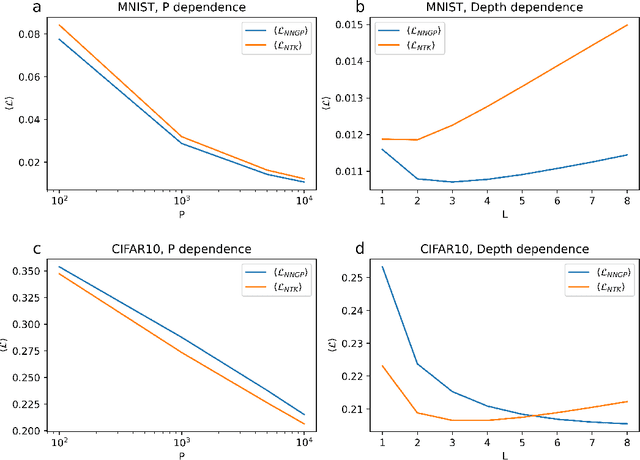
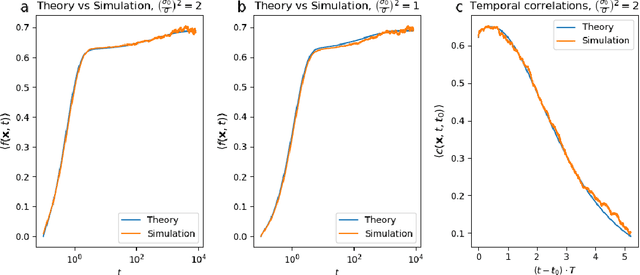
Artificial neural networks have revolutionized machine learning in recent years, but a complete theoretical framework for their learning process is still lacking. Substantial progress has been made for infinitely wide networks. In this regime, two disparate theoretical frameworks have been used, in which the network's output is described using kernels: one framework is based on the Neural Tangent Kernel (NTK) which assumes linearized gradient descent dynamics, while the Neural Network Gaussian Process (NNGP) kernel assumes a Bayesian framework. However, the relation between these two frameworks has remained elusive. This work unifies these two distinct theories using a Markov proximal learning model for learning dynamics in an ensemble of randomly initialized infinitely wide deep networks. We derive an exact analytical expression for the network input-output function during and after learning, and introduce a new time-dependent Neural Dynamical Kernel (NDK) from which both NTK and NNGP kernels can be derived. We identify two learning phases characterized by different time scales: gradient-driven and diffusive learning. In the initial gradient-driven learning phase, the dynamics is dominated by deterministic gradient descent, and is described by the NTK theory. This phase is followed by the diffusive learning stage, during which the network parameters sample the solution space, ultimately approaching the equilibrium distribution corresponding to NNGP. Combined with numerical evaluations on synthetic and benchmark datasets, we provide novel insights into the different roles of initialization, regularization, and network depth, as well as phenomena such as early stopping and representational drift. This work closes the gap between the NTK and NNGP theories, providing a comprehensive framework for understanding the learning process of deep neural networks in the infinite width limit.