Optimal Protocols for Continual Learning via Statistical Physics and Control Theory

Artificial neural networks often struggle with catastrophic forgetting when learning multiple tasks sequentially, as training on new tasks degrades the performance on previously learned ones. Recent theoretical work has addressed this issue by analysing learning curves in synthetic frameworks under predefined training protocols. However, these protocols relied on heuristics and lacked a solid theoretical foundation assessing their optimality. In this paper, we fill this gap combining exact equations for training dynamics, derived using statistical physics techniques, with optimal control methods. We apply this approach to teacher-student models for continual learning and multi-task problems, obtaining a theory for task-selection protocols maximising performance while minimising forgetting. Our theoretical analysis offers non-trivial yet interpretable strategies for mitigating catastrophic forgetting, shedding light on how optimal learning protocols can modulate established effects, such as the influence of task similarity on forgetting. Finally, we validate our theoretical findings on real-world data.

Dissecting the Interplay of Attention Paths in a Statistical Mechanics Theory of Transformers

Despite the remarkable empirical performance of Transformers, their theoretical understanding remains elusive. Here, we consider a deep multi-head self-attention network, that is closely related to Transformers yet analytically tractable. We develop a statistical mechanics theory of Bayesian learning in this model, deriving exact equations for the network's predictor statistics under the finite-width thermodynamic limit, i.e., $N,P\rightarrow\infty$, $P/N=\mathcal{O}(1)$, where $N$ is the network width and $P$ is the number of training examples. Our theory shows that the predictor statistics are expressed as a sum of independent kernels, each one pairing different 'attention paths', defined as information pathways through different attention heads across layers. The kernels are weighted according to a 'task-relevant kernel combination' mechanism that aligns the total kernel with the task labels. As a consequence, this interplay between attention paths enhances generalization performance. Experiments confirm our findings on both synthetic and real-world sequence classification tasks. Finally, our theory explicitly relates the kernel combination mechanism to properties of the learned weights, allowing for a qualitative transfer of its insights to models trained via gradient descent. As an illustration, we demonstrate an efficient size reduction of the network, by pruning those attention heads that are deemed less relevant by our theory.

Nonlinear classification of neural manifolds with contextual information

Understanding how neural systems efficiently process information through distributed representations is a fundamental challenge at the interface of neuroscience and machine learning. Recent approaches analyze the statistical and geometrical attributes of neural representations as population-level mechanistic descriptors of task implementation. In particular, manifold capacity has emerged as a promising framework linking population geometry to the separability of neural manifolds. However, this metric has been limited to linear readouts. Here, we propose a theoretical framework that overcomes this limitation by leveraging contextual input information. We derive an exact formula for the context-dependent capacity that depends on manifold geometry and context correlations, and validate it on synthetic and real data. Our framework's increased expressivity captures representation untanglement in deep networks at early stages of the layer hierarchy, previously inaccessible to analysis. As context-dependent nonlinearity is ubiquitous in neural systems, our data-driven and theoretically grounded approach promises to elucidate context-dependent computation across scales, datasets, and models.

Forward Learning with Top-Down Feedback: Empirical and Analytical Characterization

"Forward-only" algorithms, which train neural networks while avoiding a backward pass, have recently gained attention as a way of solving the biologically unrealistic aspects of backpropagation. Here, we first discuss the similarities between two "forward-only" algorithms, the Forward-Forward and PEPITA frameworks, and demonstrate that PEPITA is equivalent to a Forward-Forward with top-down feedback connections. Then, we focus on PEPITA to address compelling challenges related to the "forward-only" rules, which include providing an analytical understanding of their dynamics and reducing the gap between their performance and that of backpropagation. We propose a theoretical analysis of the dynamics of PEPITA. In particular, we show that PEPITA is well-approximated by an "adaptive-feedback-alignment" algorithm and we analytically track its performance during learning in a prototype high-dimensional setting. Finally, we develop a strategy to apply the weight mirroring algorithm on "forward-only" algorithms with top-down feedback and we show how it impacts PEPITA's accuracy and convergence rate.

Rigorous dynamical mean field theory for stochastic gradient descent methods

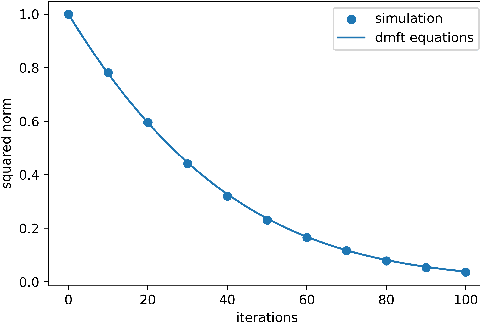
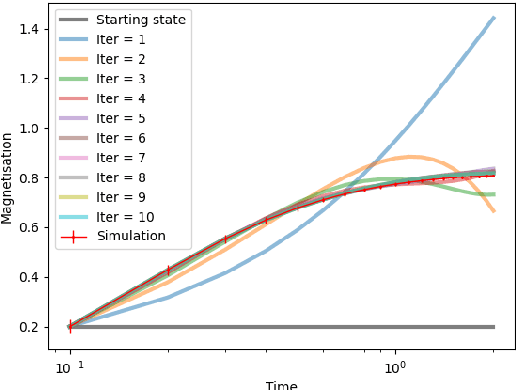
We prove closed-form equations for the exact high-dimensional asymptotics of a family of first order gradient-based methods, learning an estimator (e.g. M-estimator, shallow neural network, ...) from observations on Gaussian data with empirical risk minimization. This includes widely used algorithms such as stochastic gradient descent (SGD) or Nesterov acceleration. The obtained equations match those resulting from the discretization of dynamical mean-field theory (DMFT) equations from statistical physics when applied to gradient flow. Our proof method allows us to give an explicit description of how memory kernels build up in the effective dynamics, and to include non-separable update functions, allowing datasets with non-identity covariance matrices. Finally, we provide numerical implementations of the equations for SGD with generic extensive batch-size and with constant learning rates.

Learning curves for the multi-class teacher-student perceptron

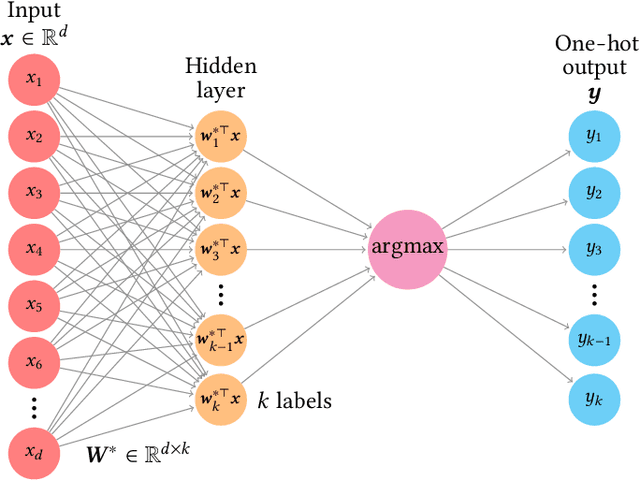
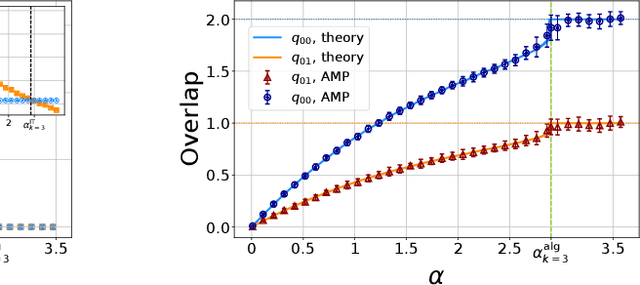
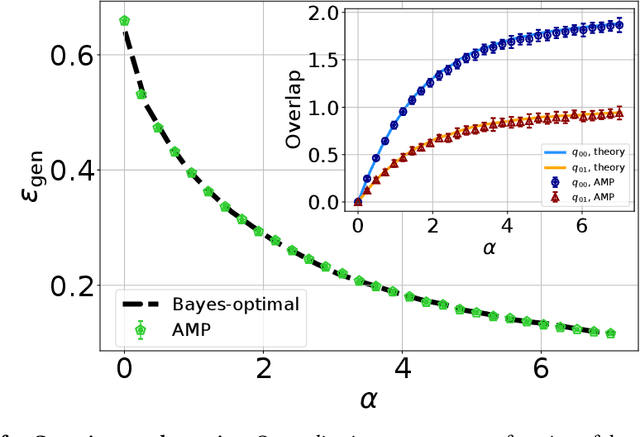
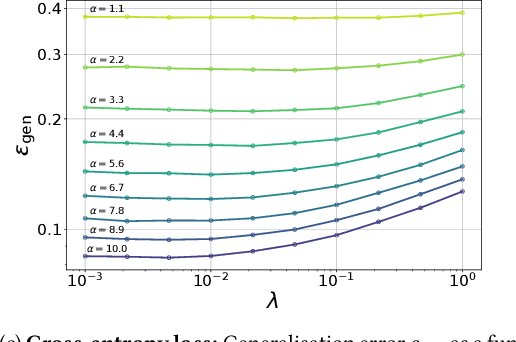
One of the most classical results in high-dimensional learning theory provides a closed-form expression for the generalisation error of binary classification with the single-layer teacher-student perceptron on i.i.d. Gaussian inputs. Both Bayes-optimal estimation and empirical risk minimisation (ERM) were extensively analysed for this setting. At the same time, a considerable part of modern machine learning practice concerns multi-class classification. Yet, an analogous analysis for the corresponding multi-class teacher-student perceptron was missing. In this manuscript we fill this gap by deriving and evaluating asymptotic expressions for both the Bayes-optimal and ERM generalisation errors in the high-dimensional regime. For Gaussian teacher weights, we investigate the performance of ERM with both cross-entropy and square losses, and explore the role of ridge regularisation in approaching Bayes-optimality. In particular, we observe that regularised cross-entropy minimisation yields close-to-optimal accuracy. Instead, for a binary teacher we show that a first-order phase transition arises in the Bayes-optimal performance.

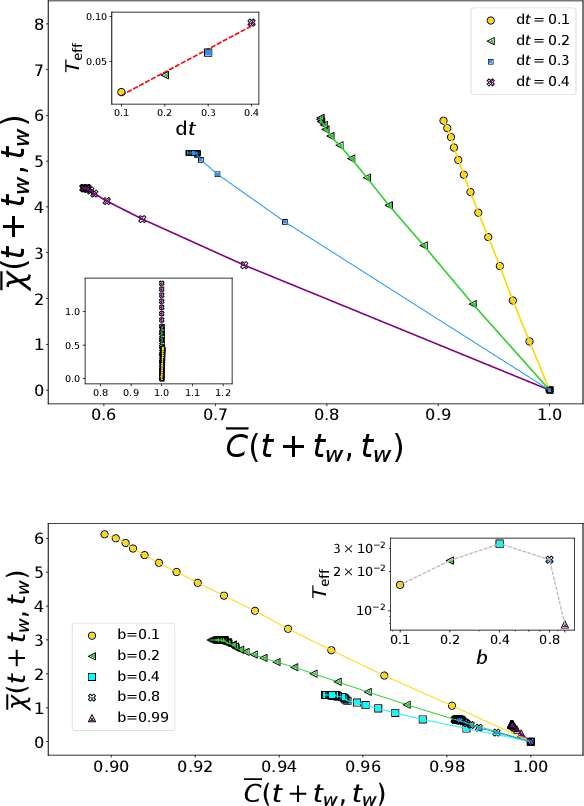
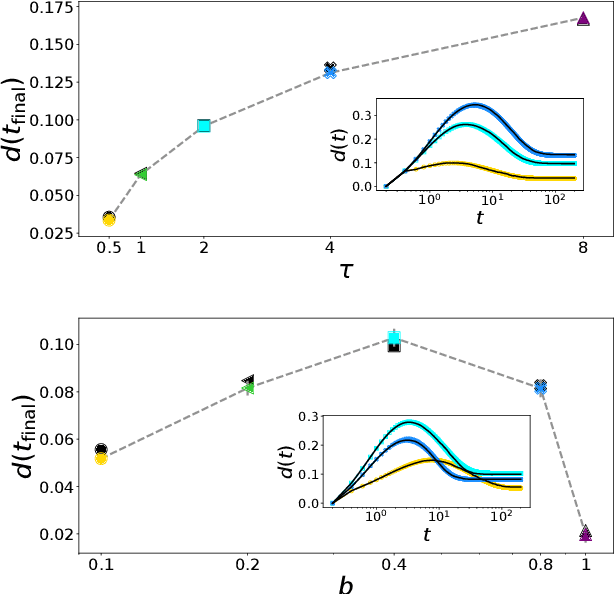
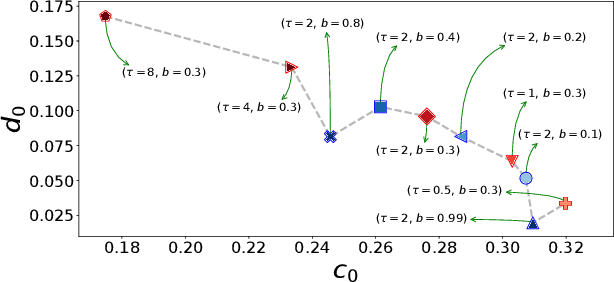
The effective noise of Stochastic Gradient Descent

Stochastic Gradient Descent (SGD) is the workhorse algorithm of deep learning technology. At each step of the training phase, a mini batch of samples is drawn from the training dataset and the weights of the neural network are adjusted according to the performance on this specific subset of examples. The mini-batch sampling procedure introduces a stochastic dynamics to the gradient descent, with a non-trivial state-dependent noise. We characterize the stochasticity of SGD and a recently-introduced variant, persistent SGD, in a prototypical neural network model. In the under-parametrized regime, where the final training error is positive, the SGD dynamics reaches a stationary state and we define an effective temperature from the fluctuation-dissipation theorem, computed from dynamical mean-field theory. We use the effective temperature to quantify the magnitude of the SGD noise as a function of the problem parameters. In the over-parametrized regime, where the training error vanishes, we measure the noise magnitude of SGD by computing the average distance between two replicas of the system with the same initialization and two different realizations of SGD noise. We find that the two noise measures behave similarly as a function of the problem parameters. Moreover, we observe that noisier algorithms lead to wider decision boundaries of the corresponding constraint satisfaction problem.

Stochasticity helps to navigate rough landscapes: comparing gradient-descent-based algorithms in the phase retrieval problem

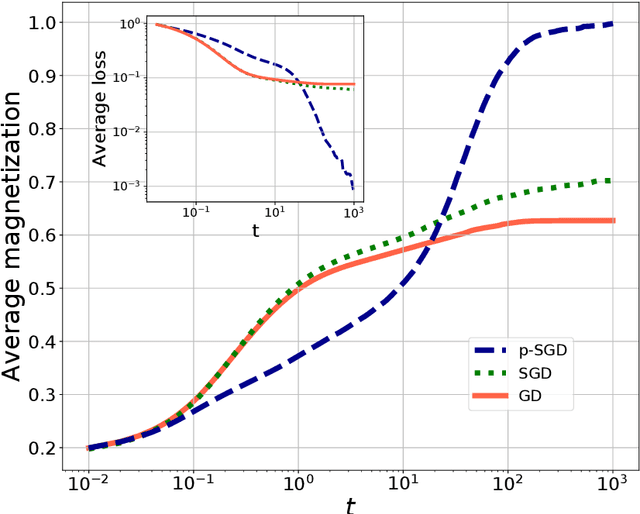
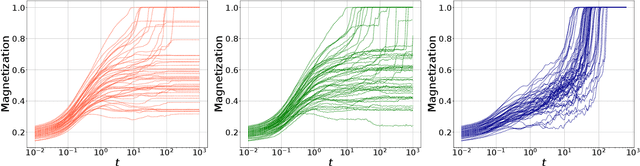
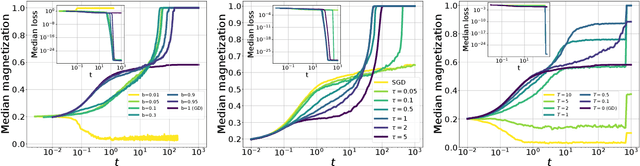
In this paper we investigate how gradient-based algorithms such as gradient descent, (multi-pass) stochastic gradient descent, its persistent variant, and the Langevin algorithm navigate non-convex losslandscapes and which of them is able to reach the best generalization error at limited sample complexity. We consider the loss landscape of the high-dimensional phase retrieval problem as a prototypical highly non-convex example. We observe that for phase retrieval the stochastic variants of gradient descent are able to reach perfect generalization for regions of control parameters where the gradient descent algorithm is not. We apply dynamical mean-field theory from statistical physics to characterize analytically the full trajectories of these algorithms in their continuous-time limit, with a warm start, and for large system sizes. We further unveil several intriguing properties of the landscape and the algorithms such as that the gradient descent can obtain better generalization properties from less informed initializations.

Dynamical mean-field theory for stochastic gradient descent in Gaussian mixture classification

We analyze in a closed form the learning dynamics of stochastic gradient descent (SGD) for a single layer neural network classifying a high-dimensional Gaussian mixture where each cluster is assigned one of two labels. This problem provides a prototype of a non-convex loss landscape with interpolating regimes and a large generalization gap. We define a particular stochastic process for which SGD can be extended to a continuous-time limit that we call stochastic gradient flow. In the full-batch limit we recover the standard gradient flow. We apply dynamical mean-field theory from statistical physics to track the dynamics of the algorithm in the high-dimensional limit via a self-consistent stochastic process. We explore the performance of the algorithm as a function of control parameters shedding light on how it navigates the loss landscape.

The role of regularization in classification of high-dimensional noisy Gaussian mixture

We consider a high-dimensional mixture of two Gaussians in the noisy regime where even an oracle knowing the centers of the clusters misclassifies a small but finite fraction of the points. We provide a rigorous analysis of the generalization error of regularized convex classifiers, including ridge, hinge and logistic regression, in the high-dimensional limit where the number $n$ of samples and their dimension $d$ go to infinity while their ratio is fixed to $\alpha= n/d$. We discuss surprising effects of the regularization that in some cases allows to reach the Bayes-optimal performances. We also illustrate the interpolation peak at low regularization, and analyze the role of the respective sizes of the two clusters.