Learning High-Degree Parities: The Crucial Role of the Initialization

Parities have become a standard benchmark for evaluating learning algorithms. Recent works show that regular neural networks trained by gradient descent can efficiently learn degree $k$ parities on uniform inputs for constant $k$, but fail to do so when $k$ and $d-k$ grow with $d$ (here $d$ is the ambient dimension). However, the case where $k=d-O_d(1)$ (almost-full parities), including the degree $d$ parity (the full parity), has remained unsettled. This paper shows that for gradient descent on regular neural networks, learnability depends on the initial weight distribution. On one hand, the discrete Rademacher initialization enables efficient learning of almost-full parities, while on the other hand, its Gaussian perturbation with large enough constant standard deviation $\sigma$ prevents it. The positive result for almost-full parities is shown to hold up to $\sigma=O(d^{-1})$, pointing to questions about a sharper threshold phenomenon. Unlike statistical query (SQ) learning, where a singleton function class like the full parity is trivially learnable, our negative result applies to a fixed function and relies on an initial gradient alignment measure of potential broader relevance to neural networks learning.

Provable Advantage of Curriculum Learning on Parity Targets with Mixed Inputs

Experimental results have shown that curriculum learning, i.e., presenting simpler examples before more complex ones, can improve the efficiency of learning. Some recent theoretical results also showed that changing the sampling distribution can help neural networks learn parities, with formal results only for large learning rates and one-step arguments. Here we show a separation result in the number of training steps with standard (bounded) learning rates on a common sample distribution: if the data distribution is a mixture of sparse and dense inputs, there exists a regime in which a 2-layer ReLU neural network trained by a curriculum noisy-GD (or SGD) algorithm that uses sparse examples first, can learn parities of sufficiently large degree, while any fully connected neural network of possibly larger width or depth trained by noisy-GD on the unordered samples cannot learn without additional steps. We also provide experimental results supporting the qualitative separation beyond the specific regime of the theoretical results.

A Mathematical Model for Curriculum Learning

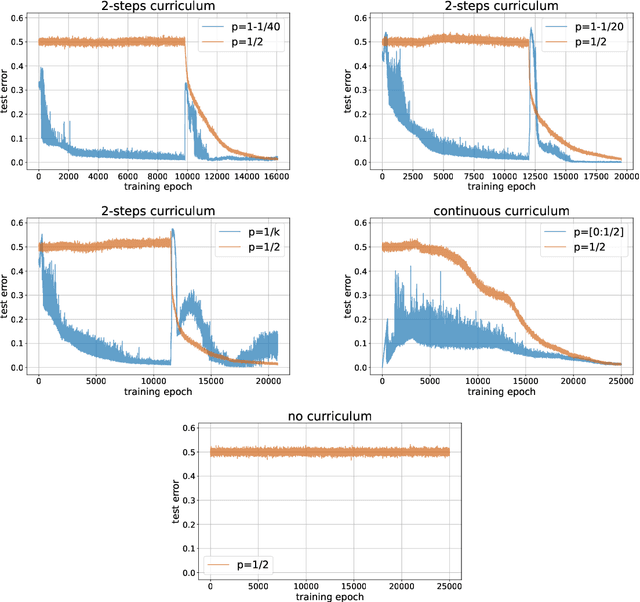
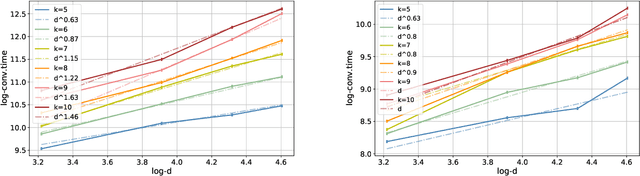
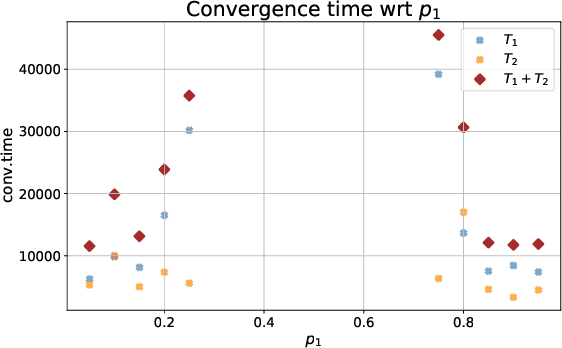
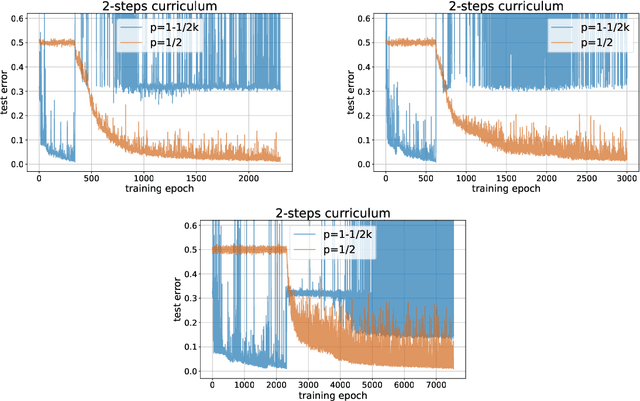
Curriculum learning (CL) - training using samples that are generated and presented in a meaningful order - was introduced in the machine learning context around a decade ago. While CL has been extensively used and analysed empirically, there has been very little mathematical justification for its advantages. We introduce a CL model for learning the class of k-parities on d bits of a binary string with a neural network trained by stochastic gradient descent (SGD). We show that a wise choice of training examples, involving two or more product distributions, allows to reduce significantly the computational cost of learning this class of functions, compared to learning under the uniform distribution. We conduct experiments to support our analysis. Furthermore, we show that for another class of functions - namely the `Hamming mixtures' - CL strategies involving a bounded number of product distributions are not beneficial, while we conjecture that CL with unbounded many curriculum steps can learn this class efficiently.

Learning to Reason with Neural Networks: Generalization, Unseen Data and Boolean Measures

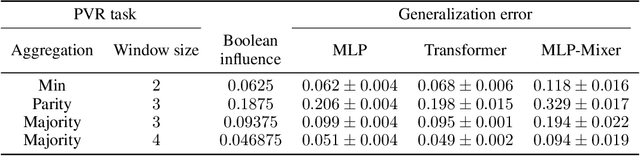
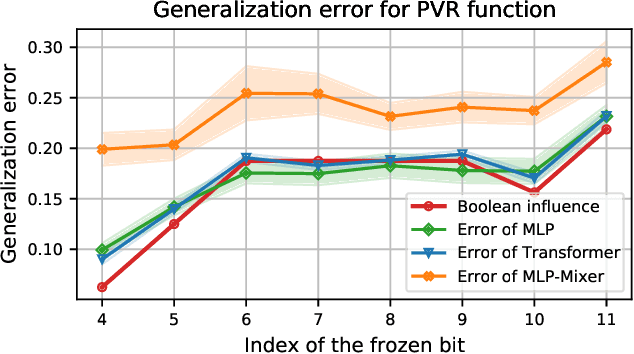
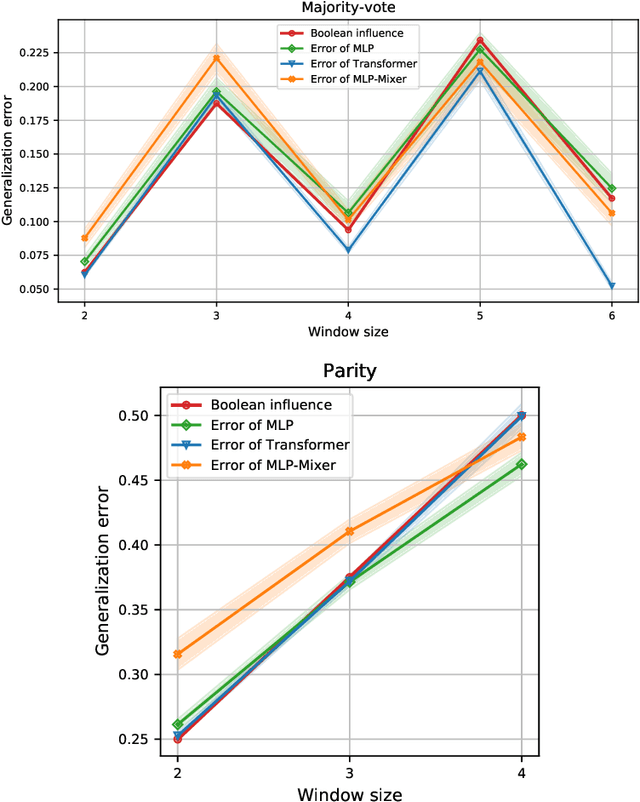
This paper considers the Pointer Value Retrieval (PVR) benchmark introduced in [ZRKB21], where a 'reasoning' function acts on a string of digits to produce the label. More generally, the paper considers the learning of logical functions with gradient descent (GD) on neural networks. It is first shown that in order to learn logical functions with gradient descent on symmetric neural networks, the generalization error can be lower-bounded in terms of the noise-stability of the target function, supporting a conjecture made in [ZRKB21]. It is then shown that in the distribution shift setting, when the data withholding corresponds to freezing a single feature (referred to as canonical holdout), the generalization error of gradient descent admits a tight characterization in terms of the Boolean influence for several relevant architectures. This is shown on linear models and supported experimentally on other models such as MLPs and Transformers. In particular, this puts forward the hypothesis that for such architectures and for learning logical functions such as PVR functions, GD tends to have an implicit bias towards low-degree representations, which in turn gives the Boolean influence for the generalization error under quadratic loss.

Learning curves for the multi-class teacher-student perceptron

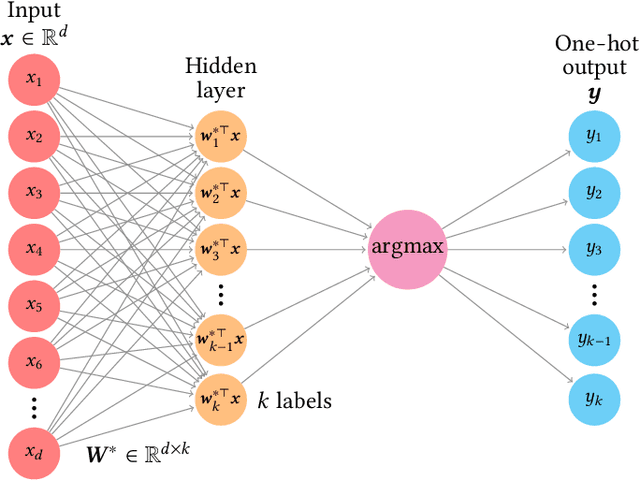
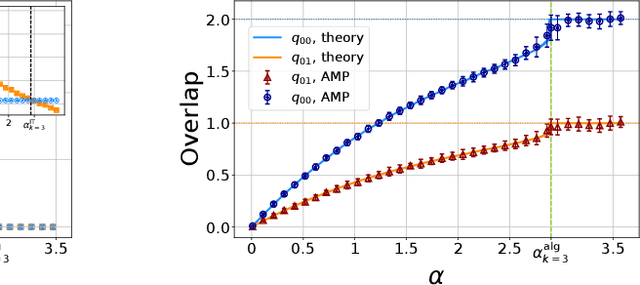
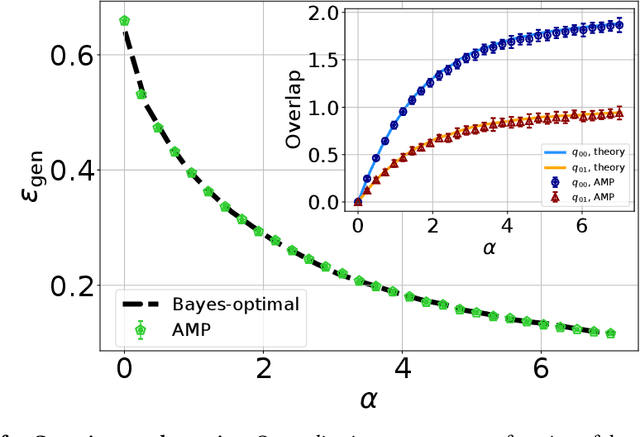
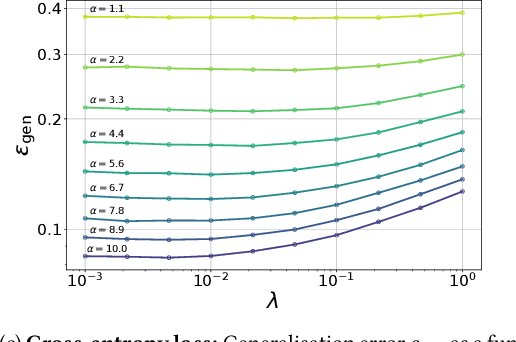
One of the most classical results in high-dimensional learning theory provides a closed-form expression for the generalisation error of binary classification with the single-layer teacher-student perceptron on i.i.d. Gaussian inputs. Both Bayes-optimal estimation and empirical risk minimisation (ERM) were extensively analysed for this setting. At the same time, a considerable part of modern machine learning practice concerns multi-class classification. Yet, an analogous analysis for the corresponding multi-class teacher-student perceptron was missing. In this manuscript we fill this gap by deriving and evaluating asymptotic expressions for both the Bayes-optimal and ERM generalisation errors in the high-dimensional regime. For Gaussian teacher weights, we investigate the performance of ERM with both cross-entropy and square losses, and explore the role of ridge regularisation in approaching Bayes-optimality. In particular, we observe that regularised cross-entropy minimisation yields close-to-optimal accuracy. Instead, for a binary teacher we show that a first-order phase transition arises in the Bayes-optimal performance.

An initial alignment between neural network and target is needed for gradient descent to learn

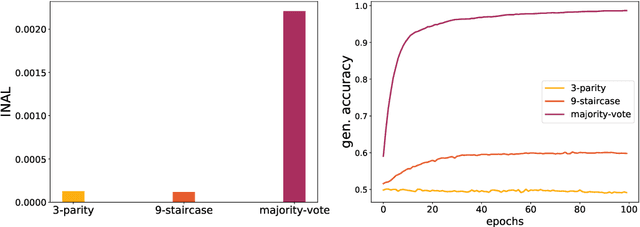
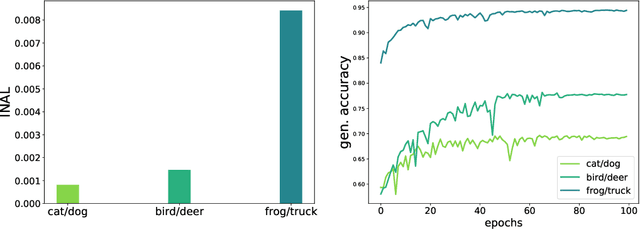
This paper introduces the notion of "Initial Alignment" (INAL) between a neural network at initialization and a target function. It is proved that if a network and target function do not have a noticeable INAL, then noisy gradient descent on a fully connected network with normalized i.i.d. initialization will not learn in polynomial time. Thus a certain amount of knowledge about the target (measured by the INAL) is needed in the architecture design. This also provides an answer to an open problem posed in [AS20]. The results are based on deriving lower-bounds for descent algorithms on symmetric neural networks without explicit knowledge of the target function beyond its INAL.

Regularization by Misclassification in ReLU Neural Networks

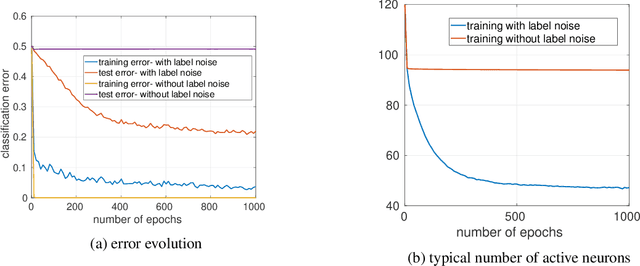
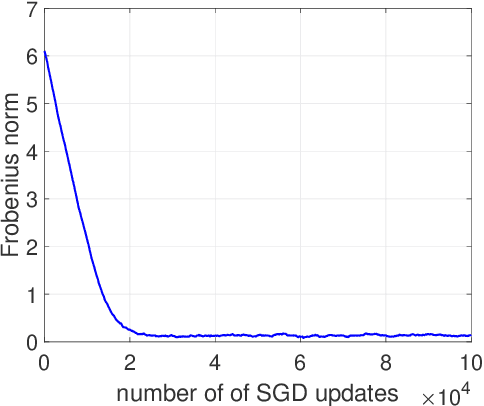
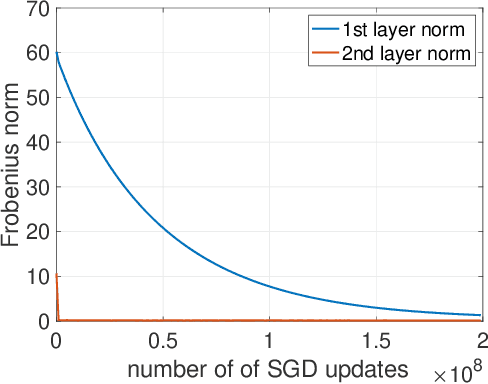
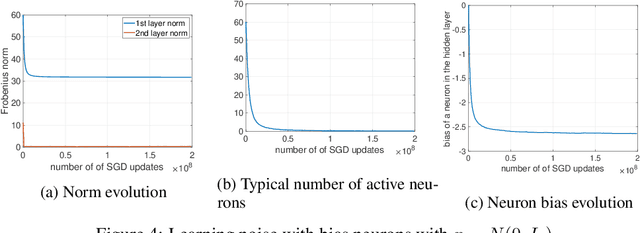
We study the implicit bias of ReLU neural networks trained by a variant of SGD where at each step, the label is changed with probability $p$ to a random label (label smoothing being a close variant of this procedure). Our experiments demonstrate that label noise propels the network to a sparse solution in the following sense: for a typical input, a small fraction of neurons are active, and the firing pattern of the hidden layers is sparser. In fact, for some instances, an appropriate amount of label noise does not only sparsify the network but further reduces the test error. We then turn to the theoretical analysis of such sparsification mechanisms, focusing on the extremal case of $p=1$. We show that in this case, the network withers as anticipated from experiments, but surprisingly, in different ways that depend on the learning rate and the presence of bias, with either weights vanishing or neurons ceasing to fire.