A Mathematical Model for Curriculum Learning

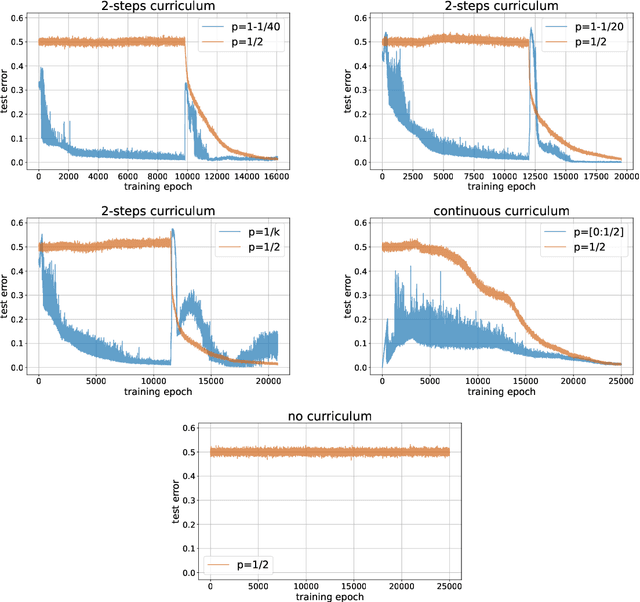
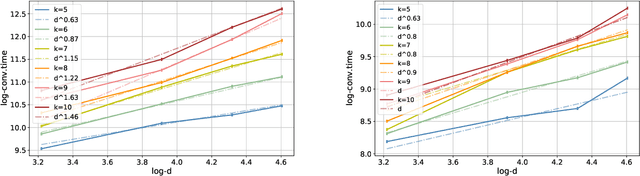
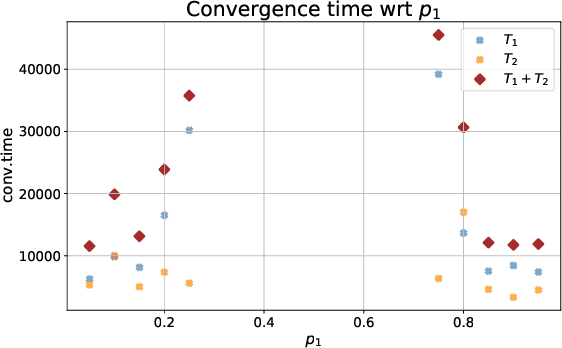
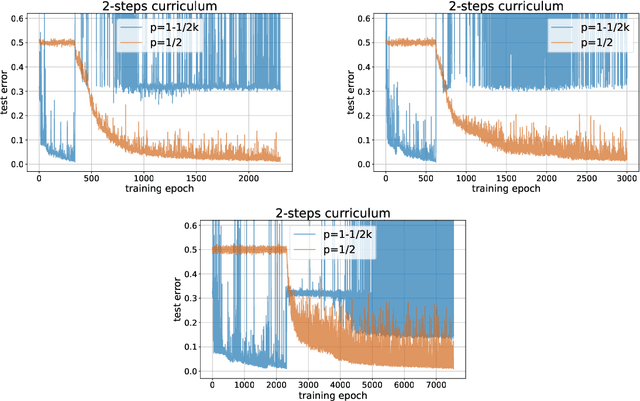
Curriculum learning (CL) - training using samples that are generated and presented in a meaningful order - was introduced in the machine learning context around a decade ago. While CL has been extensively used and analysed empirically, there has been very little mathematical justification for its advantages. We introduce a CL model for learning the class of k-parities on d bits of a binary string with a neural network trained by stochastic gradient descent (SGD). We show that a wise choice of training examples, involving two or more product distributions, allows to reduce significantly the computational cost of learning this class of functions, compared to learning under the uniform distribution. We conduct experiments to support our analysis. Furthermore, we show that for another class of functions - namely the `Hamming mixtures' - CL strategies involving a bounded number of product distributions are not beneficial, while we conjecture that CL with unbounded many curriculum steps can learn this class efficiently.