Low-dimensional Functions are Efficiently Learnable under Randomly Biased Distributions

The problem of learning single index and multi index models has gained significant interest as a fundamental task in high-dimensional statistics. Many recent works have analysed gradient-based methods, particularly in the setting of isotropic data distributions, often in the context of neural network training. Such studies have uncovered precise characterisations of algorithmic sample complexity in terms of certain analytic properties of the target function, such as the leap, information, and generative exponents. These properties establish a quantitative separation between low and high complexity learning tasks. In this work, we show that high complexity cases are rare. Specifically, we prove that introducing a small random perturbation to the data distribution--via a random shift in the first moment--renders any Gaussian single index model as easy to learn as a linear function. We further extend this result to a class of multi index models, namely sparse Boolean functions, also known as Juntas.

Noise Sensitivity of Hierarchical Functions and Deep Learning Lower Bounds in General Product Measures

Recent works explore deep learning's success by examining functions or data with hierarchical structure. Complementarily, research on gradient descent performance for deep nets has shown that noise sensitivity of functions under independent and identically distributed (i.i.d.) Bernoulli inputs establishes learning complexity bounds. This paper aims to bridge these research streams by demonstrating that functions constructed through repeated composition of non-linear functions are noise sensitive under general product measures.

Efficiently Learning Markov Random Fields from Dynamics

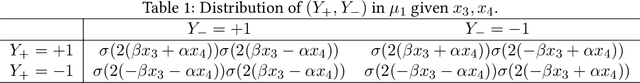
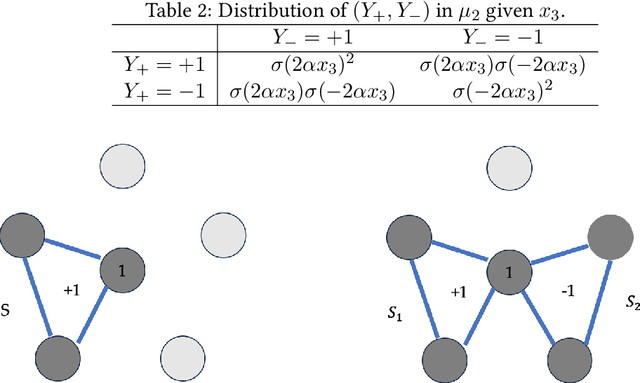
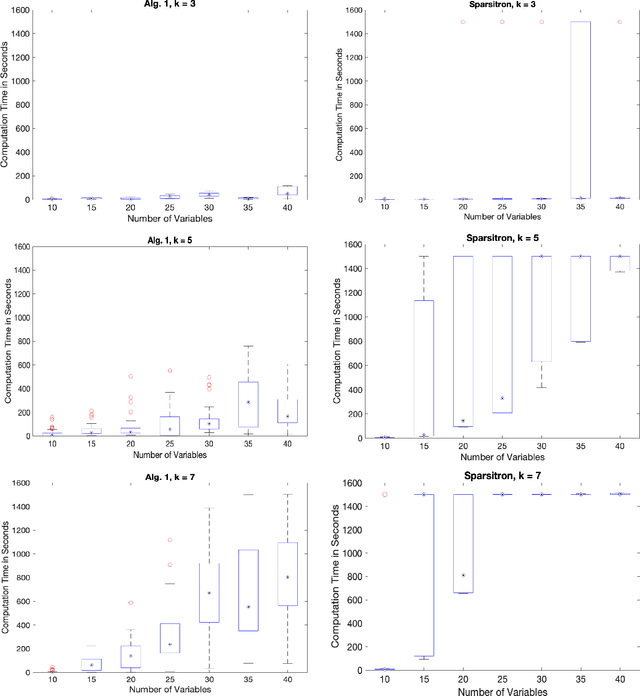
An important task in high-dimensional statistics is learning the parameters or dependency structure of an undirected graphical model, or Markov random field (MRF). Much of the prior work on this problem assumes access to i.i.d. samples from the MRF distribution and state-of-the-art algorithms succeed using $n^{\Theta(k)}$ runtime, where $n$ is the dimension and $k$ is the order of the interactions. However, well-known reductions from the sparse parity with noise problem imply that given i.i.d. samples from a sparse, order-$k$ MRF, any learning algorithm likely requires $n^{\Omega(k)}$ time, impeding the potential for significant computational improvements. In this work, we demonstrate that these fundamental barriers for learning MRFs can surprisingly be completely circumvented when learning from natural, dynamical samples. We show that in bounded-degree MRFs, the dependency structure and parameters can be recovered using a trajectory of Glauber dynamics of length $O(n \log n)$ with runtime $O(n^2 \log n)$. The implicit constants depend only on the degree and non-degeneracy parameters of the model, but not the dimension $n$. In particular, learning MRFs from dynamics is $\textit{provably computationally easier}$ than learning from i.i.d. samples under standard hardness assumptions.

Sample-Efficient Linear Regression with Self-Selection Bias

We consider the problem of linear regression with self-selection bias in the unknown-index setting, as introduced in recent work by Cherapanamjeri, Daskalakis, Ilyas, and Zampetakis [STOC 2023]. In this model, one observes $m$ i.i.d. samples $(\mathbf{x}_{\ell},z_{\ell})_{\ell=1}^m$ where $z_{\ell}=\max_{i\in [k]}\{\mathbf{x}_{\ell}^T\mathbf{w}_i+\eta_{i,\ell}\}$, but the maximizing index $i_{\ell}$ is unobserved. Here, the $\mathbf{x}_{\ell}$ are assumed to be $\mathcal{N}(0,I_n)$ and the noise distribution $\mathbf{\eta}_{\ell}\sim \mathcal{D}$ is centered and independent of $\mathbf{x}_{\ell}$. We provide a novel and near optimally sample-efficient (in terms of $k$) algorithm to recover $\mathbf{w}_1,\ldots,\mathbf{w}_k\in \mathbb{R}^n$ up to additive $\ell_2$-error $\varepsilon$ with polynomial sample complexity $\tilde{O}(n)\cdot \mathsf{poly}(k,1/\varepsilon)$ and significantly improved time complexity $\mathsf{poly}(n,k,1/\varepsilon)+O(\log(k)/\varepsilon)^{O(k)}$. When $k=O(1)$, our algorithm runs in $\mathsf{poly}(n,1/\varepsilon)$ time, generalizing the polynomial guarantee of an explicit moment matching algorithm of Cherapanamjeri, et al. for $k=2$ and when it is known that $\mathcal{D}=\mathcal{N}(0,I_k)$. Our algorithm succeeds under significantly relaxed noise assumptions, and therefore also succeeds in the related setting of max-linear regression where the added noise is taken outside the maximum. For this problem, our algorithm is efficient in a much larger range of $k$ than the state-of-the-art due to Ghosh, Pananjady, Guntuboyina, and Ramchandran [IEEE Trans. Inf. Theory 2022] for not too small $\varepsilon$, and leads to improved algorithms for any $\varepsilon$ by providing a warm start for existing local convergence methods.

Reconstructing the Geometry of Random Geometric Graphs

Random geometric graphs are random graph models defined on metric spaces. Such a model is defined by first sampling points from a metric space and then connecting each pair of sampled points with probability that depends on their distance, independently among pairs. In this work, we show how to efficiently reconstruct the geometry of the underlying space from the sampled graph under the manifold assumption, i.e., assuming that the underlying space is a low dimensional manifold and that the connection probability is a strictly decreasing function of the Euclidean distance between the points in a given embedding of the manifold in $\mathbb{R}^N$. Our work complements a large body of work on manifold learning, where the goal is to recover a manifold from sampled points sampled in the manifold along with their (approximate) distances.

A Unified Approach to Learning Ising Models: Beyond Independence and Bounded Width

We revisit the problem of efficiently learning the underlying parameters of Ising models from data. Current algorithmic approaches achieve essentially optimal sample complexity when given i.i.d. samples from the stationary measure and the underlying model satisfies "width" bounds on the total $\ell_1$ interaction involving each node. We show that a simple existing approach based on node-wise logistic regression provably succeeds at recovering the underlying model in several new settings where these assumptions are violated: (1) Given dynamically generated data from a wide variety of local Markov chains, like block or round-robin dynamics, logistic regression recovers the parameters with optimal sample complexity up to $\log\log n$ factors. This generalizes the specialized algorithm of Bresler, Gamarnik, and Shah [IEEE Trans. Inf. Theory'18] for structure recovery in bounded degree graphs from Glauber dynamics. (2) For the Sherrington-Kirkpatrick model of spin glasses, given $\mathsf{poly}(n)$ independent samples, logistic regression recovers the parameters in most of the known high-temperature regime via a simple reduction to weaker structural properties of the measure. This improves on recent work of Anari, Jain, Koehler, Pham, and Vuong [ArXiv'23] which gives distribution learning at higher temperature. (3) As a simple byproduct of our techniques, logistic regression achieves an exponential improvement in learning from samples in the M-regime of data considered by Dutt, Lokhov, Vuffray, and Misra [ICML'21] as well as novel guarantees for learning from the adversarial Glauber dynamics of Chin, Moitra, Mossel, and Sandon [ArXiv'23]. Our approach thus significantly generalizes the elegant analysis of Wu, Sanghavi, and Dimakis [Neurips'19] without any algorithmic modification.

Combinative Cumulative Knowledge Processes

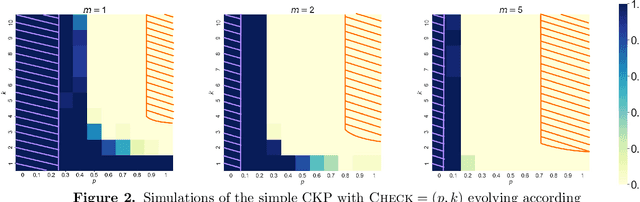
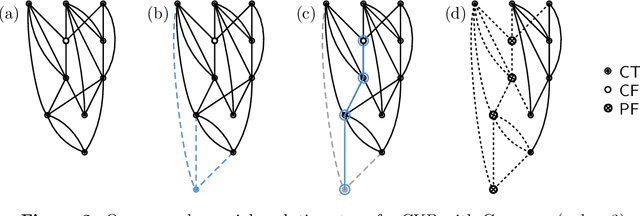
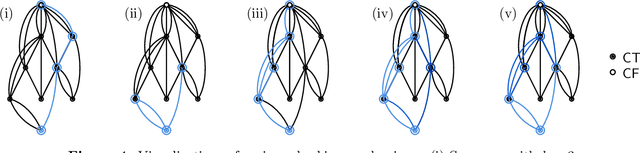
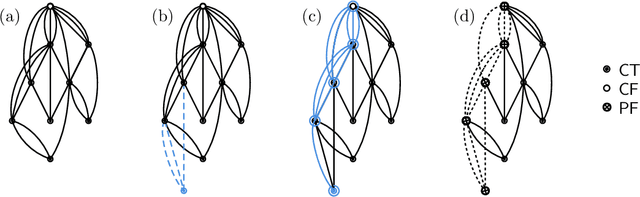
We analyze Cumulative Knowledge Processes, introduced by Ben-Eliezer, Mikulincer, Mossel, and Sudan (ITCS 2023), in the setting of "directed acyclic graphs", i.e., when new units of knowledge may be derived by combining multiple previous units of knowledge. The main considerations in this model are the role of errors (when new units may be erroneous) and local checking (where a few antecedent units of knowledge are checked when a new unit of knowledge is discovered). The aforementioned work defined this model but only analyzed an idealized and simplified "tree-like" setting, i.e., a setting where new units of knowledge only depended directly on one previously generated unit of knowledge. The main goal of our work is to understand when the general process is safe, i.e., when the effect of errors remains under control. We provide some necessary and some sufficient conditions for safety. As in the earlier work, we demonstrate that the frequency of checking as well as the depth of the checks play a crucial role in determining safety. A key new parameter in the current work is the $\textit{combination factor}$ which is the distribution of the number of units $M$ of old knowledge that a new unit of knowledge depends on. Our results indicate that a large combination factor can compensate for a small depth of checking. The dependency of the safety on the combination factor is far from trivial. Indeed some of our main results are stated in terms of $\mathbb{E}\{1/M\}$ while others depend on $\mathbb{E}\{M\}$.

A Mathematical Model for Curriculum Learning

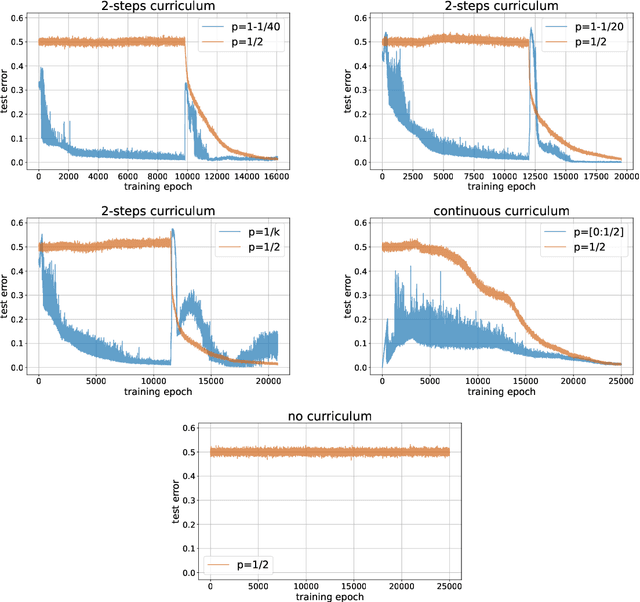
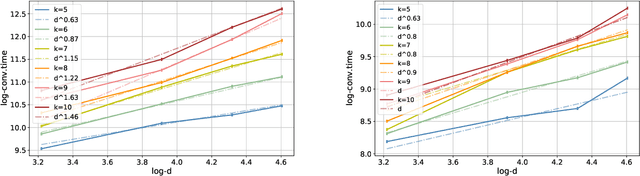
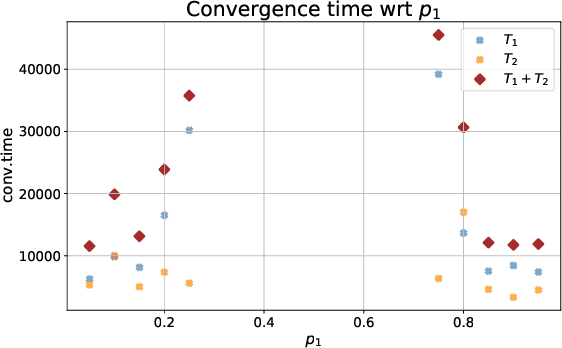
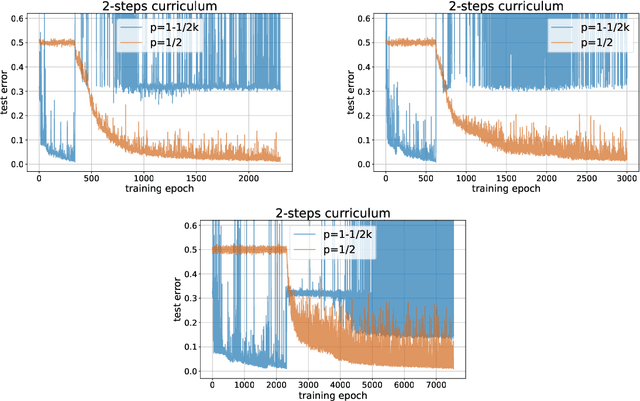
Curriculum learning (CL) - training using samples that are generated and presented in a meaningful order - was introduced in the machine learning context around a decade ago. While CL has been extensively used and analysed empirically, there has been very little mathematical justification for its advantages. We introduce a CL model for learning the class of k-parities on d bits of a binary string with a neural network trained by stochastic gradient descent (SGD). We show that a wise choice of training examples, involving two or more product distributions, allows to reduce significantly the computational cost of learning this class of functions, compared to learning under the uniform distribution. We conduct experiments to support our analysis. Furthermore, we show that for another class of functions - namely the `Hamming mixtures' - CL strategies involving a bounded number of product distributions are not beneficial, while we conjecture that CL with unbounded many curriculum steps can learn this class efficiently.

Efficient Reconstruction of Stochastic Pedigrees: Some Steps From Theory to Practice

In an extant population, how much information do extant individuals provide on the pedigree of their ancestors? Recent work by Kim, Mossel, Ramnarayan and Turner (2020) studied this question under a number of simplifying assumptions, including random mating, fixed length inheritance blocks and sufficiently large founding population. They showed that under these conditions if the average number of offspring is a sufficiently large constant, then it is possible to recover a large fraction of the pedigree structure and genetic content by an algorithm they named REC-GEN. We are interested in studying the performance of REC-GEN on simulated data generated according to the model. As a first step, we improve the running time of the algorithm. However, we observe that even the faster version of the algorithm does not do well in any simulations in recovering the pedigree beyond 2 generations. We claim that this is due to the inbreeding present in any setting where the algorithm can be run, even on simulated data. To support the claim we show that a main step of the algorithm, called ancestral reconstruction, performs accurately in a idealized setting with no inbreeding but performs poorly in random mating populations. To overcome the poor behavior of REC-GEN we introduce a Belief-Propagation based heuristic that accounts for the inbreeding and performs much better in our simulations.

Spectral Algorithms Optimally Recover (Censored) Planted Dense Subgraphs

We study spectral algorithms for the planted dense subgraph problem (PDS), as well as for a censored variant (CPDS) of PDS, where the edge statuses are missing at random. More precisely, in the PDS model, we consider $n$ vertices and a random subset of vertices $S^{\star}$ of size $\Omega(n)$, such that two vertices share an edge with probability $p$ if both of them are in $S^{\star}$, and all other edges are present with probability $q$, independently. The goal is to recover $S^{\star}$ from one observation of the network. In the CPDS model, edge statuses are revealed with probability $\frac{t \log n}{n}$. For the PDS model, we show that a simple spectral algorithm based on the top two eigenvectors of the adjacency matrix can recover $S^{\star}$ up to the information theoretic threshold. Prior work by Hajek, Wu and Xu required a less efficient SDP based algorithm to recover $S^{\star}$ up to the information theoretic threshold. For the CDPS model, we obtain the information theoretic limit for the recovery problem, and further show that a spectral algorithm based on a special matrix called the signed adjacency matrix recovers $S^{\star}$ up to the information theoretic threshold.