Overcomplete Tensor Decomposition via Koszul-Young Flattenings

Motivated by connections between algebraic complexity lower bounds and tensor decompositions, we investigate Koszul-Young flattenings, which are the main ingredient in recent lower bounds for matrix multiplication. Based on this tool we give a new algorithm for decomposing an $n_1 \times n_2 \times n_3$ tensor as the sum of a minimal number of rank-1 terms, and certifying uniqueness of this decomposition. For $n_1 \le n_2 \le n_3$ with $n_1 \to \infty$ and $n_3/n_2 = O(1)$, our algorithm is guaranteed to succeed when the tensor rank is bounded by $r \le (1-\epsilon)(n_2 + n_3)$ for an arbitrary $\epsilon > 0$, provided the tensor components are generically chosen. For any fixed $\epsilon$, the runtime is polynomial in $n_3$. When $n_2 = n_3 = n$, our condition on the rank gives a factor-of-2 improvement over the classical simultaneous diagonalization algorithm, which requires $r \le n$, and also improves on the recent algorithm of Koiran (2024) which requires $r \le 4n/3$. It also improves on the PhD thesis of Persu (2018) which solves rank detection for $r \leq 3n/2$. We complement our upper bounds by showing limitations, in particular that no flattening of the style we consider can surpass rank $n_2 + n_3$. Furthermore, for $n \times n \times n$ tensors, we show that an even more general class of degree-$d$ polynomial flattenings cannot surpass rank $Cn$ for a constant $C = C(d)$. This suggests that for tensor decompositions, the case of generic components may be fundamentally harder than that of random components, where efficient decomposition is possible even in highly overcomplete settings.

Model Stealing for Any Low-Rank Language Model

Model stealing, where a learner tries to recover an unknown model via carefully chosen queries, is a critical problem in machine learning, as it threatens the security of proprietary models and the privacy of data they are trained on. In recent years, there has been particular interest in stealing large language models (LLMs). In this paper, we aim to build a theoretical understanding of stealing language models by studying a simple and mathematically tractable setting. We study model stealing for Hidden Markov Models (HMMs), and more generally low-rank language models. We assume that the learner works in the conditional query model, introduced by Kakade, Krishnamurthy, Mahajan and Zhang. Our main result is an efficient algorithm in the conditional query model, for learning any low-rank distribution. In other words, our algorithm succeeds at stealing any language model whose output distribution is low-rank. This improves upon the previous result by Kakade, Krishnamurthy, Mahajan and Zhang, which also requires the unknown distribution to have high "fidelity", a property that holds only in restricted cases. There are two key insights behind our algorithm: First, we represent the conditional distributions at each timestep by constructing barycentric spanners among a collection of vectors of exponentially large dimension. Second, for sampling from our representation, we iteratively solve a sequence of convex optimization problems that involve projection in relative entropy to prevent compounding of errors over the length of the sequence. This is an interesting example where, at least theoretically, allowing a machine learning model to solve more complex problems at inference time can lead to drastic improvements in its performance.

Towards characterizing the value of edge embeddings in Graph Neural Networks

Graph neural networks (GNNs) are the dominant approach to solving machine learning problems defined over graphs. Despite much theoretical and empirical work in recent years, our understanding of finer-grained aspects of architectural design for GNNs remains impoverished. In this paper, we consider the benefits of architectures that maintain and update edge embeddings. On the theoretical front, under a suitable computational abstraction for a layer in the model, as well as memory constraints on the embeddings, we show that there are natural tasks on graphical models for which architectures leveraging edge embeddings can be much shallower. Our techniques are inspired by results on time-space tradeoffs in theoretical computer science. Empirically, we show architectures that maintain edge embeddings almost always improve on their node-based counterparts -- frequently significantly so in topologies that have ``hub'' nodes.

Efficiently Learning Markov Random Fields from Dynamics

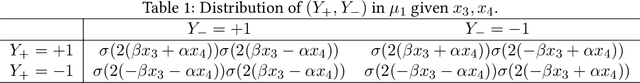
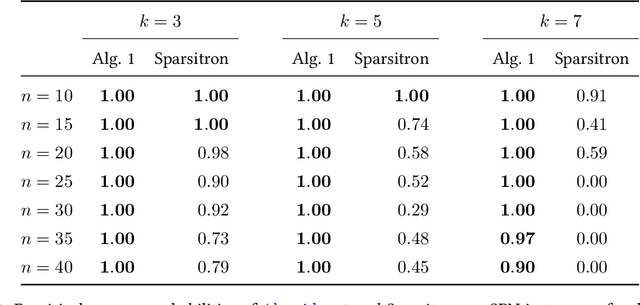
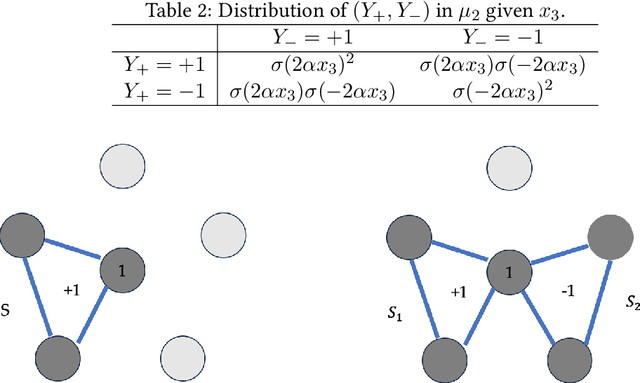
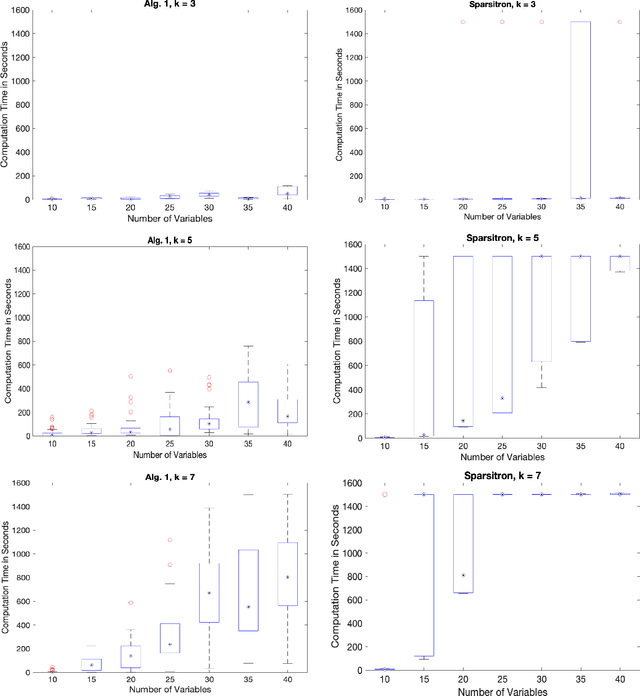
An important task in high-dimensional statistics is learning the parameters or dependency structure of an undirected graphical model, or Markov random field (MRF). Much of the prior work on this problem assumes access to i.i.d. samples from the MRF distribution and state-of-the-art algorithms succeed using $n^{\Theta(k)}$ runtime, where $n$ is the dimension and $k$ is the order of the interactions. However, well-known reductions from the sparse parity with noise problem imply that given i.i.d. samples from a sparse, order-$k$ MRF, any learning algorithm likely requires $n^{\Omega(k)}$ time, impeding the potential for significant computational improvements. In this work, we demonstrate that these fundamental barriers for learning MRFs can surprisingly be completely circumvented when learning from natural, dynamical samples. We show that in bounded-degree MRFs, the dependency structure and parameters can be recovered using a trajectory of Glauber dynamics of length $O(n \log n)$ with runtime $O(n^2 \log n)$. The implicit constants depend only on the degree and non-degeneracy parameters of the model, but not the dimension $n$. In particular, learning MRFs from dynamics is $\textit{provably computationally easier}$ than learning from i.i.d. samples under standard hardness assumptions.

The Role of Inherent Bellman Error in Offline Reinforcement Learning with Linear Function Approximation

In this paper, we study the offline RL problem with linear function approximation. Our main structural assumption is that the MDP has low inherent Bellman error, which stipulates that linear value functions have linear Bellman backups with respect to the greedy policy. This assumption is natural in that it is essentially the minimal assumption required for value iteration to succeed. We give a computationally efficient algorithm which succeeds under a single-policy coverage condition on the dataset, namely which outputs a policy whose value is at least that of any policy which is well-covered by the dataset. Even in the setting when the inherent Bellman error is 0 (termed linear Bellman completeness), our algorithm yields the first known guarantee under single-policy coverage. In the setting of positive inherent Bellman error ${\varepsilon_{\mathrm{BE}}} > 0$, we show that the suboptimality error of our algorithm scales with $\sqrt{\varepsilon_{\mathrm{BE}}}$. Furthermore, we prove that the scaling of the suboptimality with $\sqrt{\varepsilon_{\mathrm{BE}}}$ cannot be improved for any algorithm. Our lower bound stands in contrast to many other settings in reinforcement learning with misspecification, where one can typically obtain performance that degrades linearly with the misspecification error.

Linear Bellman Completeness Suffices for Efficient Online Reinforcement Learning with Few Actions

One of the most natural approaches to reinforcement learning (RL) with function approximation is value iteration, which inductively generates approximations to the optimal value function by solving a sequence of regression problems. To ensure the success of value iteration, it is typically assumed that Bellman completeness holds, which ensures that these regression problems are well-specified. We study the problem of learning an optimal policy under Bellman completeness in the online model of RL with linear function approximation. In the linear setting, while statistically efficient algorithms are known under Bellman completeness (e.g., Jiang et al. (2017); Zanette et al. (2020)), these algorithms all rely on the principle of global optimism which requires solving a nonconvex optimization problem. In particular, it has remained open as to whether computationally efficient algorithms exist. In this paper we give the first polynomial-time algorithm for RL under linear Bellman completeness when the number of actions is any constant.

Edit Distance Robust Watermarks for Language Models

Motivated by the problem of detecting AI-generated text, we consider the problem of watermarking the output of language models with provable guarantees. We aim for watermarks which satisfy: (a) undetectability, a cryptographic notion introduced by Christ, Gunn & Zamir (2024) which stipulates that it is computationally hard to distinguish watermarked language model outputs from the model's actual output distribution; and (b) robustness to channels which introduce a constant fraction of adversarial insertions, substitutions, and deletions to the watermarked text. Earlier schemes could only handle stochastic substitutions and deletions, and thus we are aiming for a more natural and appealing robustness guarantee that holds with respect to edit distance. Our main result is a watermarking scheme which achieves both undetectability and robustness to edits when the alphabet size for the language model is allowed to grow as a polynomial in the security parameter. To derive such a scheme, we follow an approach introduced by Christ & Gunn (2024), which proceeds via first constructing pseudorandom codes satisfying undetectability and robustness properties analogous to those above; our key idea is to handle adversarial insertions and deletions by interpreting the symbols as indices into the codeword, which we call indexing pseudorandom codes. Additionally, our codes rely on weaker computational assumptions than used in previous work. Then we show that there is a generic transformation from such codes over large alphabets to watermarking schemes for arbitrary language models.

Structure learning of Hamiltonians from real-time evolution

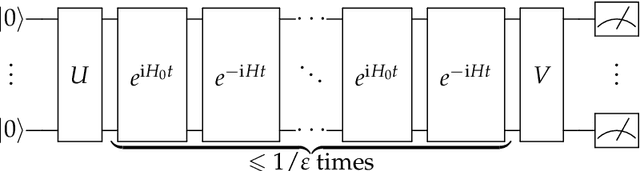
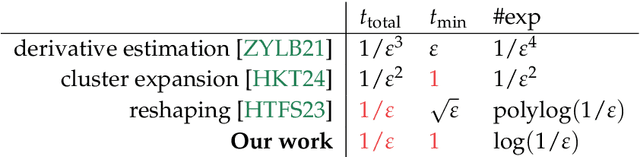
We initiate the study of Hamiltonian structure learning from real-time evolution: given the ability to apply $e^{-\mathrm{i} Ht}$ for an unknown local Hamiltonian $H = \sum_{a = 1}^m \lambda_a E_a$ on $n$ qubits, the goal is to recover $H$. This problem is already well-studied under the assumption that the interaction terms, $E_a$, are given, and only the interaction strengths, $\lambda_a$, are unknown. But is it possible to learn a local Hamiltonian without prior knowledge of its interaction structure? We present a new, general approach to Hamiltonian learning that not only solves the challenging structure learning variant, but also resolves other open questions in the area, all while achieving the gold standard of Heisenberg-limited scaling. In particular, our algorithm recovers the Hamiltonian to $\varepsilon$ error with an evolution time scaling with $1/\varepsilon$, and has the following appealing properties: (1) it does not need to know the Hamiltonian terms; (2) it works beyond the short-range setting, extending to any Hamiltonian $H$ where the sum of terms interacting with a qubit has bounded norm; (3) it evolves according to $H$ in constant time $t$ increments, thus achieving constant time resolution. To our knowledge, no prior algorithm with Heisenberg-limited scaling existed with even one of these properties. As an application, we can also learn Hamiltonians exhibiting power-law decay up to accuracy $\varepsilon$ with total evolution time beating the standard limit of $1/\varepsilon^2$.

Exploration is Harder than Prediction: Cryptographically Separating Reinforcement Learning from Supervised Learning

Supervised learning is often computationally easy in practice. But to what extent does this mean that other modes of learning, such as reinforcement learning (RL), ought to be computationally easy by extension? In this work we show the first cryptographic separation between RL and supervised learning, by exhibiting a class of block MDPs and associated decoding functions where reward-free exploration is provably computationally harder than the associated regression problem. We also show that there is no computationally efficient algorithm for reward-directed RL in block MDPs, even when given access to an oracle for this regression problem. It is known that being able to perform regression in block MDPs is necessary for finding a good policy; our results suggest that it is not sufficient. Our separation lower bound uses a new robustness property of the Learning Parities with Noise (LPN) hardness assumption, which is crucial in handling the dependent nature of RL data. We argue that separations and oracle lower bounds, such as ours, are a more meaningful way to prove hardness of learning because the constructions better reflect the practical reality that supervised learning by itself is often not the computational bottleneck.

Precise Error Rates for Computationally Efficient Testing

We revisit the fundamental question of simple-versus-simple hypothesis testing with an eye towards computational complexity, as the statistically optimal likelihood ratio test is often computationally intractable in high-dimensional settings. In the classical spiked Wigner model (with a general i.i.d. spike prior) we show that an existing test based on linear spectral statistics achieves the best possible tradeoff curve between type I and type II error rates among all computationally efficient tests, even though there are exponential-time tests that do better. This result is conditional on an appropriate complexity-theoretic conjecture, namely a natural strengthening of the well-established low-degree conjecture. Our result shows that the spectrum is a sufficient statistic for computationally bounded tests (but not for all tests). To our knowledge, our approach gives the first tool for reasoning about the precise asymptotic testing error achievable with efficient computation. The main ingredients required for our hardness result are a sharp bound on the norm of the low-degree likelihood ratio along with (counterintuitively) a positive result on achievability of testing. This strategy appears to be new even in the setting of unbounded computation, in which case it gives an alternate way to analyze the fundamental statistical limits of testing.