Learning Mixture Models via Efficient High-dimensional Sparse Fourier Transforms

In this work, we give a ${\rm poly}(d,k)$ time and sample algorithm for efficiently learning the parameters of a mixture of $k$ spherical distributions in $d$ dimensions. Unlike all previous methods, our techniques apply to heavy-tailed distributions and include examples that do not even have finite covariances. Our method succeeds whenever the cluster distributions have a characteristic function with sufficiently heavy tails. Such distributions include the Laplace distribution but crucially exclude Gaussians. All previous methods for learning mixture models relied implicitly or explicitly on the low-degree moments. Even for the case of Laplace distributions, we prove that any such algorithm must use super-polynomially many samples. Our method thus adds to the short list of techniques that bypass the limitations of the method of moments. Somewhat surprisingly, our algorithm does not require any minimum separation between the cluster means. This is in stark contrast to spherical Gaussian mixtures where a minimum $\ell_2$-separation is provably necessary even information-theoretically [Regev and Vijayaraghavan '17]. Our methods compose well with existing techniques and allow obtaining ''best of both worlds" guarantees for mixtures where every component either has a heavy-tailed characteristic function or has a sub-Gaussian tail with a light-tailed characteristic function. Our algorithm is based on a new approach to learning mixture models via efficient high-dimensional sparse Fourier transforms. We believe that this method will find more applications to statistical estimation. As an example, we give an algorithm for consistent robust mean estimation against noise-oblivious adversaries, a model practically motivated by the literature on multiple hypothesis testing. It was formally proposed in a recent Master's thesis by one of the authors, and has already inspired follow-up works.

Overcomplete Tensor Decomposition via Koszul-Young Flattenings

Motivated by connections between algebraic complexity lower bounds and tensor decompositions, we investigate Koszul-Young flattenings, which are the main ingredient in recent lower bounds for matrix multiplication. Based on this tool we give a new algorithm for decomposing an $n_1 \times n_2 \times n_3$ tensor as the sum of a minimal number of rank-1 terms, and certifying uniqueness of this decomposition. For $n_1 \le n_2 \le n_3$ with $n_1 \to \infty$ and $n_3/n_2 = O(1)$, our algorithm is guaranteed to succeed when the tensor rank is bounded by $r \le (1-\epsilon)(n_2 + n_3)$ for an arbitrary $\epsilon > 0$, provided the tensor components are generically chosen. For any fixed $\epsilon$, the runtime is polynomial in $n_3$. When $n_2 = n_3 = n$, our condition on the rank gives a factor-of-2 improvement over the classical simultaneous diagonalization algorithm, which requires $r \le n$, and also improves on the recent algorithm of Koiran (2024) which requires $r \le 4n/3$. It also improves on the PhD thesis of Persu (2018) which solves rank detection for $r \leq 3n/2$. We complement our upper bounds by showing limitations, in particular that no flattening of the style we consider can surpass rank $n_2 + n_3$. Furthermore, for $n \times n \times n$ tensors, we show that an even more general class of degree-$d$ polynomial flattenings cannot surpass rank $Cn$ for a constant $C = C(d)$. This suggests that for tensor decompositions, the case of generic components may be fundamentally harder than that of random components, where efficient decomposition is possible even in highly overcomplete settings.

Dimension Reduction via Sum-of-Squares and Improved Clustering Algorithms for Non-Spherical Mixtures

We develop a new approach for clustering non-spherical (i.e., arbitrary component covariances) Gaussian mixture models via a subroutine, based on the sum-of-squares method, that finds a low-dimensional separation-preserving projection of the input data. Our method gives a non-spherical analog of the classical dimension reduction, based on singular value decomposition, that forms a key component of the celebrated spherical clustering algorithm of Vempala and Wang [VW04] (in addition to several other applications). As applications, we obtain an algorithm to (1) cluster an arbitrary total-variation separated mixture of $k$ centered (i.e., zero-mean) Gaussians with $n\geq \operatorname{poly}(d) f(w_{\min}^{-1})$ samples and $\operatorname{poly}(n)$ time, and (2) cluster an arbitrary total-variation separated mixture of $k$ Gaussians with identical but arbitrary unknown covariance with $n \geq d^{O(\log w_{\min}^{-1})} f(w_{\min}^{-1})$ samples and $n^{O(\log w_{\min}^{-1})}$ time. Here, $w_{\min}$ is the minimum mixing weight of the input mixture, and $f$ does not depend on the dimension $d$. Our algorithms naturally extend to tolerating a dimension-independent fraction of arbitrary outliers. Before this work, the techniques in the state-of-the-art non-spherical clustering algorithms needed $d^{O(k)} f(w_{\min}^{-1})$ time and samples for clustering such mixtures. Our results may come as a surprise in the context of the $d^{\Omega(k)}$ statistical query lower bound [DKS17] for clustering non-spherical Gaussian mixtures. While this result is usually thought to rule out $d^{o(k)}$ cost algorithms for the problem, our results show that the lower bounds can in fact be circumvented for a remarkably general class of Gaussian mixtures.

Privately Estimating a Gaussian: Efficient, Robust and Optimal

In this work, we give efficient algorithms for privately estimating a Gaussian distribution in both pure and approximate differential privacy (DP) models with optimal dependence on the dimension in the sample complexity. In the pure DP setting, we give an efficient algorithm that estimates an unknown $d$-dimensional Gaussian distribution up to an arbitrary tiny total variation error using $\widetilde{O}(d^2 \log \kappa)$ samples while tolerating a constant fraction of adversarial outliers. Here, $\kappa$ is the condition number of the target covariance matrix. The sample bound matches best non-private estimators in the dependence on the dimension (up to a polylogarithmic factor). We prove a new lower bound on differentially private covariance estimation to show that the dependence on the condition number $\kappa$ in the above sample bound is also tight. Prior to our work, only identifiability results (yielding inefficient super-polynomial time algorithms) were known for the problem. In the approximate DP setting, we give an efficient algorithm to estimate an unknown Gaussian distribution up to an arbitrarily tiny total variation error using $\widetilde{O}(d^2)$ samples while tolerating a constant fraction of adversarial outliers. Prior to our work, all efficient approximate DP algorithms incurred a super-quadratic sample cost or were not outlier-robust. For the special case of mean estimation, our algorithm achieves the optimal sample complexity of $\widetilde O(d)$, improving on a $\widetilde O(d^{1.5})$ bound from prior work. Our pure DP algorithm relies on a recursive private preconditioning subroutine that utilizes the recent work on private mean estimation [Hopkins et al., 2022]. Our approximate DP algorithms are based on a substantial upgrade of the method of stabilizing convex relaxations introduced in [Kothari et al., 2022].

A Moment-Matching Approach to Testable Learning and a New Characterization of Rademacher Complexity

A remarkable recent paper by Rubinfeld and Vasilyan (2022) initiated the study of \emph{testable learning}, where the goal is to replace hard-to-verify distributional assumptions (such as Gaussianity) with efficiently testable ones and to require that the learner succeed whenever the unknown distribution passes the corresponding test. In this model, they gave an efficient algorithm for learning halfspaces under testable assumptions that are provably satisfied by Gaussians. In this paper we give a powerful new approach for developing algorithms for testable learning using tools from moment matching and metric distances in probability. We obtain efficient testable learners for any concept class that admits low-degree \emph{sandwiching polynomials}, capturing most important examples for which we have ordinary agnostic learners. We recover the results of Rubinfeld and Vasilyan as a corollary of our techniques while achieving improved, near-optimal sample complexity bounds for a broad range of concept classes and distributions. Surprisingly, we show that the information-theoretic sample complexity of testable learning is tightly characterized by the Rademacher complexity of the concept class, one of the most well-studied measures in statistical learning theory. In particular, uniform convergence is necessary and sufficient for testable learning. This leads to a fundamental separation from (ordinary) distribution-specific agnostic learning, where uniform convergence is sufficient but not necessary.

List-Decodable Covariance Estimation

We give the first polynomial time algorithm for \emph{list-decodable covariance estimation}. For any $\alpha > 0$, our algorithm takes input a sample $Y \subseteq \mathbb{R}^d$ of size $n\geq d^{\mathsf{poly}(1/\alpha)}$ obtained by adversarially corrupting an $(1-\alpha)n$ points in an i.i.d. sample $X$ of size $n$ from the Gaussian distribution with unknown mean $\mu_*$ and covariance $\Sigma_*$. In $n^{\mathsf{poly}(1/\alpha)}$ time, it outputs a constant-size list of $k = k(\alpha)= (1/\alpha)^{\mathsf{poly}(1/\alpha)}$ candidate parameters that, with high probability, contains a $(\hat{\mu},\hat{\Sigma})$ such that the total variation distance $TV(\mathcal{N}(\mu_*,\Sigma_*),\mathcal{N}(\hat{\mu},\hat{\Sigma}))<1-O_{\alpha}(1)$. This is the statistically strongest notion of distance and implies multiplicative spectral and relative Frobenius distance approximation for parameters with dimension independent error. Our algorithm works more generally for $(1-\alpha)$-corruptions of any distribution $D$ that possesses low-degree sum-of-squares certificates of two natural analytic properties: 1) anti-concentration of one-dimensional marginals and 2) hypercontractivity of degree 2 polynomials. Prior to our work, the only known results for estimating covariance in the list-decodable setting were for the special cases of list-decodable linear regression and subspace recovery due to Karmarkar, Klivans, and Kothari (2019), Raghavendra and Yau (2019 and 2020) and Bakshi and Kothari (2020). These results need superpolynomial time for obtaining any subconstant error in the underlying dimension. Our result implies the first polynomial-time \emph{exact} algorithm for list-decodable linear regression and subspace recovery that allows, in particular, to obtain $2^{-\mathsf{poly}(d)}$ error in polynomial-time. Our result also implies an improved algorithm for clustering non-spherical mixtures.

Private Robust Estimation by Stabilizing Convex Relaxations

We give the first polynomial time and sample $(\epsilon, \delta)$-differentially private (DP) algorithm to estimate the mean, covariance and higher moments in the presence of a constant fraction of adversarial outliers. Our algorithm succeeds for families of distributions that satisfy two well-studied properties in prior works on robust estimation: certifiable subgaussianity of directional moments and certifiable hypercontractivity of degree 2 polynomials. Our recovery guarantees hold in the "right affine-invariant norms": Mahalanobis distance for mean, multiplicative spectral and relative Frobenius distance guarantees for covariance and injective norms for higher moments. Prior works obtained private robust algorithms for mean estimation of subgaussian distributions with bounded covariance. For covariance estimation, ours is the first efficient algorithm (even in the absence of outliers) that succeeds without any condition-number assumptions. Our algorithms arise from a new framework that provides a general blueprint for modifying convex relaxations for robust estimation to satisfy strong worst-case stability guarantees in the appropriate parameter norms whenever the algorithms produce witnesses of correctness in their run. We verify such guarantees for a modification of standard sum-of-squares (SoS) semidefinite programming relaxations for robust estimation. Our privacy guarantees are obtained by combining stability guarantees with a new "estimate dependent" noise injection mechanism in which noise scales with the eigenvalues of the estimated covariance. We believe this framework will be useful more generally in obtaining DP counterparts of robust estimators. Independently of our work, Ashtiani and Liaw [AL21] also obtained a polynomial time and sample private robust estimation algorithm for Gaussian distributions.

Memory-Sample Lower Bounds for Learning Parity with Noise

In this work, we show, for the well-studied problem of learning parity under noise, where a learner tries to learn $x=(x_1,\ldots,x_n) \in \{0,1\}^n$ from a stream of random linear equations over $\mathrm{F}_2$ that are correct with probability $\frac{1}{2}+\varepsilon$ and flipped with probability $\frac{1}{2}-\varepsilon$, that any learning algorithm requires either a memory of size $\Omega(n^2/\varepsilon)$ or an exponential number of samples. In fact, we study memory-sample lower bounds for a large class of learning problems, as characterized by [GRT'18], when the samples are noisy. A matrix $M: A \times X \rightarrow \{-1,1\}$ corresponds to the following learning problem with error parameter $\varepsilon$: an unknown element $x \in X$ is chosen uniformly at random. A learner tries to learn $x$ from a stream of samples, $(a_1, b_1), (a_2, b_2) \ldots$, where for every $i$, $a_i \in A$ is chosen uniformly at random and $b_i = M(a_i,x)$ with probability $1/2+\varepsilon$ and $b_i = -M(a_i,x)$ with probability $1/2-\varepsilon$ ($0<\varepsilon< \frac{1}{2}$). Assume that $k,\ell, r$ are such that any submatrix of $M$ of at least $2^{-k} \cdot |A|$ rows and at least $2^{-\ell} \cdot |X|$ columns, has a bias of at most $2^{-r}$. We show that any learning algorithm for the learning problem corresponding to $M$, with error, requires either a memory of size at least $\Omega\left(\frac{k \cdot \ell}{\varepsilon} \right)$, or at least $2^{\Omega(r)}$ samples. In particular, this shows that for a large class of learning problems, same as those in [GRT'18], any learning algorithm requires either a memory of size at least $\Omega\left(\frac{(\log |X|) \cdot (\log |A|)}{\varepsilon}\right)$ or an exponential number of noisy samples. Our proof is based on adapting the arguments in [Raz'17,GRT'18] to the noisy case.

Robustly Learning Mixtures of $k$ Arbitrary Gaussians

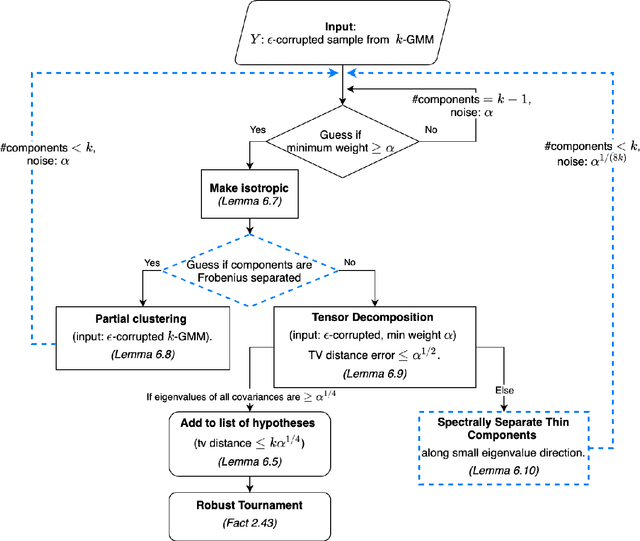
We give a polynomial-time algorithm for the problem of robustly estimating a mixture of $k$ arbitrary Gaussians in $\mathbb{R}^d$, for any fixed $k$, in the presence of a constant fraction of arbitrary corruptions. This resolves the main open problem in several previous works on algorithmic robust statistics, which addressed the special cases of robustly estimating (a) a single Gaussian, (b) a mixture of TV-distance separated Gaussians, and (c) a uniform mixture of two Gaussians. Our main tools are an efficient \emph{partial clustering} algorithm that relies on the sum-of-squares method, and a novel tensor decomposition algorithm that allows errors in both Frobenius norm and low-rank terms.

Sparse PCA: Algorithms, Adversarial Perturbations and Certificates

We study efficient algorithms for Sparse PCA in standard statistical models (spiked covariance in its Wishart form). Our goal is to achieve optimal recovery guarantees while being resilient to small perturbations. Despite a long history of prior works, including explicit studies of perturbation resilience, the best known algorithmic guarantees for Sparse PCA are fragile and break down under small adversarial perturbations. We observe a basic connection between perturbation resilience and \emph{certifying algorithms} that are based on certificates of upper bounds on sparse eigenvalues of random matrices. In contrast to other techniques, such certifying algorithms, including the brute-force maximum likelihood estimator, are automatically robust against small adversarial perturbation. We use this connection to obtain the first polynomial-time algorithms for this problem that are resilient against additive adversarial perturbations by obtaining new efficient certificates for upper bounds on sparse eigenvalues of random matrices. Our algorithms are based either on basic semidefinite programming or on its low-degree sum-of-squares strengthening depending on the parameter regimes. Their guarantees either match or approach the best known guarantees of \emph{fragile} algorithms in terms of sparsity of the unknown vector, number of samples and the ambient dimension. To complement our algorithmic results, we prove rigorous lower bounds matching the gap between fragile and robust polynomial-time algorithms in a natural computational model based on low-degree polynomials (closely related to the pseudo-calibration technique for sum-of-squares lower bounds) that is known to capture the best known guarantees for related statistical estimation problems. The combination of these results provides formal evidence of an inherent price to pay to achieve robustness.