Robust Sparse Regression with Non-Isotropic Designs

We develop a technique to design efficiently computable estimators for sparse linear regression in the simultaneous presence of two adversaries: oblivious and adaptive. We design several robust algorithms that outperform the state of the art even in the special case when oblivious adversary simply adds Gaussian noise. In particular, we provide a polynomial-time algorithm that with high probability recovers the signal up to error $O(\sqrt{\varepsilon})$ as long as the number of samples $n \ge \tilde{O}(k^2/\varepsilon)$, only assuming some bounds on the third and the fourth moments of the distribution ${D}$ of the design. In addition, prior to this work, even in the special case of Gaussian design and noise, no polynomial time algorithm was known to achieve error $o(\sqrt{\varepsilon})$ in the sparse setting $n < d^2$. We show that under some assumptions on the fourth and the eighth moments of ${D}$, there is a polynomial-time algorithm that achieves error $o(\sqrt{\varepsilon})$ as long as $n \ge \tilde{O}(k^4 / \varepsilon^3)$. For Gaussian distribution, this algorithm achieves error $O(\varepsilon^{3/4})$. Moreover, our algorithm achieves error $o(\sqrt{\varepsilon})$ for all log-concave distributions if $\varepsilon \le 1/\text{polylog(d)}$. Our algorithms are based on the filtering of the covariates that uses sum-of-squares relaxations, and weighted Huber loss minimization with $\ell_1$ regularizer. We provide a novel analysis of weighted penalized Huber loss that is suitable for heavy-tailed designs in the presence of two adversaries. Furthermore, we complement our algorithmic results with Statistical Query lower bounds, providing evidence that our estimators are likely to have nearly optimal sample complexity.

Robust Mixture Learning when Outliers Overwhelm Small Groups

We study the problem of estimating the means of well-separated mixtures when an adversary may add arbitrary outliers. While strong guarantees are available when the outlier fraction is significantly smaller than the minimum mixing weight, much less is known when outliers may crowd out low-weight clusters - a setting we refer to as list-decodable mixture learning (LD-ML). In this case, adversarial outliers can simulate additional spurious mixture components. Hence, if all means of the mixture must be recovered up to a small error in the output list, the list size needs to be larger than the number of (true) components. We propose an algorithm that obtains order-optimal error guarantees for each mixture mean with a minimal list-size overhead, significantly improving upon list-decodable mean estimation, the only existing method that is applicable for LD-ML. Although improvements are observed even when the mixture is non-separated, our algorithm achieves particularly strong guarantees when the mixture is separated: it can leverage the mixture structure to partially cluster the samples before carefully iterating a base learner for list-decodable mean estimation at different scales.

Robust Mean Estimation Without a Mean: Dimension-Independent Error in Polynomial Time for Symmetric Distributions

In this work, we study the problem of robustly estimating the mean/location parameter of distributions without moment bounds. For a large class of distributions satisfying natural symmetry constraints we give a sequence of algorithms that can efficiently estimate its location without incurring dimension-dependent factors in the error. Concretely, suppose an adversary can arbitrarily corrupt an $\varepsilon$-fraction of the observed samples. For every $k \in \mathbb{N}$, we design an estimator using time and samples $\tilde{O}({d^k})$ such that the dependence of the error on the corruption level $\varepsilon$ is an additive factor of $O(\varepsilon^{1-\frac{1}{2k}})$. The dependence on other problem parameters is also nearly optimal. Our class contains products of arbitrary symmetric one-dimensional distributions as well as elliptical distributions, a vast generalization of the Gaussian distribution. Examples include product Cauchy distributions and multi-variate $t$-distributions. In particular, even the first moment might not exist. We provide the first efficient algorithms for this class of distributions. Previously, such results where only known under boundedness assumptions on the moments of the distribution and in particular, are provably impossible in the absence of symmetry [KSS18, CTBJ22]. For the class of distributions we consider, all previous estimators either require exponential time or incur error depending on the dimension. Our algorithms are based on a generalization of the filtering technique [DK22]. We show how this machinery can be combined with Huber-loss-based approach to work with projections of the noise. Moreover, we show how sum-of-squares proofs can be used to obtain algorithmic guarantees even for distributions without first moment. We believe that this approach may find other application in future works.

Sparse PCA Beyond Covariance Thresholding

In the Wishart model for sparse PCA we are given $n$ samples $Y_1,\ldots, Y_n$ drawn independently from a $d$-dimensional Gaussian distribution $N({0, Id + \beta vv^\top})$, where $\beta > 0$ and $v\in \mathbb{R}^d$ is a $k$-sparse unit vector, and we wish to recover $v$ (up to sign). We show that if $n \ge \Omega(d)$, then for every $t \ll k$ there exists an algorithm running in time $n\cdot d^{O(t)}$ that solves this problem as long as \[ \beta \gtrsim \frac{k}{\sqrt{nt}}\sqrt{\ln({2 + td/k^2})}\,. \] Prior to this work, the best polynomial time algorithm in the regime $k\approx \sqrt{d}$, called \emph{Covariance Thresholding} (proposed in [KNV15a] and analyzed in [DM14]), required $\beta \gtrsim \frac{k}{\sqrt{n}}\sqrt{\ln({2 + d/k^2})}$. For large enough constant $t$ our algorithm runs in polynomial time and has better guarantees than Covariance Thresholding. Previously known algorithms with such guarantees required quasi-polynomial time $d^{O(\log d)}$. In addition, we show that our techniques work with sparse PCA with adversarial perturbations studied in [dKNS20]. This model generalizes not only sparse PCA, but also other problems studied in prior works, including the sparse planted vector problem. As a consequence, we provide polynomial time algorithms for the sparse planted vector problem that have better guarantees than the state of the art in some regimes. Our approach also works with the Wigner model for sparse PCA. Moreover, we show that it is possible to combine our techniques with recent results on sparse PCA with symmetric heavy-tailed noise [dNNS22]. In particular, in the regime $k \approx \sqrt{d}$ we get the first polynomial time algorithm that works with symmetric heavy-tailed noise, while the algorithm from [dNNS22]. requires quasi-polynomial time in these settings.

Higher degree sum-of-squares relaxations robust against oblivious outliers

We consider estimation models of the form $Y=X^*+N$, where $X^*$ is some $m$-dimensional signal we wish to recover, and $N$ is symmetrically distributed noise that may be unbounded in all but a small $\alpha$ fraction of the entries. We introduce a family of algorithms that under mild assumptions recover the signal $X^*$ in all estimation problems for which there exists a sum-of-squares algorithm that succeeds in recovering the signal $X^*$ when the noise $N$ is Gaussian. This essentially shows that it is enough to design a sum-of-squares algorithm for an estimation problem with Gaussian noise in order to get the algorithm that works with the symmetric noise model. Our framework extends far beyond previous results on symmetric noise models and is even robust to adversarial perturbations. As concrete examples, we investigate two problems for which no efficient algorithms were known to work for heavy-tailed noise: tensor PCA and sparse PCA. For the former, our algorithm recovers the principal component in polynomial time when the signal-to-noise ratio is at least $\tilde{O}(n^{p/4}/\alpha)$, that matches (up to logarithmic factors) current best known algorithmic guarantees for Gaussian noise. For the latter, our algorithm runs in quasipolynomial time and matches the state-of-the-art guarantees for quasipolynomial time algorithms in the case of Gaussian noise. Using a reduction from the planted clique problem, we provide evidence that the quasipolynomial time is likely to be necessary for sparse PCA with symmetric noise. In our proofs we use bounds on the covering numbers of sets of pseudo-expectations, which we obtain by certifying in sum-of-squares upper bounds on the Gaussian complexities of sets of solutions. This approach for bounding the covering numbers of sets of pseudo-expectations may be interesting in its own right and may find other application in future works.

Consistent Estimation for PCA and Sparse Regression with Oblivious Outliers

We develop machinery to design efficiently computable and consistent estimators, achieving estimation error approaching zero as the number of observations grows, when facing an oblivious adversary that may corrupt responses in all but an $\alpha$ fraction of the samples. As concrete examples, we investigate two problems: sparse regression and principal component analysis (PCA). For sparse regression, we achieve consistency for optimal sample size $n\gtrsim (k\log d)/\alpha^2$ and optimal error rate $O(\sqrt{(k\log d)/(n\cdot \alpha^2)})$ where $n$ is the number of observations, $d$ is the number of dimensions and $k$ is the sparsity of the parameter vector, allowing the fraction of inliers to be inverse-polynomial in the number of samples. Prior to this work, no estimator was known to be consistent when the fraction of inliers $\alpha$ is $o(1/\log \log n)$, even for (non-spherical) Gaussian design matrices. Results holding under weak design assumptions and in the presence of such general noise have only been shown in dense setting (i.e., general linear regression) very recently by d'Orsi et al. [dNS21]. In the context of PCA, we attain optimal error guarantees under broad spikiness assumptions on the parameter matrix (usually used in matrix completion). Previous works could obtain non-trivial guarantees only under the assumptions that the measurement noise corresponding to the inliers is polynomially small in $n$ (e.g., Gaussian with variance $1/n^2$). To devise our estimators, we equip the Huber loss with non-smooth regularizers such as the $\ell_1$ norm or the nuclear norm, and extend d'Orsi et al.'s approach [dNS21] in a novel way to analyze the loss function. Our machinery appears to be easily applicable to a wide range of estimation problems.

Sparse PCA: Algorithms, Adversarial Perturbations and Certificates

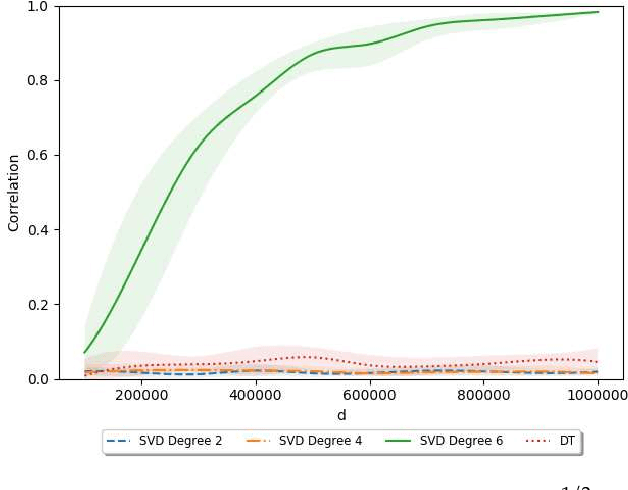
We study efficient algorithms for Sparse PCA in standard statistical models (spiked covariance in its Wishart form). Our goal is to achieve optimal recovery guarantees while being resilient to small perturbations. Despite a long history of prior works, including explicit studies of perturbation resilience, the best known algorithmic guarantees for Sparse PCA are fragile and break down under small adversarial perturbations. We observe a basic connection between perturbation resilience and \emph{certifying algorithms} that are based on certificates of upper bounds on sparse eigenvalues of random matrices. In contrast to other techniques, such certifying algorithms, including the brute-force maximum likelihood estimator, are automatically robust against small adversarial perturbation. We use this connection to obtain the first polynomial-time algorithms for this problem that are resilient against additive adversarial perturbations by obtaining new efficient certificates for upper bounds on sparse eigenvalues of random matrices. Our algorithms are based either on basic semidefinite programming or on its low-degree sum-of-squares strengthening depending on the parameter regimes. Their guarantees either match or approach the best known guarantees of \emph{fragile} algorithms in terms of sparsity of the unknown vector, number of samples and the ambient dimension. To complement our algorithmic results, we prove rigorous lower bounds matching the gap between fragile and robust polynomial-time algorithms in a natural computational model based on low-degree polynomials (closely related to the pseudo-calibration technique for sum-of-squares lower bounds) that is known to capture the best known guarantees for related statistical estimation problems. The combination of these results provides formal evidence of an inherent price to pay to achieve robustness.

Regress Consistently when Oblivious Outliers Overwhelm

We give a novel analysis of the Huber loss estimator for consistent robust linear regression proving that it simultaneously achieves an optimal dependency on the fraction of outliers and on the dimension. We consider a linear regression model with an oblivious adversary, who may corrupt the observations in an arbitrary way but without knowing the data. (This adversary model also captures heavy-tailed noise distributions). Given observations $y_1,\ldots,y_n$ with an $\alpha$ uncorrupted fraction, we obtain error guarantees $\tilde{O}(\sqrt{d/\alpha^2\cdot n})$, optimal up to logarithmic terms. Our algorithm works with a nearly optimal fraction of inliers $\alpha\geq \tilde{O}(\sqrt{d/n})$ and under mild restricted isometry assumptions (RIP) on the (transposed) design matrix. Prior to this work, even in the simple case of spherical Gaussian design, no estimator was known to achieve vanishing error guarantees in the high dimensional settings $d\gtrsim \sqrt{n}$, whenever the fraction of uncorrupted observations is smaller than $1/\log n$. Our analysis of the Huber loss estimator only exploits the first order optimality conditions. Furthermore, in the special case of Gaussian design $X\sim N(0,1)^{n \times d}$, we show that a strikingly simple algorithm based on computing coordinate-wise medians achieves similar guarantees in linear time. The algorithm also extends to the settings where the parameter vector $\beta^*$ is sparse.