Stefan Tiegel
Sample-Optimal Private Regression in Polynomial Time
Mar 31, 2025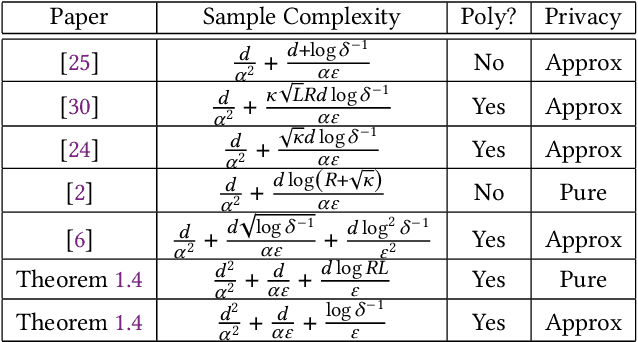
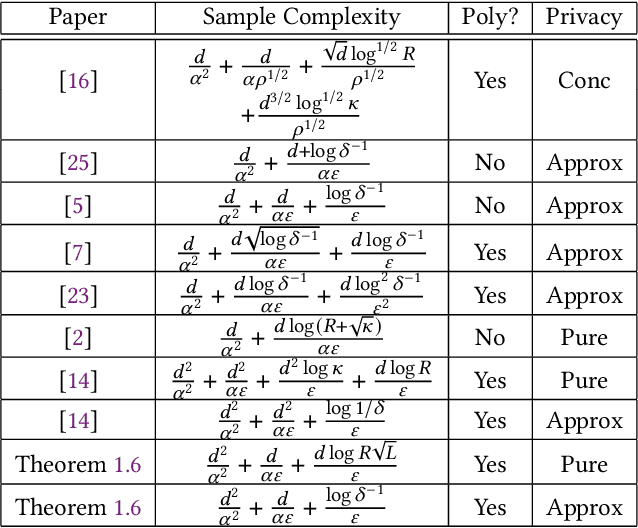
Abstract:We consider the task of privately obtaining prediction error guarantees in ordinary least-squares regression problems with Gaussian covariates (with unknown covariance structure). We provide the first sample-optimal polynomial time algorithm for this task under both pure and approximate differential privacy. We show that any improvement to the sample complexity of our algorithm would violate either statistical-query or information-theoretic lower bounds. Additionally, our algorithm is robust to a small fraction of arbitrary outliers and achieves optimal error rates as a function of the fraction of outliers. In contrast, all prior efficient algorithms either incurred sample complexities with sub-optimal dimension dependence, scaling with the condition number of the covariates, or obtained a polynomially worse dependence on the privacy parameters. Our technical contributions are two-fold: first, we leverage resilience guarantees of Gaussians within the sum-of-squares framework. As a consequence, we obtain efficient sum-of-squares algorithms for regression with optimal robustness rates and sample complexity. Second, we generalize the recent robustness-to-privacy framework [HKMN23, (arXiv:2212.05015)] to account for the geometry induced by the covariance of the input samples. This framework crucially relies on the robust estimators to be sum-of-squares algorithms, and combining the two steps yields a sample-optimal private regression algorithm. We believe our techniques are of independent interest, and we demonstrate this by obtaining an efficient algorithm for covariance-aware mean estimation, with an optimal dependence on the privacy parameters.
Improved Robust Estimation for Erdős-Rényi Graphs: The Sparse Regime and Optimal Breakdown Point
Mar 05, 2025Abstract:We study the problem of robustly estimating the edge density of Erd\H{o}s-R\'enyi random graphs $G(n, d^\circ/n)$ when an adversary can arbitrarily add or remove edges incident to an $\eta$-fraction of the nodes. We develop the first polynomial-time algorithm for this problem that estimates $d^\circ$ up to an additive error $O([\sqrt{\log(n) / n} + \eta\sqrt{\log(1/\eta)} ] \cdot \sqrt{d^\circ} + \eta \log(1/\eta))$. Our error guarantee matches information-theoretic lower bounds up to factors of $\log(1/\eta)$. Moreover, our estimator works for all $d^\circ \geq \Omega(1)$ and achieves optimal breakdown point $\eta = 1/2$. Previous algorithms [AJK+22, CDHS24], including inefficient ones, incur significantly suboptimal errors. Furthermore, even admitting suboptimal error guarantees, only inefficient algorithms achieve optimal breakdown point. Our algorithm is based on the sum-of-squares (SoS) hierarchy. A key ingredient is to construct constant-degree SoS certificates for concentration of the number of edges incident to small sets in $G(n, d^\circ/n)$. Crucially, we show that these certificates also exist in the sparse regime, when $d^\circ = o(\log n)$, a regime in which the performance of previous algorithms was significantly suboptimal.
SoS Certificates for Sparse Singular Values and Their Applications: Robust Statistics, Subspace Distortion, and More
Dec 30, 2024



Abstract:We study $\textit{sparse singular value certificates}$ for random rectangular matrices. If $M$ is an $n \times d$ matrix with independent Gaussian entries, we give a new family of polynomial-time algorithms which can certify upper bounds on the maximum of $\|M u\|$, where $u$ is a unit vector with at most $\eta n$ nonzero entries for a given $\eta \in (0,1)$. This basic algorithmic primitive lies at the heart of a wide range of problems across algorithmic statistics and theoretical computer science. Our algorithms certify a bound which is asymptotically smaller than the naive one, given by the maximum singular value of $M$, for nearly the widest-possible range of $n,d,$ and $\eta$. Efficiently certifying such a bound for a range of $n,d$ and $\eta$ which is larger by any polynomial factor than what is achieved by our algorithm would violate lower bounds in the SQ and low-degree polynomials models. Our certification algorithm makes essential use of the Sum-of-Squares hierarchy. To prove the correctness of our algorithm, we develop a new combinatorial connection between the graph matrix approach to analyze random matrices with dependent entries, and the Efron-Stein decomposition of functions of independent random variables. As applications of our certification algorithm, we obtain new efficient algorithms for a wide range of well-studied algorithmic tasks. In algorithmic robust statistics, we obtain new algorithms for robust mean and covariance estimation with tradeoffs between breakdown point and sample complexity, which are nearly matched by SQ and low-degree polynomial lower bounds (that we establish). We also obtain new polynomial-time guarantees for certification of $\ell_1/\ell_2$ distortion of random subspaces of $\mathbb{R}^n$ (also with nearly matching lower bounds), sparse principal component analysis, and certification of the $2\rightarrow p$ norm of a random matrix.
SoS Certifiability of Subgaussian Distributions and its Algorithmic Applications
Oct 28, 2024
Abstract:We prove that there is a universal constant $C>0$ so that for every $d \in \mathbb N$, every centered subgaussian distribution $\mathcal D$ on $\mathbb R^d$, and every even $p \in \mathbb N$, the $d$-variate polynomial $(Cp)^{p/2} \cdot \|v\|_{2}^p - \mathbb E_{X \sim \mathcal D} \langle v,X\rangle^p$ is a sum of square polynomials. This establishes that every subgaussian distribution is \emph{SoS-certifiably subgaussian} -- a condition that yields efficient learning algorithms for a wide variety of high-dimensional statistical tasks. As a direct corollary, we obtain computationally efficient algorithms with near-optimal guarantees for the following tasks, when given samples from an arbitrary subgaussian distribution: robust mean estimation, list-decodable mean estimation, clustering mean-separated mixture models, robust covariance-aware mean estimation, robust covariance estimation, and robust linear regression. Our proof makes essential use of Talagrand's generic chaining/majorizing measures theorem.
Robust Mixture Learning when Outliers Overwhelm Small Groups
Jul 22, 2024



Abstract:We study the problem of estimating the means of well-separated mixtures when an adversary may add arbitrary outliers. While strong guarantees are available when the outlier fraction is significantly smaller than the minimum mixing weight, much less is known when outliers may crowd out low-weight clusters - a setting we refer to as list-decodable mixture learning (LD-ML). In this case, adversarial outliers can simulate additional spurious mixture components. Hence, if all means of the mixture must be recovered up to a small error in the output list, the list size needs to be larger than the number of (true) components. We propose an algorithm that obtains order-optimal error guarantees for each mixture mean with a minimal list-size overhead, significantly improving upon list-decodable mean estimation, the only existing method that is applicable for LD-ML. Although improvements are observed even when the mixture is non-separated, our algorithm achieves particularly strong guarantees when the mixture is separated: it can leverage the mixture structure to partially cluster the samples before carefully iterating a base learner for list-decodable mean estimation at different scales.
Testably Learning Polynomial Threshold Functions
Jun 10, 2024Abstract:Rubinfeld & Vasilyan recently introduced the framework of testable learning as an extension of the classical agnostic model. It relaxes distributional assumptions which are difficult to verify by conditions that can be checked efficiently by a tester. The tester has to accept whenever the data truly satisfies the original assumptions, and the learner has to succeed whenever the tester accepts. We focus on the setting where the tester has to accept standard Gaussian data. There, it is known that basic concept classes such as halfspaces can be learned testably with the same time complexity as in the (distribution-specific) agnostic model. In this work, we ask whether there is a price to pay for testably learning more complex concept classes. In particular, we consider polynomial threshold functions (PTFs), which naturally generalize halfspaces. We show that PTFs of arbitrary constant degree can be testably learned up to excess error $\varepsilon > 0$ in time $n^{\mathrm{poly}(1/\varepsilon)}$. This qualitatively matches the best known guarantees in the agnostic model. Our results build on a connection between testable learning and fooling. In particular, we show that distributions that approximately match at least $\mathrm{poly}(1/\varepsilon)$ moments of the standard Gaussian fool constant-degree PTFs (up to error $\varepsilon$). As a secondary result, we prove that a direct approach to show testable learning (without fooling), which was successfully used for halfspaces, cannot work for PTFs.
Improved Hardness Results for Learning Intersections of Halfspaces
Feb 25, 2024Abstract:We show strong (and surprisingly simple) lower bounds for weakly learning intersections of halfspaces in the improper setting. Strikingly little is known about this problem. For instance, it is not even known if there is a polynomial-time algorithm for learning the intersection of only two halfspaces. On the other hand, lower bounds based on well-established assumptions (such as approximating worst-case lattice problems or variants of Feige's 3SAT hypothesis) are only known (or are implied by existing results) for the intersection of super-logarithmically many halfspaces [KS09,KS06,DSS16]. With intersections of fewer halfspaces being only ruled out under less standard assumptions [DV21] (such as the existence of local pseudo-random generators with large stretch). We significantly narrow this gap by showing that even learning $\omega(\log \log N)$ halfspaces in dimension $N$ takes super-polynomial time under standard assumptions on worst-case lattice problems (namely that SVP and SIVP are hard to approximate within polynomial factors). Further, we give unconditional hardness results in the statistical query framework. Specifically, we show that for any $k$ (even constant), learning $k$ halfspaces in dimension $N$ requires accuracy $N^{-\Omega(k)}$, or exponentially many queries -- in particular ruling out SQ algorithms with polynomial accuracy for $\omega(1)$ halfspaces. To the best of our knowledge this is the first unconditional hardness result for learning a super-constant number of halfspaces. Our lower bounds are obtained in a unified way via a novel connection we make between intersections of halfspaces and the so-called parallel pancakes distribution [DKS17,BLPR19,BRST21] that has been at the heart of many lower bound constructions in (robust) high-dimensional statistics in the past few years.
Computational-Statistical Gaps for Improper Learning in Sparse Linear Regression
Feb 21, 2024Abstract:We study computational-statistical gaps for improper learning in sparse linear regression. More specifically, given $n$ samples from a $k$-sparse linear model in dimension $d$, we ask what is the minimum sample complexity to efficiently (in time polynomial in $d$, $k$, and $n$) find a potentially dense estimate for the regression vector that achieves non-trivial prediction error on the $n$ samples. Information-theoretically this can be achieved using $\Theta(k \log (d/k))$ samples. Yet, despite its prominence in the literature, there is no polynomial-time algorithm known to achieve the same guarantees using less than $\Theta(d)$ samples without additional restrictions on the model. Similarly, existing hardness results are either restricted to the proper setting, in which the estimate must be sparse as well, or only apply to specific algorithms. We give evidence that efficient algorithms for this task require at least (roughly) $\Omega(k^2)$ samples. In particular, we show that an improper learning algorithm for sparse linear regression can be used to solve sparse PCA problems (with a negative spike) in their Wishart form, in regimes in which efficient algorithms are widely believed to require at least $\Omega(k^2)$ samples. We complement our reduction with low-degree and statistical query lower bounds for the sparse PCA problems from which we reduce. Our hardness results apply to the (correlated) random design setting in which the covariates are drawn i.i.d. from a mean-zero Gaussian distribution with unknown covariance.
Robust Mean Estimation Without a Mean: Dimension-Independent Error in Polynomial Time for Symmetric Distributions
Feb 21, 2023Abstract:In this work, we study the problem of robustly estimating the mean/location parameter of distributions without moment bounds. For a large class of distributions satisfying natural symmetry constraints we give a sequence of algorithms that can efficiently estimate its location without incurring dimension-dependent factors in the error. Concretely, suppose an adversary can arbitrarily corrupt an $\varepsilon$-fraction of the observed samples. For every $k \in \mathbb{N}$, we design an estimator using time and samples $\tilde{O}({d^k})$ such that the dependence of the error on the corruption level $\varepsilon$ is an additive factor of $O(\varepsilon^{1-\frac{1}{2k}})$. The dependence on other problem parameters is also nearly optimal. Our class contains products of arbitrary symmetric one-dimensional distributions as well as elliptical distributions, a vast generalization of the Gaussian distribution. Examples include product Cauchy distributions and multi-variate $t$-distributions. In particular, even the first moment might not exist. We provide the first efficient algorithms for this class of distributions. Previously, such results where only known under boundedness assumptions on the moments of the distribution and in particular, are provably impossible in the absence of symmetry [KSS18, CTBJ22]. For the class of distributions we consider, all previous estimators either require exponential time or incur error depending on the dimension. Our algorithms are based on a generalization of the filtering technique [DK22]. We show how this machinery can be combined with Huber-loss-based approach to work with projections of the noise. Moreover, we show how sum-of-squares proofs can be used to obtain algorithmic guarantees even for distributions without first moment. We believe that this approach may find other application in future works.
Private estimation algorithms for stochastic block models and mixture models
Jan 11, 2023Abstract:We introduce general tools for designing efficient private estimation algorithms, in the high-dimensional settings, whose statistical guarantees almost match those of the best known non-private algorithms. To illustrate our techniques, we consider two problems: recovery of stochastic block models and learning mixtures of spherical Gaussians. For the former, we present the first efficient $(\epsilon, \delta)$-differentially private algorithm for both weak recovery and exact recovery. Previously known algorithms achieving comparable guarantees required quasi-polynomial time. For the latter, we design an $(\epsilon, \delta)$-differentially private algorithm that recovers the centers of the $k$-mixture when the minimum separation is at least $ O(k^{1/t}\sqrt{t})$. For all choices of $t$, this algorithm requires sample complexity $n\geq k^{O(1)}d^{O(t)}$ and time complexity $(nd)^{O(t)}$. Prior work required minimum separation at least $O(\sqrt{k})$ as well as an explicit upper bound on the Euclidean norm of the centers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge