Retraining with Predicted Hard Labels Provably Increases Model Accuracy

The performance of a model trained with \textit{noisy labels} is often improved by simply \textit{retraining} the model with its own predicted \textit{hard} labels (i.e., $1$/$0$ labels). Yet, a detailed theoretical characterization of this phenomenon is lacking. In this paper, we theoretically analyze retraining in a linearly separable setting with randomly corrupted labels given to us and prove that retraining can improve the population accuracy obtained by initially training with the given (noisy) labels. To the best of our knowledge, this is the first such theoretical result. Retraining finds application in improving training with label differential privacy (DP) which involves training with noisy labels. We empirically show that retraining selectively on the samples for which the predicted label matches the given label significantly improves label DP training at \textit{no extra privacy cost}; we call this \textit{consensus-based retraining}. For e.g., when training ResNet-18 on CIFAR-100 with $\epsilon=3$ label DP, we obtain $6.4\%$ improvement in accuracy with consensus-based retraining.

Perturb-and-Project: Differentially Private Similarities and Marginals

We revisit the input perturbations framework for differential privacy where noise is added to the input $A\in \mathcal{S}$ and the result is then projected back to the space of admissible datasets $\mathcal{S}$. Through this framework, we first design novel efficient algorithms to privately release pair-wise cosine similarities. Second, we derive a novel algorithm to compute $k$-way marginal queries over $n$ features. Prior work could achieve comparable guarantees only for $k$ even. Furthermore, we extend our results to $t$-sparse datasets, where our efficient algorithms yields novel, stronger guarantees whenever $t\le n^{5/6}/\log n\,.$ Finally, we provide a theoretical perspective on why \textit{fast} input perturbation algorithms works well in practice. The key technical ingredients behind our results are tight sum-of-squares certificates upper bounding the Gaussian complexity of sets of solutions.

A Scalable Algorithm for Individually Fair K-means Clustering

We present a scalable algorithm for the individually fair ($p$, $k$)-clustering problem introduced by Jung et al. and Mahabadi et al. Given $n$ points $P$ in a metric space, let $\delta(x)$ for $x\in P$ be the radius of the smallest ball around $x$ containing at least $n / k$ points. A clustering is then called individually fair if it has centers within distance $\delta(x)$ of $x$ for each $x\in P$. While good approximation algorithms are known for this problem no efficient practical algorithms with good theoretical guarantees have been presented. We design the first fast local-search algorithm that runs in ~$O(nk^2)$ time and obtains a bicriteria $(O(1), 6)$ approximation. Then we show empirically that not only is our algorithm much faster than prior work, but it also produces lower-cost solutions.

Differentially Private Clustering in Data Streams

The streaming model is an abstraction of computing over massive data streams, which is a popular way of dealing with large-scale modern data analysis. In this model, there is a stream of data points, one after the other. A streaming algorithm is only allowed one pass over the data stream, and the goal is to perform some analysis during the stream while using as small space as possible. Clustering problems (such as $k$-means and $k$-median) are fundamental unsupervised machine learning primitives, and streaming clustering algorithms have been extensively studied in the past. However, since data privacy becomes a central concern in many real-world applications, non-private clustering algorithms are not applicable in many scenarios. In this work, we provide the first differentially private streaming algorithms for $k$-means and $k$-median clustering of $d$-dimensional Euclidean data points over a stream with length at most $T$ using $poly(k,d,\log(T))$ space to achieve a {\it constant} multiplicative error and a $poly(k,d,\log(T))$ additive error. In particular, we present a differentially private streaming clustering framework which only requires an offline DP coreset algorithm as a blackbox. By plugging in existing DP coreset results via Ghazi, Kumar, Manurangsi 2020 and Kaplan, Stemmer 2018, we achieve (1) a $(1+\gamma)$-multiplicative approximation with $\tilde{O}_\gamma(poly(k,d,\log(T)))$ space for any $\gamma>0$, and the additive error is $poly(k,d,\log(T))$ or (2) an $O(1)$-multiplicative approximation with $\tilde{O}(k \cdot poly(d,\log(T)))$ space and $poly(k,d,\log(T))$ additive error. In addition, our algorithmic framework is also differentially private under the continual release setting, i.e., the union of outputs of our algorithms at every timestamp is always differentially private.

Measuring Re-identification Risk

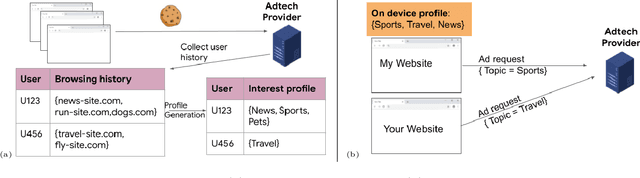
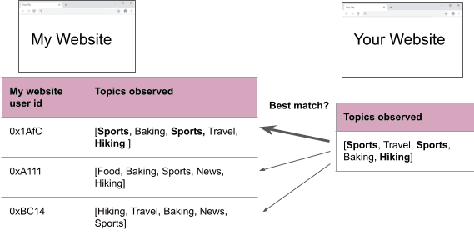
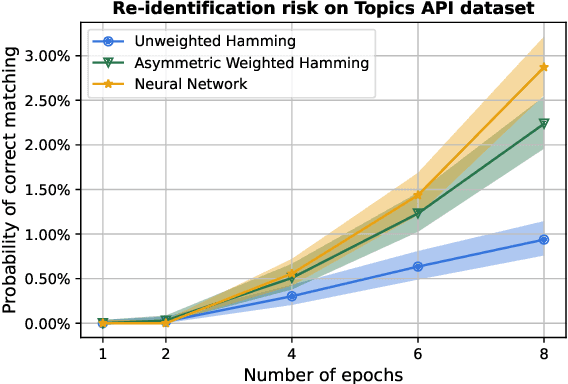
Compact user representations (such as embeddings) form the backbone of personalization services. In this work, we present a new theoretical framework to measure re-identification risk in such user representations. Our framework, based on hypothesis testing, formally bounds the probability that an attacker may be able to obtain the identity of a user from their representation. As an application, we show how our framework is general enough to model important real-world applications such as the Chrome's Topics API for interest-based advertising. We complement our theoretical bounds by showing provably good attack algorithms for re-identification that we use to estimate the re-identification risk in the Topics API. We believe this work provides a rigorous and interpretable notion of re-identification risk and a framework to measure it that can be used to inform real-world applications.

Differentially-Private Hierarchical Clustering with Provable Approximation Guarantees

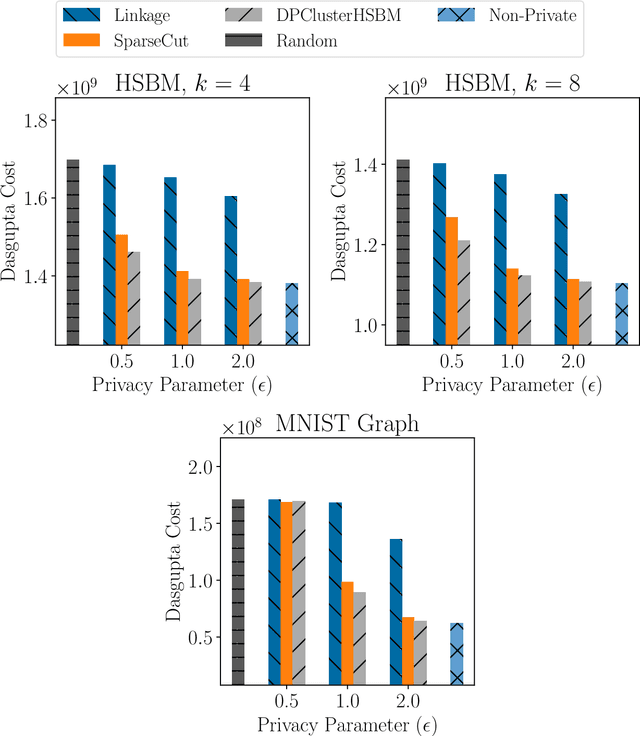
Hierarchical Clustering is a popular unsupervised machine learning method with decades of history and numerous applications. We initiate the study of differentially private approximation algorithms for hierarchical clustering under the rigorous framework introduced by (Dasgupta, 2016). We show strong lower bounds for the problem: that any $\epsilon$-DP algorithm must exhibit $O(|V|^2/ \epsilon)$-additive error for an input dataset $V$. Then, we exhibit a polynomial-time approximation algorithm with $O(|V|^{2.5}/ \epsilon)$-additive error, and an exponential-time algorithm that meets the lower bound. To overcome the lower bound, we focus on the stochastic block model, a popular model of graphs, and, with a separation assumption on the blocks, propose a private $1+o(1)$ approximation algorithm which also recovers the blocks exactly. Finally, we perform an empirical study of our algorithms and validate their performance.

Private estimation algorithms for stochastic block models and mixture models

We introduce general tools for designing efficient private estimation algorithms, in the high-dimensional settings, whose statistical guarantees almost match those of the best known non-private algorithms. To illustrate our techniques, we consider two problems: recovery of stochastic block models and learning mixtures of spherical Gaussians. For the former, we present the first efficient $(\epsilon, \delta)$-differentially private algorithm for both weak recovery and exact recovery. Previously known algorithms achieving comparable guarantees required quasi-polynomial time. For the latter, we design an $(\epsilon, \delta)$-differentially private algorithm that recovers the centers of the $k$-mixture when the minimum separation is at least $ O(k^{1/t}\sqrt{t})$. For all choices of $t$, this algorithm requires sample complexity $n\geq k^{O(1)}d^{O(t)}$ and time complexity $(nd)^{O(t)}$. Prior work required minimum separation at least $O(\sqrt{k})$ as well as an explicit upper bound on the Euclidean norm of the centers.

Differentially Private Graph Learning via Sensitivity-Bounded Personalized PageRank

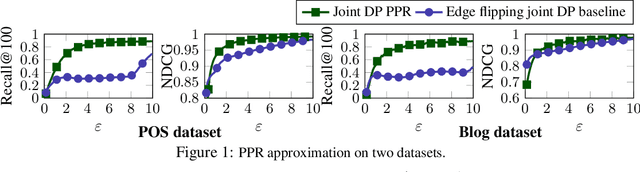
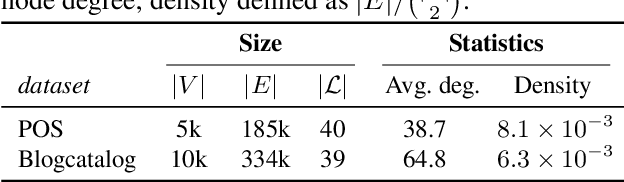
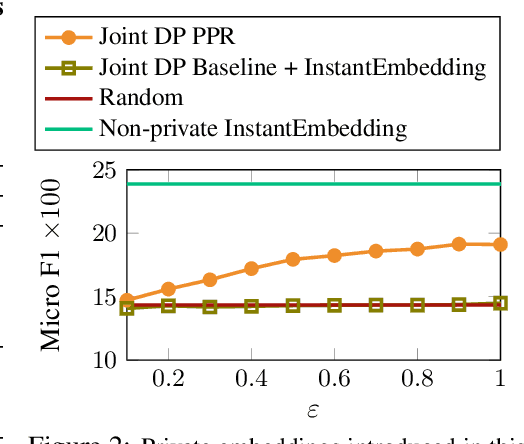
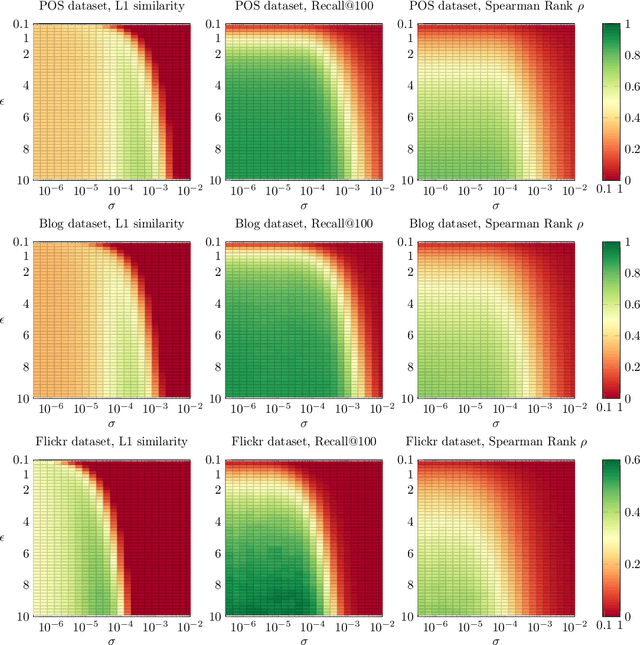
Personalized PageRank (PPR) is a fundamental tool in unsupervised learning of graph representations such as node ranking, labeling, and graph embedding. However, while data privacy is one of the most important recent concerns, existing PPR algorithms are not designed to protect user privacy. PPR is highly sensitive to the input graph edges: the difference of only one edge may cause a big change in the PPR vector, potentially leaking private user data. In this work, we propose an algorithm which outputs an approximate PPR and has provably bounded sensitivity to input edges. In addition, we prove that our algorithm achieves similar accuracy to non-private algorithms when the input graph has large degrees. Our sensitivity-bounded PPR directly implies private algorithms for several tools of graph learning, such as, differentially private (DP) PPR ranking, DP node classification, and DP node embedding. To complement our theoretical analysis, we also empirically verify the practical performances of our algorithms.

Smooth Anonymity for Sparse Binary Matrices

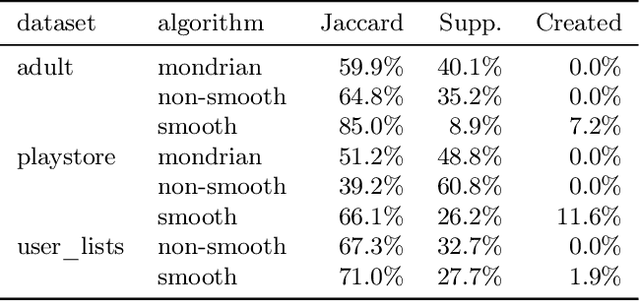
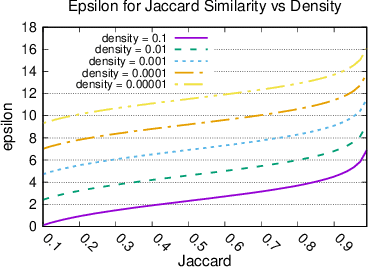
When working with user data providing well-defined privacy guarantees is paramount. In this work we aim to manipulate and share an entire sparse dataset with a third party privately. In fact, differential privacy has emerged as the gold standard of privacy, however, when it comes to sharing sparse datasets, as one of our main results, we prove that \emph{any} differentially private mechanism that maintains a reasonable similarity with the initial dataset is doomed to have a very weak privacy guarantee. Hence we need to opt for other privacy notions such as $k$-anonymity are better at preserving utility in this context. In this work we present a variation of $k$-anonymity, which we call smooth $k$-anonymity and design simple algorithms that efficiently provide smooth $k$-anonymity. We further perform an empirical evaluation to back our theoretical guarantees, and show that our algorithm improves the performance in downstream machine learning tasks on anonymized data.

Scalable Differentially Private Clustering via Hierarchically Separated Trees

We study the private $k$-median and $k$-means clustering problem in $d$ dimensional Euclidean space. By leveraging tree embeddings, we give an efficient and easy to implement algorithm, that is empirically competitive with state of the art non private methods. We prove that our method computes a solution with cost at most $O(d^{3/2}\log n)\cdot OPT + O(k d^2 \log^2 n / \epsilon^2)$, where $\epsilon$ is the privacy guarantee. (The dimension term, $d$, can be replaced with $O(\log k)$ using standard dimension reduction techniques.) Although the worst-case guarantee is worse than that of state of the art private clustering methods, the algorithm we propose is practical, runs in near-linear, $\tilde{O}(nkd)$, time and scales to tens of millions of points. We also show that our method is amenable to parallelization in large-scale distributed computing environments. In particular we show that our private algorithms can be implemented in logarithmic number of MPC rounds in the sublinear memory regime. Finally, we complement our theoretical analysis with an empirical evaluation demonstrating the algorithm's efficiency and accuracy in comparison to other privacy clustering baselines.