AI-rithmetic

Modern AI systems have been successfully deployed to win medals at international math competitions, assist with research workflows, and prove novel technical lemmas. However, despite their progress at advanced levels of mathematics, they remain stubbornly bad at basic arithmetic, consistently failing on the simple task of adding two numbers. We present a systematic investigation of this phenomenon. We demonstrate empirically that all frontier models suffer significantly degraded accuracy for integer addition as the number of digits increases. Furthermore, we show that most errors made by these models are highly interpretable and can be attributed to either operand misalignment or a failure to correctly carry; these two error classes explain 87.9%, 62.9%, and 92.4% of Claude Opus 4.1, GPT-5, and Gemini 2.5 Pro errors, respectively. Finally, we show that misalignment errors are frequently related to tokenization, and that carrying errors appear largely as independent random failures.

Optimal Learning from Label Proportions with General Loss Functions

Motivated by problems in online advertising, we address the task of Learning from Label Proportions (LLP). In this partially-supervised setting, training data consists of groups of examples, termed bags, for which we only observe the average label value. The main goal, however, remains the design of a predictor for the labels of individual examples. We introduce a novel and versatile low-variance de-biasing methodology to learn from aggregate label information, significantly advancing the state of the art in LLP. Our approach exhibits remarkable flexibility, seamlessly accommodating a broad spectrum of practically relevant loss functions across both binary and multi-class classification settings. By carefully combining our estimators with standard techniques, we substantially improve sample complexity guarantees for a large class of losses of practical relevance. We also empirically validate the efficacy of our proposed approach across a diverse array of benchmark datasets, demonstrating compelling empirical advantages over standard baselines.

Nearly Optimal Sample Complexity for Learning with Label Proportions

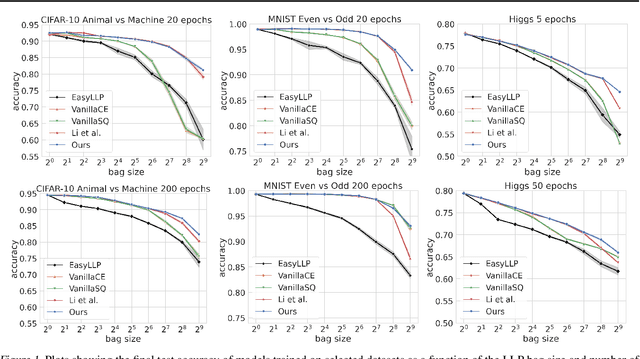
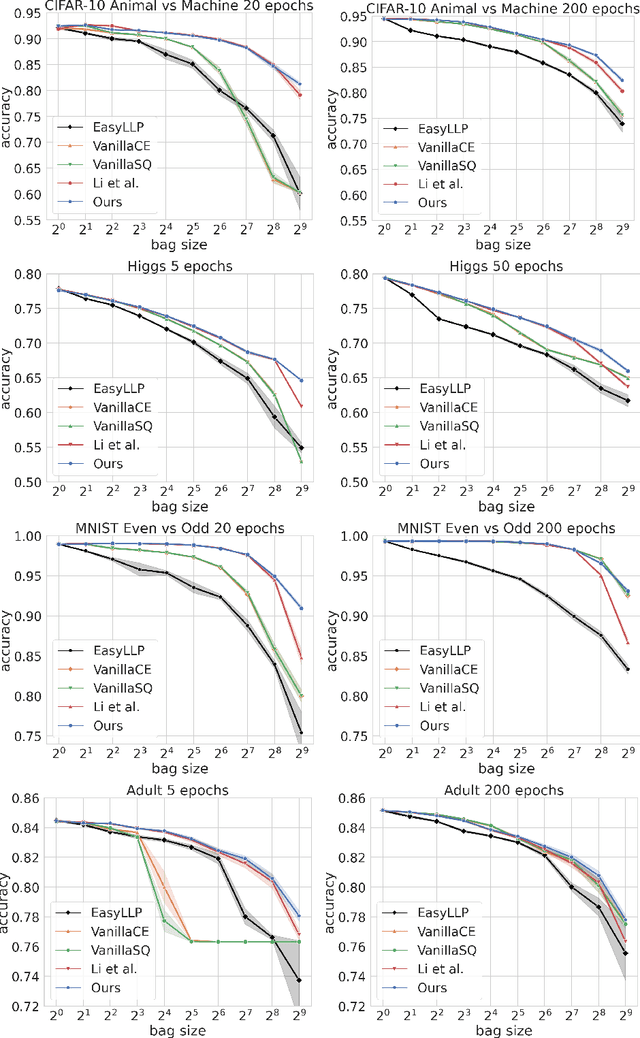
We investigate Learning from Label Proportions (LLP), a partial information setting where examples in a training set are grouped into bags, and only aggregate label values in each bag are available. Despite the partial observability, the goal is still to achieve small regret at the level of individual examples. We give results on the sample complexity of LLP under square loss, showing that our sample complexity is essentially optimal. From an algorithmic viewpoint, we rely on carefully designed variants of Empirical Risk Minimization, and Stochastic Gradient Descent algorithms, combined with ad hoc variance reduction techniques. On one hand, our theoretical results improve in important ways on the existing literature on LLP, specifically in the way the sample complexity depends on the bag size. On the other hand, we validate our algorithmic solutions on several datasets, demonstrating improved empirical performance (better accuracy for less samples) against recent baselines.

Auditing Privacy Mechanisms via Label Inference Attacks

We propose reconstruction advantage measures to audit label privatization mechanisms. A reconstruction advantage measure quantifies the increase in an attacker's ability to infer the true label of an unlabeled example when provided with a private version of the labels in a dataset (e.g., aggregate of labels from different users or noisy labels output by randomized response), compared to an attacker that only observes the feature vectors, but may have prior knowledge of the correlation between features and labels. We consider two such auditing measures: one additive, and one multiplicative. These incorporate previous approaches taken in the literature on empirical auditing and differential privacy. The measures allow us to place a variety of proposed privatization schemes -- some differentially private, some not -- on the same footing. We analyze these measures theoretically under a distributional model which encapsulates reasonable adversarial settings. We also quantify their behavior empirically on real and simulated prediction tasks. Across a range of experimental settings, we find that differentially private schemes dominate or match the privacy-utility tradeoff of more heuristic approaches.

Better Private Linear Regression Through Better Private Feature Selection

Existing work on differentially private linear regression typically assumes that end users can precisely set data bounds or algorithmic hyperparameters. End users often struggle to meet these requirements without directly examining the data (and violating privacy). Recent work has attempted to develop solutions that shift these burdens from users to algorithms, but they struggle to provide utility as the feature dimension grows. This work extends these algorithms to higher-dimensional problems by introducing a differentially private feature selection method based on Kendall rank correlation. We prove a utility guarantee for the setting where features are normally distributed and conduct experiments across 25 datasets. We find that adding this private feature selection step before regression significantly broadens the applicability of ``plug-and-play'' private linear regression algorithms at little additional cost to privacy, computation, or decision-making by the end user.

Measuring Re-identification Risk

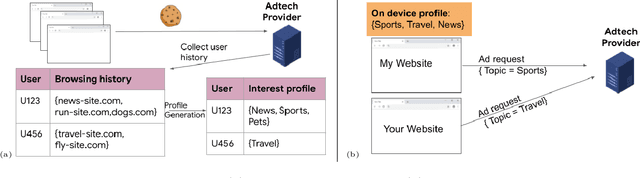
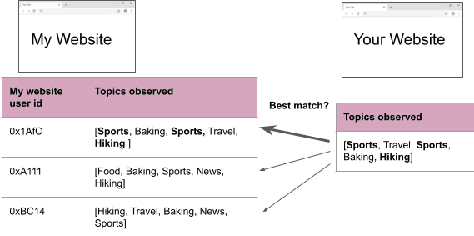
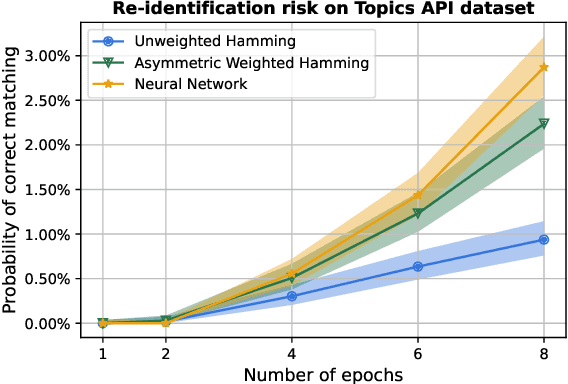
Compact user representations (such as embeddings) form the backbone of personalization services. In this work, we present a new theoretical framework to measure re-identification risk in such user representations. Our framework, based on hypothesis testing, formally bounds the probability that an attacker may be able to obtain the identity of a user from their representation. As an application, we show how our framework is general enough to model important real-world applications such as the Chrome's Topics API for interest-based advertising. We complement our theoretical bounds by showing provably good attack algorithms for re-identification that we use to estimate the re-identification risk in the Topics API. We believe this work provides a rigorous and interpretable notion of re-identification risk and a framework to measure it that can be used to inform real-world applications.

Subset-Based Instance Optimality in Private Estimation

We propose a new definition of instance optimality for differentially private estimation algorithms. Our definition requires an optimal algorithm to compete, simultaneously for every dataset $D$, with the best private benchmark algorithm that (a) knows $D$ in advance and (b) is evaluated by its worst-case performance on large subsets of $D$. That is, the benchmark algorithm need not perform well when potentially extreme points are added to $D$; it only has to handle the removal of a small number of real data points that already exist. This makes our benchmark significantly stronger than those proposed in prior work. We nevertheless show, for real-valued datasets, how to construct private algorithms that achieve our notion of instance optimality when estimating a broad class of dataset properties, including means, quantiles, and $\ell_p$-norm minimizers. For means in particular, we provide a detailed analysis and show that our algorithm simultaneously matches or exceeds the asymptotic performance of existing algorithms under a range of distributional assumptions.

Easy Learning from Label Proportions

We consider the problem of Learning from Label Proportions (LLP), a weakly supervised classification setup where instances are grouped into "bags", and only the frequency of class labels at each bag is available. Albeit, the objective of the learner is to achieve low task loss at an individual instance level. Here we propose Easyllp: a flexible and simple-to-implement debiasing approach based on aggregate labels, which operates on arbitrary loss functions. Our technique allows us to accurately estimate the expected loss of an arbitrary model at an individual level. We showcase the flexibility of our approach by applying it to popular learning frameworks, like Empirical Risk Minimization (ERM) and Stochastic Gradient Descent (SGD) with provable guarantees on instance level performance. More concretely, we exhibit a variance reduction technique that makes the quality of LLP learning deteriorate only by a factor of k (k being bag size) in both ERM and SGD setups, as compared to full supervision. Finally, we validate our theoretical results on multiple datasets demonstrating our algorithm performs as well or better than previous LLP approaches in spite of its simplicity.

Confidence-Ranked Reconstruction of Census Microdata from Published Statistics

A reconstruction attack on a private dataset $D$ takes as input some publicly accessible information about the dataset and produces a list of candidate elements of $D$. We introduce a new class of data reconstruction attacks based on randomized methods for non-convex optimization. We empirically demonstrate that our attacks can not only reconstruct full rows of $D$ from aggregate query statistics $Q(D)\in \mathbb{R}^m$, but can do so in a way that reliably ranks reconstructed rows by their odds of appearing in the private data, providing a signature that could be used for prioritizing reconstructed rows for further actions such as identify theft or hate crime. We also design a sequence of baselines for evaluating reconstruction attacks. Our attacks significantly outperform those that are based only on access to a public distribution or population from which the private dataset $D$ was sampled, demonstrating that they are exploiting information in the aggregate statistics $Q(D)$, and not simply the overall structure of the distribution. In other words, the queries $Q(D)$ are permitting reconstruction of elements of this dataset, not the distribution from which $D$ was drawn. These findings are established both on 2010 U.S. decennial Census data and queries and Census-derived American Community Survey datasets. Taken together, our methods and experiments illustrate the risks in releasing numerically precise aggregate statistics of a large dataset, and provide further motivation for the careful application of provably private techniques such as differential privacy.

Private Algorithms with Private Predictions

When applying differential privacy to sensitive data, a common way of getting improved performance is to use external information such as other sensitive data, public data, or human priors. We propose to use the algorithms with predictions framework -- previously applied largely to improve time complexity or competitive ratios -- as a powerful way of designing and analyzing privacy-preserving methods that can take advantage of such external information to improve utility. For four important tasks -- quantile release, its extension to multiple quantiles, covariance estimation, and data release -- we construct prediction-dependent differentially private methods whose utility scales with natural measures of prediction quality. The analyses enjoy several advantages, including minimal assumptions about the data, natural ways of adding robustness to noisy predictions, and novel "meta" algorithms that can learn predictions from other (potentially sensitive) data. Overall, our results demonstrate how to enable differentially private algorithms to make use of and learn noisy predictions, which holds great promise for improving utility while preserving privacy across a variety of tasks.