Efficient and Asymptotically Unbiased Constrained Decoding for Large Language Models

In real-world applications of large language models, outputs are often required to be confined: selecting items from predefined product or document sets, generating phrases that comply with safety standards, or conforming to specialized formatting styles. To control the generation, constrained decoding has been widely adopted. However, existing prefix-tree-based constrained decoding is inefficient under GPU-based model inference paradigms, and it introduces unintended biases into the output distribution. This paper introduces Dynamic Importance Sampling for Constrained Decoding (DISC) with GPU-based Parallel Prefix-Verification (PPV), a novel algorithm that leverages dynamic importance sampling to achieve theoretically guaranteed asymptotic unbiasedness and overcomes the inefficiency of prefix-tree. Extensive experiments demonstrate the superiority of our method over existing methods in both efficiency and output quality. These results highlight the potential of our methods to improve constrained generation in applications where adherence to specific constraints is essential.

Rate of Model Collapse in Recursive Training

Given the ease of creating synthetic data from machine learning models, new models can be potentially trained on synthetic data generated by previous models. This recursive training process raises concerns about the long-term impact on model quality. As models are recursively trained on generated data from previous rounds, their ability to capture the nuances of the original human-generated data may degrade. This is often referred to as \emph{model collapse}. In this work, we ask how fast model collapse occurs for some well-studied distribution families under maximum likelihood (ML or near ML) estimation during recursive training. Surprisingly, even for fundamental distributions such as discrete and Gaussian distributions, the exact rate of model collapse is unknown. In this work, we theoretically characterize the rate of collapse in these fundamental settings and complement it with experimental evaluations. Our results show that for discrete distributions, the time to forget a word is approximately linearly dependent on the number of times it occurred in the original corpus, and for Gaussian models, the standard deviation reduces to zero roughly at $n$ iterations, where $n$ is the number of samples at each iteration. Both of these findings imply that model forgetting, at least in these simple distributions under near ML estimation with many samples, takes a long time.

Coupling without Communication and Drafter-Invariant Speculative Decoding

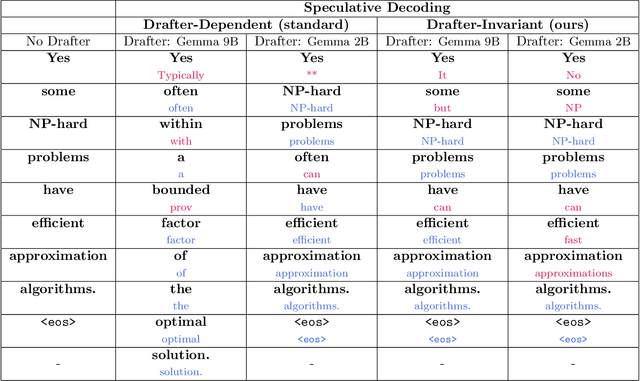
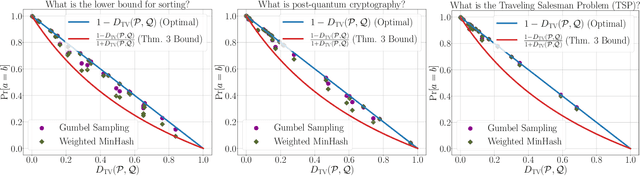
Suppose Alice has a distribution $P$ and Bob has a distribution $Q$. Alice wants to generate a sample $a\sim P$ and Bob a sample $b \sim Q$ such that $a = b$ with has as high of probability as possible. It is well-known that, by sampling from an optimal coupling between the distributions, Alice and Bob can achieve $Pr[a = b] = 1 - D_{TV}(P,Q)$, where $D_{TV}(P,Q)$ is the total variation distance. What if Alice and Bob must solve this same problem without communicating at all? Perhaps surprisingly, with access to public randomness, they can still achieve $Pr[a = b] \geq \frac{1 - D_{TV}(P,Q)}{1 + D_{TV}(P,Q)} \geq 1-2D_{TV}(P,Q)$. In fact, this bound can be obtained using a simple protocol based on the Weighted MinHash algorithm. In this work, we explore the communication-free coupling in greater depth. First, we show that an equally simple protocol based on Gumbel sampling matches the worst-case guarantees of the Weighted MinHash approach, but tends to perform better in practice. Conversely, we prove that both approaches are actually sharp: no communication-free protocol can achieve $Pr[a=b]>\frac{1 - D_{TV}(P,Q)}{1 + D_{TV}(P,Q)}$ in the worst-case. Finally, we prove that, for distributions over $n$ items, there exists a scheme that uses just $O(\log(n/\epsilon))$ bits of communication to achieve $Pr[a = b] = 1 - D_{TV}(P,Q) - \epsilon$, i.e. to essentially match optimal coupling. Beyond our theoretical results, we demonstrate an application of communication-free coupling to speculative decoding, a recent method for accelerating autoregressive large language models [Leviathan, Kalman, Matias, ICML 2023]. We show that communication-free protocols yield a variant of speculative decoding that we call Drafter-Invariant Speculative Decoding, which has the desirable property that the output of the method is fixed given a fixed random seed, regardless of what drafter is used for speculation.

Towards Fast Inference: Exploring and Improving Blockwise Parallel Drafts

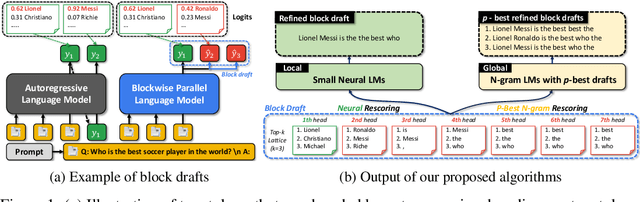
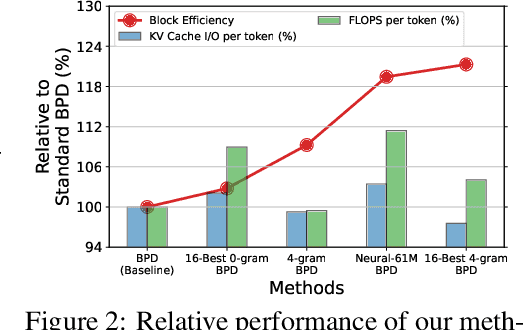
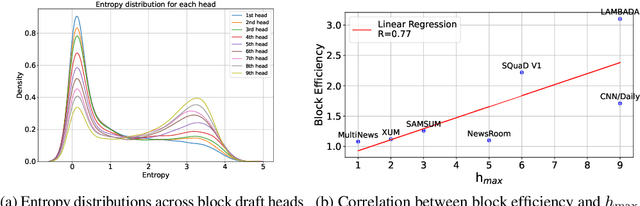
Despite the remarkable strides made by autoregressive language models, their potential is often hampered by the slow inference speeds inherent in sequential token generation. Blockwise parallel decoding (BPD) was proposed by Stern et al. (2018) as a way to improve inference speed of language models. In this paper, we make two contributions to understanding and improving BPD drafts. We first offer an analysis of the token distributions produced by the BPD prediction heads. Secondly, we use this analysis to inform algorithms to improve BPD inference speed by refining the BPD drafts using small n-gram or neural language models. We empirically show that these refined BPD drafts yield a higher average verified prefix length across tasks.

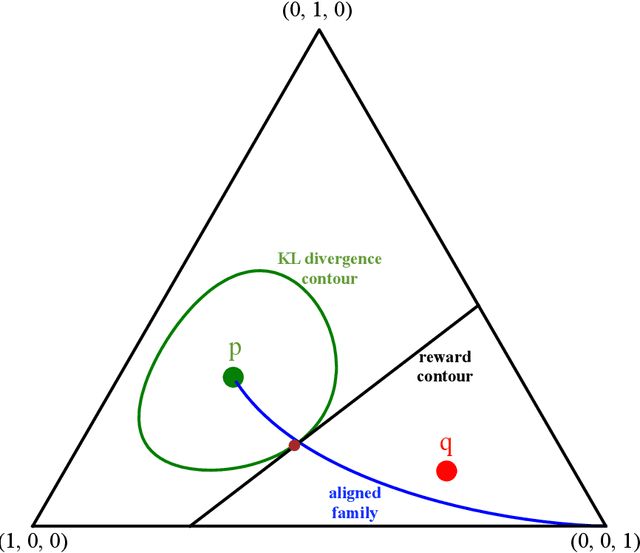
Asymptotics of Language Model Alignment

Let $p$ denote a generative language model. Let $r$ denote a reward model that returns a scalar that captures the degree at which a draw from $p$ is preferred. The goal of language model alignment is to alter $p$ to a new distribution $\phi$ that results in a higher expected reward while keeping $\phi$ close to $p.$ A popular alignment method is the KL-constrained reinforcement learning (RL), which chooses a distribution $\phi_\Delta$ that maximizes $E_{\phi_{\Delta}} r(y)$ subject to a relative entropy constraint $KL(\phi_\Delta || p) \leq \Delta.$ Another simple alignment method is best-of-$N$, where $N$ samples are drawn from $p$ and one with highest reward is selected. In this paper, we offer a closed-form characterization of the optimal KL-constrained RL solution. We demonstrate that any alignment method that achieves a comparable trade-off between KL divergence and reward must approximate the optimal KL-constrained RL solution in terms of relative entropy. To further analyze the properties of alignment methods, we introduce two simplifying assumptions: we let the language model be memoryless, and the reward model be linear. Although these assumptions may not reflect complex real-world scenarios, they enable a precise characterization of the asymptotic behavior of both the best-of-$N$ alignment, and the KL-constrained RL method, in terms of information-theoretic quantities. We prove that the reward of the optimal KL-constrained RL solution satisfies a large deviation principle, and we fully characterize its rate function. We also show that the rate of growth of the scaled cumulants of the reward is characterized by a proper Renyi cross entropy. Finally, we show that best-of-$N$ is asymptotically equivalent to KL-constrained RL solution by proving that their expected rewards are asymptotically equal, and concluding that the two distributions must be close in KL divergence.

Optimal Block-Level Draft Verification for Accelerating Speculative Decoding

Speculative decoding has shown to be an effective method for lossless acceleration of large language models (LLMs) during inference. In each iteration, the algorithm first uses a smaller model to draft a block of tokens. The tokens are then verified by the large model in parallel and only a subset of tokens will be kept to guarantee that the final output follows the distribution of the large model. In all of the prior speculative decoding works, the draft verification is performed token-by-token independently. In this work, we propose a better draft verification algorithm that provides additional wall-clock speedup without incurring additional computation cost and draft tokens. We first formulate the draft verification step as a block-level optimal transport problem. The block-level formulation allows us to consider a wider range of draft verification algorithms and obtain a higher number of accepted tokens in expectation in one draft block. We propose a verification algorithm that achieves the optimal accepted length for the block-level transport problem. We empirically evaluate our proposed block-level verification algorithm in a wide range of tasks and datasets, and observe consistent improvements in wall-clock speedup when compared to token-level verification algorithm. To the best of our knowledge, our work is the first to establish improvement over speculative decoding through a better draft verification algorithm.

Efficient Language Model Architectures for Differentially Private Federated Learning

Cross-device federated learning (FL) is a technique that trains a model on data distributed across typically millions of edge devices without data leaving the devices. SGD is the standard client optimizer for on device training in cross-device FL, favored for its memory and computational efficiency. However, in centralized training of neural language models, adaptive optimizers are preferred as they offer improved stability and performance. In light of this, we ask if language models can be modified such that they can be efficiently trained with SGD client optimizers and answer this affirmatively. We propose a scale-invariant Coupled Input Forget Gate (SI CIFG) recurrent network by modifying the sigmoid and tanh activations in the recurrent cell and show that this new model converges faster and achieves better utility than the standard CIFG recurrent model in cross-device FL in large scale experiments. We further show that the proposed scale invariant modification also helps in federated learning of larger transformer models. Finally, we demonstrate the scale invariant modification is also compatible with other non-adaptive algorithms. Particularly, our results suggest an improved privacy utility trade-off in federated learning with differential privacy.

Theoretical guarantees on the best-of-n alignment policy

A simple and effective method for the alignment of generative models is the best-of-$n$ policy, where $n$ samples are drawn from a base policy, and ranked based on a reward function, and the highest ranking one is selected. A commonly used analytical expression in the literature claims that the KL divergence between the best-of-$n$ policy and the base policy is equal to $\log (n) - (n-1)/n.$ We disprove the validity of this claim, and show that it is an upper bound on the actual KL divergence. We also explore the tightness of this upper bound in different regimes. Finally, we propose a new estimator for the KL divergence and empirically show that it provides a tight approximation through a few examples.

Mean estimation in the add-remove model of differential privacy

Differential privacy is often studied under two different models of neighboring datasets: the add-remove model and the swap model. While the swap model is used extensively in the academic literature, many practical libraries use the more conservative add-remove model. However, analysis under the add-remove model can be cumbersome, and obtaining results with tight constants requires some additional work. Here, we study the problem of one-dimensional mean estimation under the add-remove model of differential privacy. We propose a new algorithm and show that it is min-max optimal, that it has the correct constant in the leading term of the mean squared error, and that this constant is the same as the optimal algorithm in the swap model. Our results show that, for mean estimation, the add-remove and swap model give nearly identical error even though the add-remove model cannot treat the size of the dataset as public information. In addition, we demonstrate empirically that our proposed algorithm yields a factor of two improvement in mean squared error over algorithms often used in practice.

Multi-Group Fairness Evaluation via Conditional Value-at-Risk Testing

Machine learning (ML) models used in prediction and classification tasks may display performance disparities across population groups determined by sensitive attributes (e.g., race, sex, age). We consider the problem of evaluating the performance of a fixed ML model across population groups defined by multiple sensitive attributes (e.g., race and sex and age). Here, the sample complexity for estimating the worst-case performance gap across groups (e.g., the largest difference in error rates) increases exponentially with the number of group-denoting sensitive attributes. To address this issue, we propose an approach to test for performance disparities based on Conditional Value-at-Risk (CVaR). By allowing a small probabilistic slack on the groups over which a model has approximately equal performance, we show that the sample complexity required for discovering performance violations is reduced exponentially to be at most upper bounded by the square root of the number of groups. As a byproduct of our analysis, when the groups are weighted by a specific prior distribution, we show that R\'enyi entropy of order $2/3$ of the prior distribution captures the sample complexity of the proposed CVaR test algorithm. Finally, we also show that there exists a non-i.i.d. data collection strategy that results in a sample complexity independent of the number of groups.