Asymptotics of Language Model Alignment
Paper and Code
Apr 02, 2024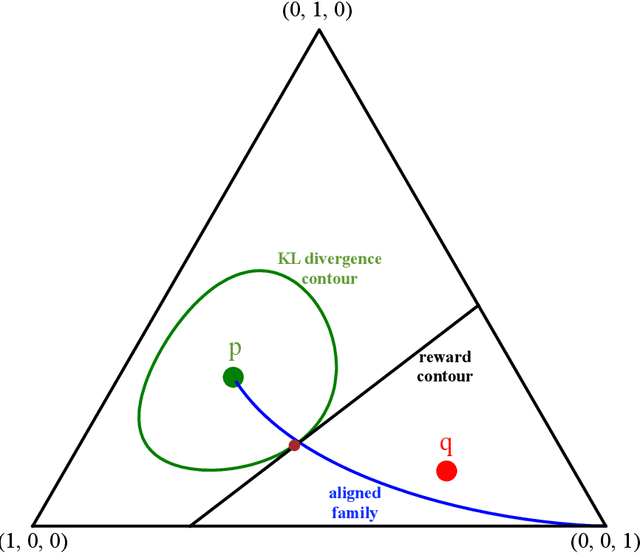
Let $p$ denote a generative language model. Let $r$ denote a reward model that returns a scalar that captures the degree at which a draw from $p$ is preferred. The goal of language model alignment is to alter $p$ to a new distribution $\phi$ that results in a higher expected reward while keeping $\phi$ close to $p.$ A popular alignment method is the KL-constrained reinforcement learning (RL), which chooses a distribution $\phi_\Delta$ that maximizes $E_{\phi_{\Delta}} r(y)$ subject to a relative entropy constraint $KL(\phi_\Delta || p) \leq \Delta.$ Another simple alignment method is best-of-$N$, where $N$ samples are drawn from $p$ and one with highest reward is selected. In this paper, we offer a closed-form characterization of the optimal KL-constrained RL solution. We demonstrate that any alignment method that achieves a comparable trade-off between KL divergence and reward must approximate the optimal KL-constrained RL solution in terms of relative entropy. To further analyze the properties of alignment methods, we introduce two simplifying assumptions: we let the language model be memoryless, and the reward model be linear. Although these assumptions may not reflect complex real-world scenarios, they enable a precise characterization of the asymptotic behavior of both the best-of-$N$ alignment, and the KL-constrained RL method, in terms of information-theoretic quantities. We prove that the reward of the optimal KL-constrained RL solution satisfies a large deviation principle, and we fully characterize its rate function. We also show that the rate of growth of the scaled cumulants of the reward is characterized by a proper Renyi cross entropy. Finally, we show that best-of-$N$ is asymptotically equivalent to KL-constrained RL solution by proving that their expected rewards are asymptotically equal, and concluding that the two distributions must be close in KL divergence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge