Salman Salamatian
Asymptotics of Language Model Alignment
Apr 02, 2024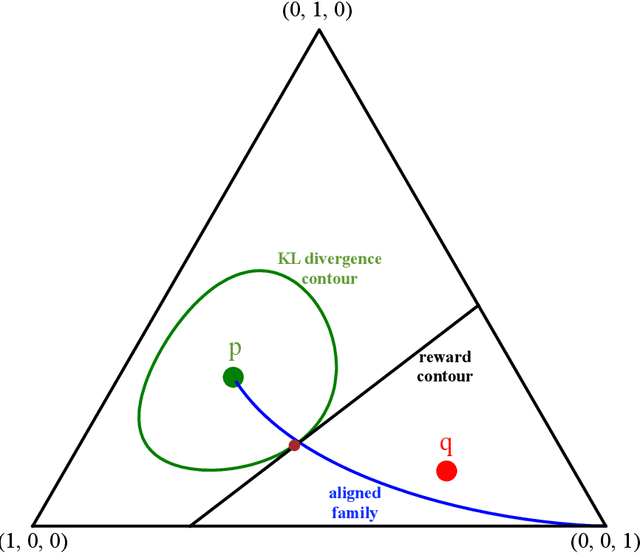
Abstract:Let $p$ denote a generative language model. Let $r$ denote a reward model that returns a scalar that captures the degree at which a draw from $p$ is preferred. The goal of language model alignment is to alter $p$ to a new distribution $\phi$ that results in a higher expected reward while keeping $\phi$ close to $p.$ A popular alignment method is the KL-constrained reinforcement learning (RL), which chooses a distribution $\phi_\Delta$ that maximizes $E_{\phi_{\Delta}} r(y)$ subject to a relative entropy constraint $KL(\phi_\Delta || p) \leq \Delta.$ Another simple alignment method is best-of-$N$, where $N$ samples are drawn from $p$ and one with highest reward is selected. In this paper, we offer a closed-form characterization of the optimal KL-constrained RL solution. We demonstrate that any alignment method that achieves a comparable trade-off between KL divergence and reward must approximate the optimal KL-constrained RL solution in terms of relative entropy. To further analyze the properties of alignment methods, we introduce two simplifying assumptions: we let the language model be memoryless, and the reward model be linear. Although these assumptions may not reflect complex real-world scenarios, they enable a precise characterization of the asymptotic behavior of both the best-of-$N$ alignment, and the KL-constrained RL method, in terms of information-theoretic quantities. We prove that the reward of the optimal KL-constrained RL solution satisfies a large deviation principle, and we fully characterize its rate function. We also show that the rate of growth of the scaled cumulants of the reward is characterized by a proper Renyi cross entropy. Finally, we show that best-of-$N$ is asymptotically equivalent to KL-constrained RL solution by proving that their expected rewards are asymptotically equal, and concluding that the two distributions must be close in KL divergence.
Wideband Time Frequency Coding
May 31, 2022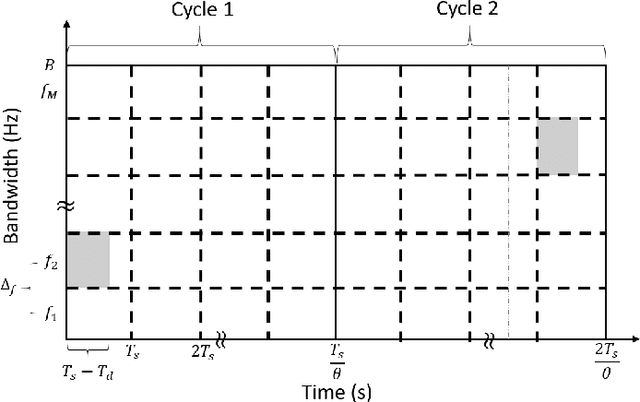
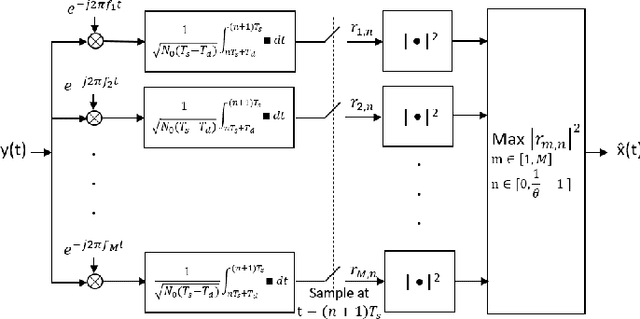
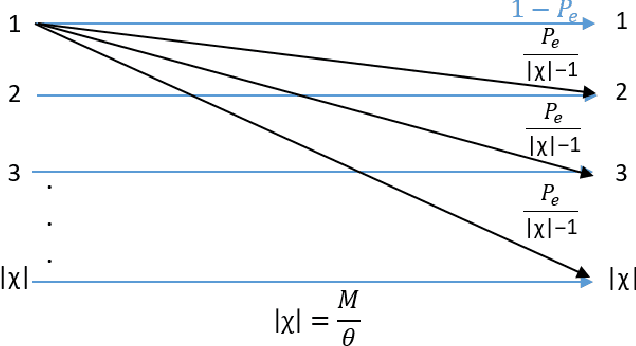
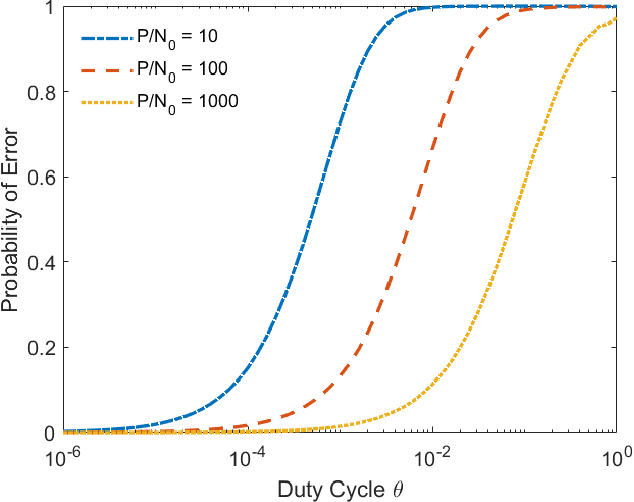
Abstract:In the wideband regime, the performance of many of the popular modulation schemes such as code division multiple access and orthogonal frequency division multiplexing falls quickly without channel state information. Obtaining the amount of channel information required for these techniques to work is costly and difficult, which suggests the need for schemes which can perform well without channel state information. In this work, we present one such scheme, called wideband time frequency coding, which achieves rates on the order of the additive white Gaussian noise capacity without requiring any channel state information. Wideband time frequency coding combines impulsive frequency shift keying with pulse position modulation, which allows for information to be encoded in both the transmitted frequency and the transmission time period. On the detection side, we propose a non-coherent decoder based on a square-law detector, akin to the optimal decoder for frequency shift keying based signals. The impacts of various parameters on the symbol error probability and capacity of wideband time frequency coding are investigated, and the results show that it is robust to shadowing and highly fading channels. When compared to other modulation schemes such as code division multiple access, orthogonal frequency division multiplexing, pulse position modulation, and impulsive frequency shift keying without channel state information, wideband time frequency coding achieves higher rates in the wideband regime, and performs comparably in smaller bandwidths.
Correspondence Analysis Using Neural Networks
Feb 21, 2019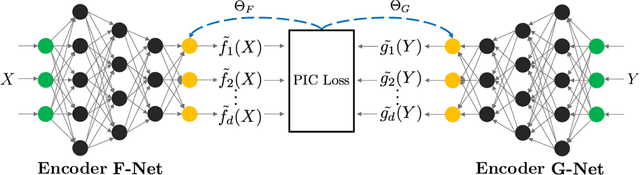

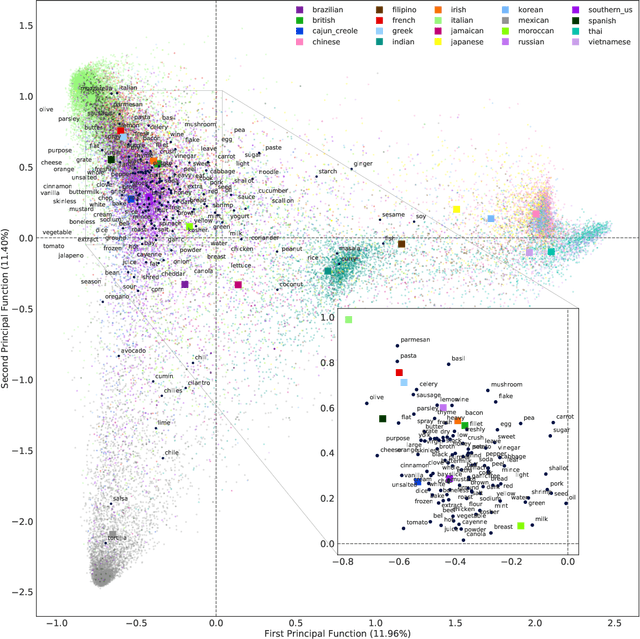
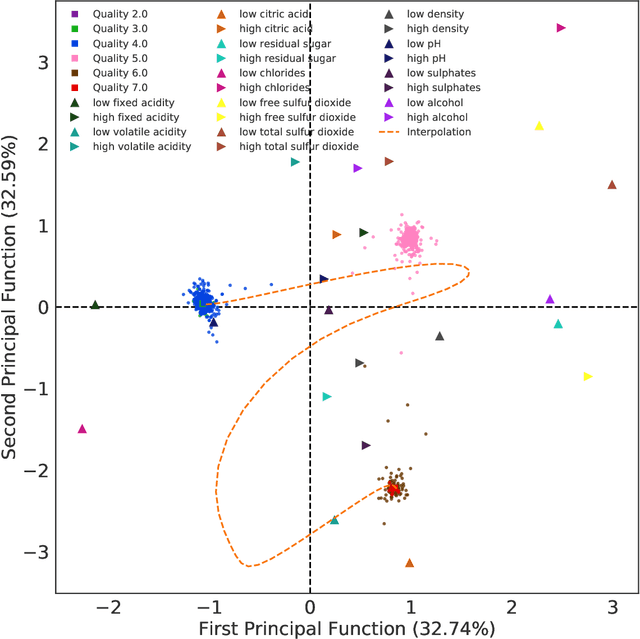
Abstract:Correspondence analysis (CA) is a multivariate statistical tool used to visualize and interpret data dependencies. CA has found applications in fields ranging from epidemiology to social sciences. However, current methods used to perform CA do not scale to large, high-dimensional datasets. By re-interpreting the objective in CA using an information-theoretic tool called the principal inertia components, we demonstrate that performing CA is equivalent to solving a functional optimization problem over the space of finite variance functions of two random variable. We show that this optimization problem, in turn, can be efficiently approximated by neural networks. The resulting formulation, called the correspondence analysis neural network (CA-NN), enables CA to be performed at an unprecedented scale. We validate the CA-NN on synthetic data, and demonstrate how it can be used to perform CA on a variety of datasets, including food recipes, wine compositions, and images. Our results outperform traditional methods used in CA, indicating that CA-NN can serve as a new, scalable tool for interpretability and visualization of complex dependencies between random variables.
Correspondence Analysis of Government Expenditure Patterns
Nov 29, 2018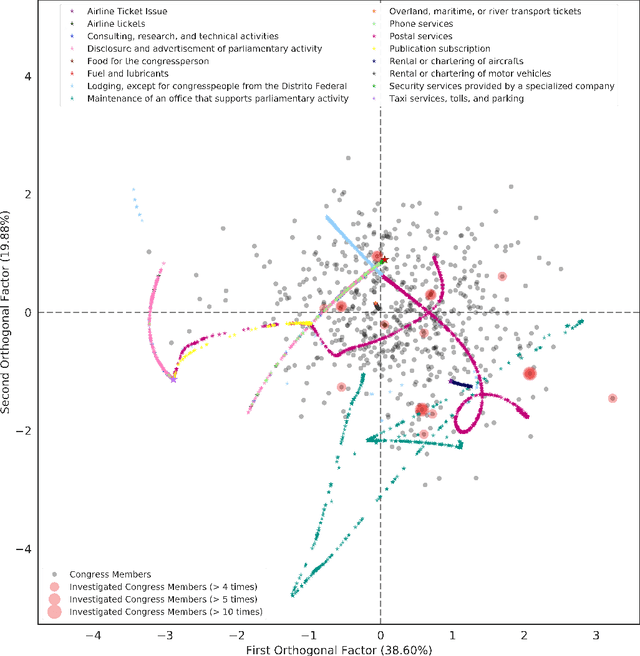
Abstract:We analyze expenditure patterns of discretionary funds by Brazilian congress members. This analysis is based on a large dataset containing over $7$ million expenses made publicly available by the Brazilian government. This dataset has, up to now, remained widely untouched by machine learning methods. Our main contributions are two-fold: (i) we provide a novel dataset benchmark for machine learning-based efforts for government transparency to the broader research community, and (ii) introduce a neural network-based approach for analyzing and visualizing outlying expense patterns. Our hope is that the approach presented here can inspire new machine learning methodologies for government transparency applicable to other developing nations.
Deep Orthogonal Representations: Fundamental Properties and Applications
Jun 21, 2018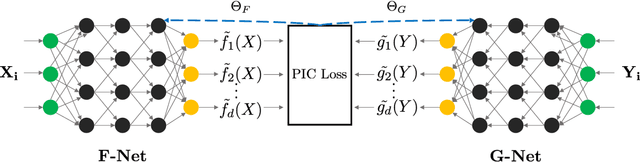
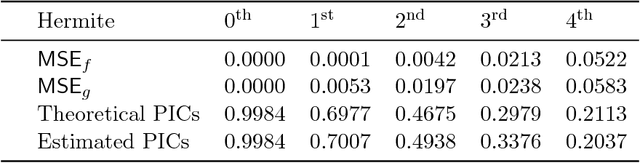
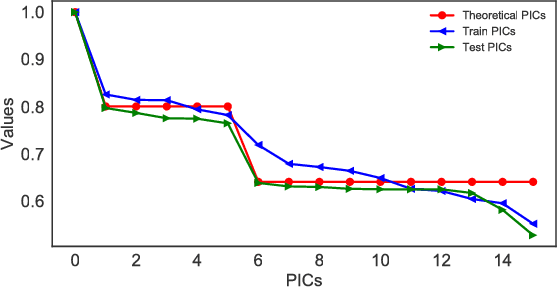

Abstract:Several representation learning and, more broadly, dimensionality reduction techniques seek to produce representations of the data that are orthogonal (uncorrelated). Examples include PCA, CCA, Kernel/Deep CCA, the ACE algorithm and correspondence analysis (CA). For a fixed data distribution, all finite variance representations belong to the same function space regardless of how they are derived. In this work, we present a theoretical framework for analyzing this function space, and demonstrate how a basis for this space can be found using neural networks. We show that this framework (i) underlies recent multi-view representation learning methods, (ii) enables classical exploratory statistical techniques such as CA to be scaled via neural networks, and (iii) can be used to derive new methods for comparing black-box models. We illustrate these applications empirically through different datasets.
Generalizing Bottleneck Problems
May 10, 2018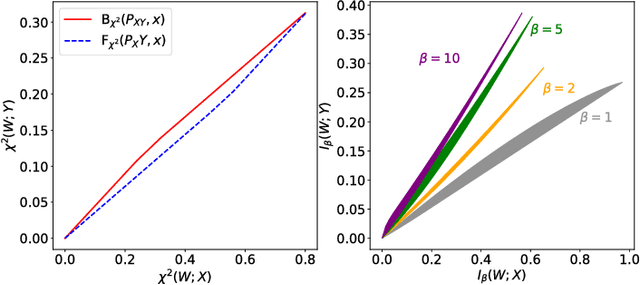
Abstract:Given a pair of random variables $(X,Y)\sim P_{XY}$ and two convex functions $f_1$ and $f_2$, we introduce two bottleneck functionals as the lower and upper boundaries of the two-dimensional convex set that consists of the pairs $\left(I_{f_1}(W; X), I_{f_2}(W; Y)\right)$, where $I_f$ denotes $f$-information and $W$ varies over the set of all discrete random variables satisfying the Markov condition $W \to X \to Y$. Applying Witsenhausen and Wyner's approach, we provide an algorithm for computing boundaries of this set for $f_1$, $f_2$, and discrete $P_{XY}$. In the binary symmetric case, we fully characterize the set when (i) $f_1(t)=f_2(t)=t\log t$, (ii) $f_1(t)=f_2(t)=t^2-1$, and (iii) $f_1$ and $f_2$ are both $\ell^\beta$ norm function for $\beta \geq 2$. We then argue that upper and lower boundaries in (i) correspond to Mrs. Gerber's Lemma and its inverse (which we call Mr. Gerber's Lemma), in (ii) correspond to estimation-theoretic variants of Information Bottleneck and Privacy Funnel, and in (iii) correspond to Arimoto Information Bottleneck and Privacy Funnel.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge