Deep Orthogonal Representations: Fundamental Properties and Applications

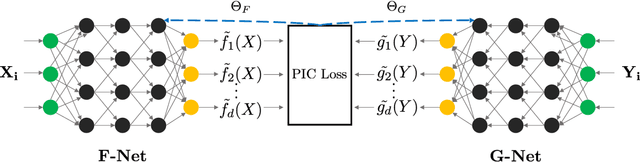
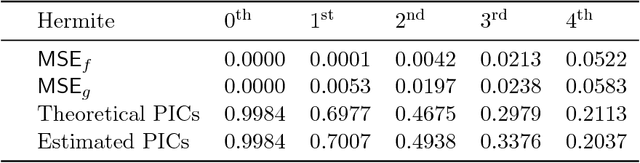
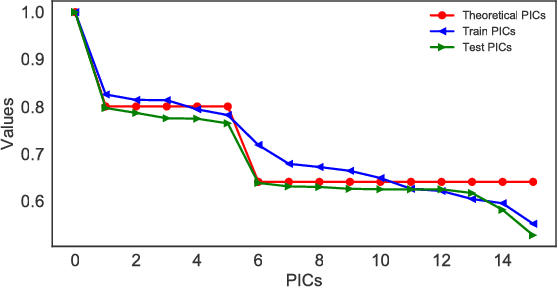
Several representation learning and, more broadly, dimensionality reduction techniques seek to produce representations of the data that are orthogonal (uncorrelated). Examples include PCA, CCA, Kernel/Deep CCA, the ACE algorithm and correspondence analysis (CA). For a fixed data distribution, all finite variance representations belong to the same function space regardless of how they are derived. In this work, we present a theoretical framework for analyzing this function space, and demonstrate how a basis for this space can be found using neural networks. We show that this framework (i) underlies recent multi-view representation learning methods, (ii) enables classical exploratory statistical techniques such as CA to be scaled via neural networks, and (iii) can be used to derive new methods for comparing black-box models. We illustrate these applications empirically through different datasets.