Entropy Equivalence Testing

We introduce the problem of \emph{entropy equivalence testing} for probability distributions, a relaxation of the well-studied closeness testing problem, where the distribution testing algorithm is now only required to distinguish, given samples from two unknown distributions $p,q$ and a parameter $\varepsilon \in(0,1/2]$, between $p=q$ and $|H(p)-H(q)| \geq \varepsilon$ (where $H$ denotes the Shannon entropy). We provide a time- and sample-efficient algorithm for this task, showing that the optimal sample complexity for this task can be significantly lower than that of closeness testing. As an application, we leverage this result to provide the first non-trivial testing algorithm for (standard) closeness of low-degree \emph{Bayesian networks}, which significantly improves on either the sample or time complexity of a baseline based on full learning.

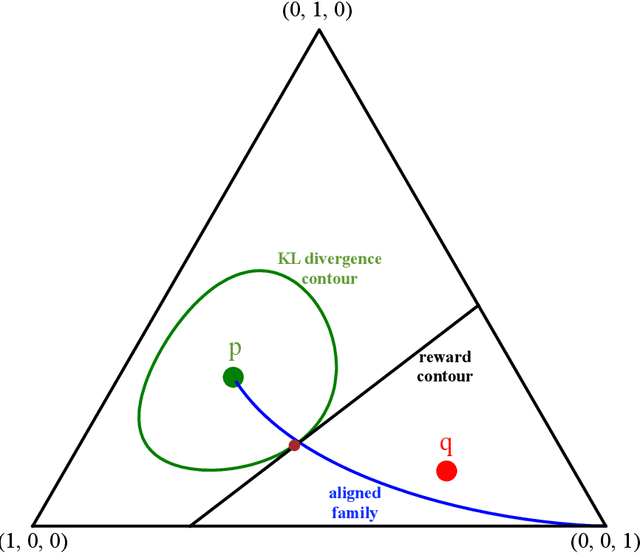
Asymptotics of Language Model Alignment

Let $p$ denote a generative language model. Let $r$ denote a reward model that returns a scalar that captures the degree at which a draw from $p$ is preferred. The goal of language model alignment is to alter $p$ to a new distribution $\phi$ that results in a higher expected reward while keeping $\phi$ close to $p.$ A popular alignment method is the KL-constrained reinforcement learning (RL), which chooses a distribution $\phi_\Delta$ that maximizes $E_{\phi_{\Delta}} r(y)$ subject to a relative entropy constraint $KL(\phi_\Delta || p) \leq \Delta.$ Another simple alignment method is best-of-$N$, where $N$ samples are drawn from $p$ and one with highest reward is selected. In this paper, we offer a closed-form characterization of the optimal KL-constrained RL solution. We demonstrate that any alignment method that achieves a comparable trade-off between KL divergence and reward must approximate the optimal KL-constrained RL solution in terms of relative entropy. To further analyze the properties of alignment methods, we introduce two simplifying assumptions: we let the language model be memoryless, and the reward model be linear. Although these assumptions may not reflect complex real-world scenarios, they enable a precise characterization of the asymptotic behavior of both the best-of-$N$ alignment, and the KL-constrained RL method, in terms of information-theoretic quantities. We prove that the reward of the optimal KL-constrained RL solution satisfies a large deviation principle, and we fully characterize its rate function. We also show that the rate of growth of the scaled cumulants of the reward is characterized by a proper Renyi cross entropy. Finally, we show that best-of-$N$ is asymptotically equivalent to KL-constrained RL solution by proving that their expected rewards are asymptotically equal, and concluding that the two distributions must be close in KL divergence.

Learning bounded-degree polytrees with known skeleton

We establish finite-sample guarantees for efficient proper learning of bounded-degree polytrees, a rich class of high-dimensional probability distributions and a subclass of Bayesian networks, a widely-studied type of graphical model. Recently, Bhattacharyya et al. (2021) obtained finite-sample guarantees for recovering tree-structured Bayesian networks, i.e., 1-polytrees. We extend their results by providing an efficient algorithm which learns $d$-polytrees in polynomial time and sample complexity for any bounded $d$ when the underlying undirected graph (skeleton) is known. We complement our algorithm with an information-theoretic sample complexity lower bound, showing that the dependence on the dimension and target accuracy parameters are nearly tight.

Near-Optimal Degree Testing for Bayes Nets

This paper considers the problem of testing the maximum in-degree of the Bayes net underlying an unknown probability distribution $P$ over $\{0,1\}^n$, given sample access to $P$. We show that the sample complexity of the problem is $\tilde{\Theta}(2^{n/2}/\varepsilon^2)$. Our algorithm relies on a testing-by-learning framework, previously used to obtain sample-optimal testers; in order to apply this framework, we develop new algorithms for ``near-proper'' learning of Bayes nets, and high-probability learning under $\chi^2$ divergence, which are of independent interest.

Independence Testing for Bounded Degree Bayesian Network

We study the following independence testing problem: given access to samples from a distribution $P$ over $\{0,1\}^n$, decide whether $P$ is a product distribution or whether it is $\varepsilon$-far in total variation distance from any product distribution. For arbitrary distributions, this problem requires $\exp(n)$ samples. We show in this work that if $P$ has a sparse structure, then in fact only linearly many samples are required. Specifically, if $P$ is Markov with respect to a Bayesian network whose underlying DAG has in-degree bounded by $d$, then $\tilde{\Theta}(2^{d/2}\cdot n/\varepsilon^2)$ samples are necessary and sufficient for independence testing.