Multi-Mixer Models: Flexible Sequence Modeling with Shared Representations

Softmax attention is the cornerstone of modern large language models, but its memory scales linearly and compute quadratically with sequence length. Linear recurrent models, such as linear attention and state space models, have become widely studied as alternatives to attention due to their linear compute and constant memory. While these sub-quadratic token mixing methods, or mixers, achieve promising efficiency gains and competitive results on a wide range of benchmarks, current linear recurrent models still lag behind on tasks that require long-context retrieval or in-context learning. A growing body of work studies hybrid architectures that attempt to mitigate these trade-offs by statically interleaving or merging attention and recurrent blocks. In this work, we explore a new axis of developing hybrid models: across the token sequence. We propose Oryx, a hybrid model that can, throughout a sequence, flexibly switch between different mixers, for example quadratic attention for rich context utilization and linear recurrences for efficient generation. Oryx ties at least 90% of its parameters across mixers, enabling attention and recurrent modes to operate over shared internal representations. We validate our design with Mamba-2 and Gated DeltaNet variants, up to 1.4B models. Under fixed token budgets and a mixed-training strategy, Oryx achieves comparable or better performance than its single-mixer baselines. At the 1.4B scale, all instances of Oryx outperform their respective baselines by at least 0.7 percentage points on averaged language modeling tasks. On retrieval tasks, Oryx achieves performance comparable to the Transformer baseline even when processing only a tiny fraction (<10%) of the tokens in attention mode. These results suggest that attention and linear recurrent models can share internal representations, and motivate sequence-axis hybridization as a promising direction.

InfAlign: Inference-aware language model alignment

Language model alignment has become a critical step in training modern generative language models. The goal of alignment is to finetune a reference model such that the win rate of a sample from the aligned model over a sample from the reference model is high, subject to a KL divergence constraint. Today, we are increasingly using inference-time algorithms (e.g., Best-of-N, controlled decoding, tree search) to decode from language models rather than standard sampling. However, the alignment objective does not capture such inference-time decoding procedures. We show that the existing alignment framework is sub-optimal in view of such inference-time methods. We then modify the alignment objective and propose a framework for inference-aware alignment (IAPO). We prove that for any inference-time decoding algorithm, the optimal solution that optimizes the inference-time win rate of the aligned policy against the reference policy is the solution to the typical RLHF problem with a transformation of the reward. This motivates us to provide the KL-regularized calibrate-and-transform RL (CTRL) algorithm to solve this problem, which involves a reward calibration step and a KL-regularized reward maximization step with a transformation of the calibrated reward. We particularize our study to two important inference-time strategies: best-of-N sampling and best-of-N jailbreaking, where N responses are sampled from the model and the one with the highest or lowest reward is selected. We propose specific transformations for these strategies and demonstrate that our framework offers significant improvements over existing state-of-the-art methods for language model alignment. Empirically, we outperform baselines that are designed without taking inference-time decoding into consideration by 8-12% and 4-9% on inference-time win rates over the Anthropic helpfulness and harmlessness dialog benchmark datasets.

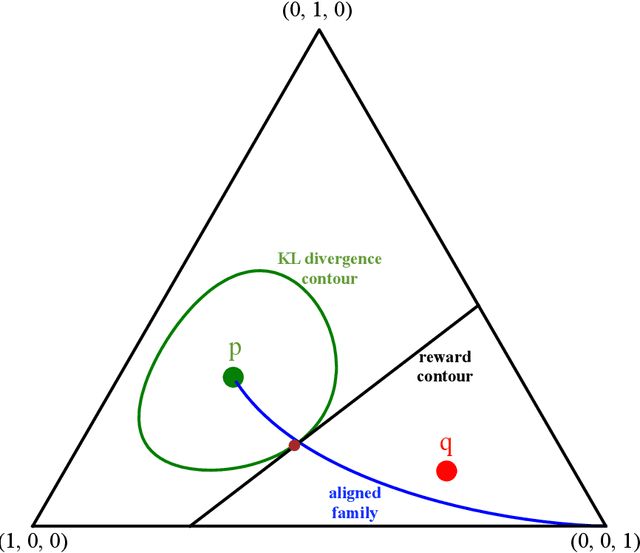
Asymptotics of Language Model Alignment

Let $p$ denote a generative language model. Let $r$ denote a reward model that returns a scalar that captures the degree at which a draw from $p$ is preferred. The goal of language model alignment is to alter $p$ to a new distribution $\phi$ that results in a higher expected reward while keeping $\phi$ close to $p.$ A popular alignment method is the KL-constrained reinforcement learning (RL), which chooses a distribution $\phi_\Delta$ that maximizes $E_{\phi_{\Delta}} r(y)$ subject to a relative entropy constraint $KL(\phi_\Delta || p) \leq \Delta.$ Another simple alignment method is best-of-$N$, where $N$ samples are drawn from $p$ and one with highest reward is selected. In this paper, we offer a closed-form characterization of the optimal KL-constrained RL solution. We demonstrate that any alignment method that achieves a comparable trade-off between KL divergence and reward must approximate the optimal KL-constrained RL solution in terms of relative entropy. To further analyze the properties of alignment methods, we introduce two simplifying assumptions: we let the language model be memoryless, and the reward model be linear. Although these assumptions may not reflect complex real-world scenarios, they enable a precise characterization of the asymptotic behavior of both the best-of-$N$ alignment, and the KL-constrained RL method, in terms of information-theoretic quantities. We prove that the reward of the optimal KL-constrained RL solution satisfies a large deviation principle, and we fully characterize its rate function. We also show that the rate of growth of the scaled cumulants of the reward is characterized by a proper Renyi cross entropy. Finally, we show that best-of-$N$ is asymptotically equivalent to KL-constrained RL solution by proving that their expected rewards are asymptotically equal, and concluding that the two distributions must be close in KL divergence.

Optimal Block-Level Draft Verification for Accelerating Speculative Decoding

Speculative decoding has shown to be an effective method for lossless acceleration of large language models (LLMs) during inference. In each iteration, the algorithm first uses a smaller model to draft a block of tokens. The tokens are then verified by the large model in parallel and only a subset of tokens will be kept to guarantee that the final output follows the distribution of the large model. In all of the prior speculative decoding works, the draft verification is performed token-by-token independently. In this work, we propose a better draft verification algorithm that provides additional wall-clock speedup without incurring additional computation cost and draft tokens. We first formulate the draft verification step as a block-level optimal transport problem. The block-level formulation allows us to consider a wider range of draft verification algorithms and obtain a higher number of accepted tokens in expectation in one draft block. We propose a verification algorithm that achieves the optimal accepted length for the block-level transport problem. We empirically evaluate our proposed block-level verification algorithm in a wide range of tasks and datasets, and observe consistent improvements in wall-clock speedup when compared to token-level verification algorithm. To the best of our knowledge, our work is the first to establish improvement over speculative decoding through a better draft verification algorithm.

SpecTr: Fast Speculative Decoding via Optimal Transport

Autoregressive sampling from large language models has led to state-of-the-art results in several natural language tasks. However, autoregressive sampling generates tokens one at a time making it slow, and even prohibitive in certain tasks. One way to speed up sampling is $\textit{speculative decoding}$: use a small model to sample a $\textit{draft}$ (block or sequence of tokens), and then score all tokens in the draft by the large language model in parallel. A subset of the tokens in the draft are accepted (and the rest rejected) based on a statistical method to guarantee that the final output follows the distribution of the large model. In this work, we provide a principled understanding of speculative decoding through the lens of optimal transport (OT) with $\textit{membership cost}$. This framework can be viewed as an extension of the well-known $\textit{maximal-coupling}$ problem. This new formulation enables us to generalize the speculative decoding method to allow for a set of $k$ candidates at the token-level, which leads to an improved optimal membership cost. We show that the optimal draft selection algorithm (transport plan) can be computed via linear programming, whose best-known runtime is exponential in $k$. We then propose a valid draft selection algorithm whose acceptance probability is $(1-1/e)$-optimal multiplicatively. Moreover, it can be computed in time almost linear with size of domain of a single token. Using this $new draft selection$ algorithm, we develop a new autoregressive sampling algorithm called $\textit{SpecTr}$, which provides speedup in decoding while ensuring that there is no quality degradation in the decoded output. We experimentally demonstrate that for state-of-the-art large language models, the proposed approach achieves a wall clock speedup of 2.13X, a further 1.37X speedup over speculative decoding on standard benchmarks.

The importance of feature preprocessing for differentially private linear optimization

Training machine learning models with differential privacy (DP) has received increasing interest in recent years. One of the most popular algorithms for training differentially private models is differentially private stochastic gradient descent (DPSGD) and its variants, where at each step gradients are clipped and combined with some noise. Given the increasing usage of DPSGD, we ask the question: is DPSGD alone sufficient to find a good minimizer for every dataset under privacy constraints? As a first step towards answering this question, we show that even for the simple case of linear classification, unlike non-private optimization, (private) feature preprocessing is vital for differentially private optimization. In detail, we first show theoretically that there exists an example where without feature preprocessing, DPSGD incurs a privacy error proportional to the maximum norm of features over all samples. We then propose an algorithm called DPSGD-F, which combines DPSGD with feature preprocessing and prove that for classification tasks, it incurs a privacy error proportional to the diameter of the features $\max_{x, x' \in D} \|x - x'\|_2$. We then demonstrate the practicality of our algorithm on image classification benchmarks.

Subset-Based Instance Optimality in Private Estimation

We propose a new definition of instance optimality for differentially private estimation algorithms. Our definition requires an optimal algorithm to compete, simultaneously for every dataset $D$, with the best private benchmark algorithm that (a) knows $D$ in advance and (b) is evaluated by its worst-case performance on large subsets of $D$. That is, the benchmark algorithm need not perform well when potentially extreme points are added to $D$; it only has to handle the removal of a small number of real data points that already exist. This makes our benchmark significantly stronger than those proposed in prior work. We nevertheless show, for real-valued datasets, how to construct private algorithms that achieve our notion of instance optimality when estimating a broad class of dataset properties, including means, quantiles, and $\ell_p$-norm minimizers. For means in particular, we provide a detailed analysis and show that our algorithm simultaneously matches or exceeds the asymptotic performance of existing algorithms under a range of distributional assumptions.

Concentration Bounds for Discrete Distribution Estimation in KL Divergence

We study the problem of discrete distribution estimation in KL divergence and provide concentration bounds for the Laplace estimator. We show that the deviation from mean scales as $\sqrt{k}/n$ when $n \ge k$, improving upon the best prior result of $k/n$. We also establish a matching lower bound that shows that our bounds are tight up to polylogarithmic factors.

Discrete Distribution Estimation under User-level Local Differential Privacy

We study discrete distribution estimation under user-level local differential privacy (LDP). In user-level $\varepsilon$-LDP, each user has $m\ge1$ samples and the privacy of all $m$ samples must be preserved simultaneously. We resolve the following dilemma: While on the one hand having more samples per user should provide more information about the underlying distribution, on the other hand, guaranteeing the privacy of all $m$ samples should make the estimation task more difficult. We obtain tight bounds for this problem under almost all parameter regimes. Perhaps surprisingly, we show that in suitable parameter regimes, having $m$ samples per user is equivalent to having $m$ times more users, each with only one sample. Our results demonstrate interesting phase transitions for $m$ and the privacy parameter $\varepsilon$ in the estimation risk. Finally, connecting with recent results on shuffled DP, we show that combined with random shuffling, our algorithm leads to optimal error guarantees (up to logarithmic factors) under the central model of user-level DP in certain parameter regimes. We provide several simulations to verify our theoretical findings.

The Role of Interactivity in Structured Estimation

We study high-dimensional sparse estimation under three natural constraints: communication constraints, local privacy constraints, and linear measurements (compressive sensing). Without sparsity assumptions, it has been established that interactivity cannot improve the minimax rates of estimation under these information constraints. The question of whether interactivity helps with natural inference tasks has been a topic of active research. We settle this question in the affirmative for the prototypical problems of high-dimensional sparse mean estimation and compressive sensing, by demonstrating a gap between interactive and noninteractive protocols. We further establish that the gap increases when we have more structured sparsity: for block sparsity this gap can be as large as polynomial in the dimensionality. Thus, the more structured the sparsity is, the greater is the advantage of interaction. Proving the lower bounds requires a careful breaking of a sum of correlated random variables into independent components using Baranyai's theorem on decomposition of hypergraphs, which might be of independent interest.