OML: Open, Monetizable, and Loyal AI

Artificial Intelligence (AI) has steadily improved across a wide range of tasks. However, the development and deployment of AI are almost entirely controlled by a few powerful organizations that are racing to create Artificial General Intelligence (AGI). The centralized entities make decisions with little public oversight, shaping the future of humanity, often with unforeseen consequences. In this paper, we propose OML, which stands for Open, Monetizable, and Loyal AI, an approach designed to democratize AI development. OML is realized through an interdisciplinary framework spanning AI, blockchain, and cryptography. We present several ideas for constructing OML using technologies such as Trusted Execution Environments (TEE), traditional cryptographic primitives like fully homomorphic encryption and functional encryption, obfuscation, and AI-native solutions rooted in the sample complexity and intrinsic hardness of AI tasks. A key innovation of our work is introducing a new scientific field: AI-native cryptography. Unlike conventional cryptography, which focuses on discrete data and binary security guarantees, AI-native cryptography exploits the continuous nature of AI data representations and their low-dimensional manifolds, focusing on improving approximate performance. One core idea is to transform AI attack methods, such as data poisoning, into security tools. This novel approach serves as a foundation for OML 1.0 which uses model fingerprinting to protect the integrity and ownership of AI models. The spirit of OML is to establish a decentralized, open, and transparent platform for AI development, enabling the community to contribute, monetize, and take ownership of AI models. By decentralizing control and ensuring transparency through blockchain technology, OML prevents the concentration of power and provides accountability in AI development that has not been possible before.

Continual Mean Estimation Under User-Level Privacy

We consider the problem of continually releasing an estimate of the population mean of a stream of samples that is user-level differentially private (DP). At each time instant, a user contributes a sample, and the users can arrive in arbitrary order. Until now these requirements of continual release and user-level privacy were considered in isolation. But, in practice, both these requirements come together as the users often contribute data repeatedly and multiple queries are made. We provide an algorithm that outputs a mean estimate at every time instant $t$ such that the overall release is user-level $\varepsilon$-DP and has the following error guarantee: Denoting by $M_t$ the maximum number of samples contributed by a user, as long as $\tilde{\Omega}(1/\varepsilon)$ users have $M_t/2$ samples each, the error at time $t$ is $\tilde{O}(1/\sqrt{t}+\sqrt{M}_t/t\varepsilon)$. This is a universal error guarantee which is valid for all arrival patterns of the users. Furthermore, it (almost) matches the existing lower bounds for the single-release setting at all time instants when users have contributed equal number of samples.

The Role of Interactivity in Structured Estimation

We study high-dimensional sparse estimation under three natural constraints: communication constraints, local privacy constraints, and linear measurements (compressive sensing). Without sparsity assumptions, it has been established that interactivity cannot improve the minimax rates of estimation under these information constraints. The question of whether interactivity helps with natural inference tasks has been a topic of active research. We settle this question in the affirmative for the prototypical problems of high-dimensional sparse mean estimation and compressive sensing, by demonstrating a gap between interactive and noninteractive protocols. We further establish that the gap increases when we have more structured sparsity: for block sparsity this gap can be as large as polynomial in the dimensionality. Thus, the more structured the sparsity is, the greater is the advantage of interaction. Proving the lower bounds requires a careful breaking of a sum of correlated random variables into independent components using Baranyai's theorem on decomposition of hypergraphs, which might be of independent interest.

Fundamental limits of over-the-air optimization: Are analog schemes optimal?

We consider over-the-air convex optimization on a $d-$dimensional space where coded gradients are sent over an additive Gaussian noise channel with variance $\sigma^2$. The codewords satisfy an average power constraint $P$, resulting in the signal-to-noise ratio (SNR) of $P/\sigma^2$. We derive bounds for the convergence rates for over-the-air optimization. Our first result is a lower bound for the convergence rate showing that any code must slowdown the convergence rate by a factor of roughly $\sqrt{d/\log(1+\mathtt{SNR})}$. Next, we consider a popular class of schemes called $analog$ $coding$, where a linear function of the gradient is sent. We show that a simple scaled transmission analog coding scheme results in a slowdown in convergence rate by a factor of $\sqrt{d(1+1/\mathtt{SNR})}$. This matches the previous lower bound up to constant factors for low SNR, making the scaled transmission scheme optimal at low SNR. However, we show that this slowdown is necessary for any analog coding scheme. In particular, a slowdown in convergence by a factor of $\sqrt{d}$ for analog coding remains even when SNR tends to infinity. Remarkably, we present a simple quantize-and-modulate scheme that uses $Amplitude$ $Shift$ $Keying$ and almost attains the optimal convergence rate at all SNRs.

Multiple Support Recovery Using Very Few Measurements Per Sample

In the problem of multiple support recovery, we are given access to linear measurements of multiple sparse samples in $\mathbb{R}^{d}$. These samples can be partitioned into $\ell$ groups, with samples having the same support belonging to the same group. For a given budget of $m$ measurements per sample, the goal is to recover the $\ell$ underlying supports, in the absence of the knowledge of group labels. We study this problem with a focus on the measurement-constrained regime where $m$ is smaller than the support size $k$ of each sample. We design a two-step procedure that estimates the union of the underlying supports first, and then uses a spectral algorithm to estimate the individual supports. Our proposed estimator can recover the supports with $m<k$ measurements per sample, from $\tilde{O}(k^{4}\ell^{4}/m^{4})$ samples. Our guarantees hold for a general, generative model assumption on the samples and measurement matrices. We also provide results from experiments conducted on synthetic data and on the MNIST dataset.

Wyner-Ziv Estimators: Efficient Distributed Mean Estimation with Side Information

Communication efficient distributed mean estimation is an important primitive that arises in many distributed learning and optimization scenarios such as federated learning. Without any probabilistic assumptions on the underlying data, we study the problem of distributed mean estimation where the server has access to side information. We propose \emph{Wyner-Ziv estimators}, which are communication and computationally efficient and near-optimal when an upper bound for the distance between the side information and the data is known. As a corollary, we also show that our algorithms provide efficient schemes for the classic Wyner-Ziv problem in information theory. In a different direction, when there is no knowledge assumed about the distance between side information and the data, we present an alternative Wyner-Ziv estimator that uses correlated sampling. This latter setting offers {\em universal recovery guarantees}, and perhaps will be of interest in practice when the number of users is large and keeping track of the distances between the data and the side information may not be possible.

General lower bounds for interactive high-dimensional estimation under information constraints

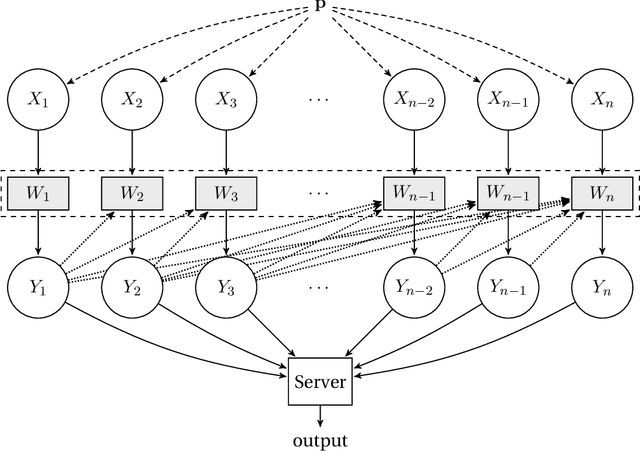
We consider the task of distributed parameter estimation using sequentially interactive protocols subject to local information constraints such as bandwidth limitations, local differential privacy, and restricted measurements. We provide a general framework enabling us to derive a variety of (tight) minimax lower bounds under different parametric families of distributions, both continuous and discrete, under any $\ell_p$ loss. Our lower bound framework is versatile, and yields "plug-and-play" bounds that are widely applicable to a large range of estimation problems. In particular, our approach recovers bounds obtained using data processing inequalities and Cram\'er-Rao bounds, two other alternative approaches for proving lower bounds in our setting of interest. Further, for the families considered, we complement our lower bounds with matching upper bounds.

Interactive Inference under Information Constraints

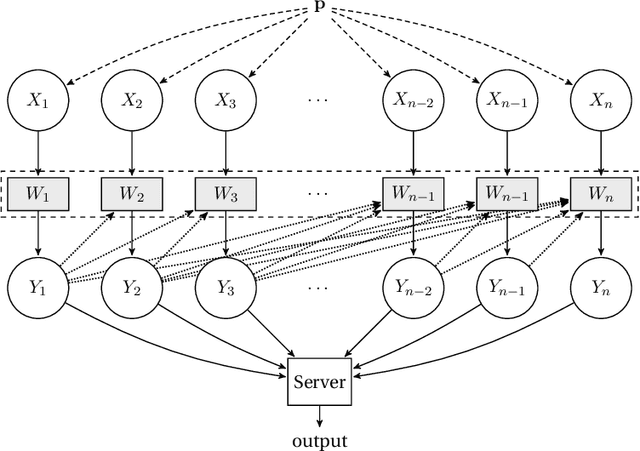
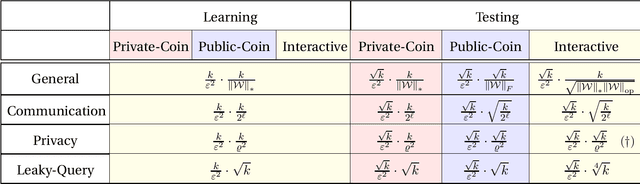
We consider distributed inference using sequentially interactive protocols. We obtain lower bounds on the minimax sample complexity of interactive protocols under local information constraints, a broad family of resource constraints which captures communication constraints, local differential privacy, and noisy binary queries as special cases. We focus on the inference tasks of learning (density estimation) and identity testing (goodness-of-fit) for discrete distributions under total variation distance, and establish general lower bounds that take into account the local constraints modeled as a channel family. Our main technical contribution is an approach to handle the correlation that builds due to interactivity and quantifies how effectively one can exploit this correlation in spite of the local constraints. Using this, we fill gaps in some prior works and characterize the optimal sample complexity of learning and testing discrete distributions under total variation distance, for both communication and local differential privacy constraints. Prior to our work, this was known only for the problem of testing under local privacy constraints (Amin, Joseph, and Mao (2020); Berrett and Butucea (2020)). Our results show that interactivity does not help for learning or testing under these two constraints. Finally, we provide the first instance of a natural family of "leaky query" local constraints under which interactive protocols strictly outperform the noninteractive ones for distribution testing.

How Reliable are Test Numbers for Revealing the COVID-19 Ground Truth and Applying Interventions?

The number of confirmed cases of COVID-19 is often used as a proxy for the actual number of ground truth COVID-19 infected cases in both public discourse and policy making. However, the number of confirmed cases depends on the testing policy, and it is important to understand how the number of positive cases obtained using different testing policies reveals the unknown ground truth. We develop an agent-based simulation framework in Python that can simulate various testing policies as well as interventions such as lockdown based on them. The interaction between the agents can take into account various communities and mobility patterns. A distinguishing feature of our framework is the presence of another `flu'-like illness with symptoms similar to COVID-19, that allows us to model the noise in selecting the pool of patients to be tested. We instantiate our model for the city of Bengaluru in India, using census data to distribute agents geographically, and traffic flow mobility data to model long-distance interactions and mixing. We use the simulation framework to compare the performance of three testing policies: Random Symptomatic Testing (RST), Contact Tracing (CT), and a new Location Based Testing policy (LBT). We observe that if a sufficient fraction of symptomatic patients come out for testing, then RST can capture the ground truth quite closely even with very few daily tests. However, CT consistently captures more positive cases. Interestingly, our new LBT, which is operationally less intensive than CT, gives performance that is comparable with CT. In another direction, we compare the efficacy of these three testing policies in enabling lockdown, and observe that CT flattens the ground truth curve maximally, followed closely by LBT, and significantly better than RST.

Finite Precision Stochastic Optimization -- Accounting for the Bias

We consider first order stochastic optimization where the oracle must quantize each subgradient estimate to $r$ bits. We treat two oracle models: the first where the Euclidean norm of the oracle output is almost surely bounded and the second where it is mean square bounded. Prior work in this setting assumes the availability of unbiased quantizers. While this assumption is valid in the case of almost surely bounded oracles, it does not hold true for the standard setting of mean square bounded oracles, and the bias can dramatically affect the convergence rate. We analyze the performance of standard quantizers from prior work in combination with projected stochastic gradient descent for both these oracle models and present two new adaptive quantizers that outperform the existing ones. Specifically, for almost surely bounded oracles, we establish first a lower bound for the precision needed to attain the standard convergence rate of $T^{-\frac 12}$ for optimizing convex functions over a $d$-dimentional domain. Our proposed Rotated Adaptive Tetra-iterated Quantizer (RATQ) is merely a factor $O(\log \log \log^\ast d)$ far from this lower bound. For mean square bounded oracles, we show that a state-of-the-art Rotated Uniform Quantizer (RUQ) from prior work would need atleast $\Omega(d\log T)$ bits to achieve the convergence rate of $T^{-\frac 12}$, using any optimization protocol. However, our proposed Rotated Adaptive Quantizer (RAQ) outperforms RUQ in this setting and attains a convergence rate of $T^{-\frac 12}$ using a precision of only $O(d\log\log T)$. For mean square bounded oracles, in the communication-starved regime where the precision $r$ is fixed to a constant independent of $T$, we show that RUQ cannot attain a convergence rate better than $T^{-\frac 14}$ for any $r$, while RAQ can attain convergence at rates arbitrarily close to $T^{-\frac 12}$ as $r$ increases.