Asymptotic Learning Curves for Diffusion Models with Random Features Score and Manifold Data

We study the theoretical behavior of denoising score matching--the learning task associated to diffusion models--when the data distribution is supported on a low-dimensional manifold and the score is parameterized using a random feature neural network. We derive asymptotically exact expressions for the test, train, and score errors in the high-dimensional limit. Our analysis reveals that, for linear manifolds the sample complexity required to learn the score function scales linearly with the intrinsic dimension of the manifold, rather than with the ambient dimension. Perhaps surprisingly, the benefits of low-dimensional structure starts to diminish once we have a non-linear manifold. These results indicate that diffusion models can benefit from structured data; however, the dependence on the specific type of structure is subtle and intricate.

Continual Mean Estimation Under User-Level Privacy

We consider the problem of continually releasing an estimate of the population mean of a stream of samples that is user-level differentially private (DP). At each time instant, a user contributes a sample, and the users can arrive in arbitrary order. Until now these requirements of continual release and user-level privacy were considered in isolation. But, in practice, both these requirements come together as the users often contribute data repeatedly and multiple queries are made. We provide an algorithm that outputs a mean estimate at every time instant $t$ such that the overall release is user-level $\varepsilon$-DP and has the following error guarantee: Denoting by $M_t$ the maximum number of samples contributed by a user, as long as $\tilde{\Omega}(1/\varepsilon)$ users have $M_t/2$ samples each, the error at time $t$ is $\tilde{O}(1/\sqrt{t}+\sqrt{M}_t/t\varepsilon)$. This is a universal error guarantee which is valid for all arrival patterns of the users. Furthermore, it (almost) matches the existing lower bounds for the single-release setting at all time instants when users have contributed equal number of samples.

Robust Testing in High-Dimensional Sparse Models

We consider the problem of robustly testing the norm of a high-dimensional sparse signal vector under two different observation models. In the first model, we are given $n$ i.i.d. samples from the distribution $\mathcal{N}\left(\theta,I_d\right)$ (with unknown $\theta$), of which a small fraction has been arbitrarily corrupted. Under the promise that $\|\theta\|_0\le s$, we want to correctly distinguish whether $\|\theta\|_2=0$ or $\|\theta\|_2>\gamma$, for some input parameter $\gamma>0$. We show that any algorithm for this task requires $n=\Omega\left(s\log\frac{ed}{s}\right)$ samples, which is tight up to logarithmic factors. We also extend our results to other common notions of sparsity, namely, $\|\theta\|_q\le s$ for any $0 < q < 2$. In the second observation model that we consider, the data is generated according to a sparse linear regression model, where the covariates are i.i.d. Gaussian and the regression coefficient (signal) is known to be $s$-sparse. Here too we assume that an $\epsilon$-fraction of the data is arbitrarily corrupted. We show that any algorithm that reliably tests the norm of the regression coefficient requires at least $n=\Omega\left(\min(s\log d,{1}/{\gamma^4})\right)$ samples. Our results show that the complexity of testing in these two settings significantly increases under robustness constraints. This is in line with the recent observations made in robust mean testing and robust covariance testing.

An MCMC Method to Sample from Lattice Distributions

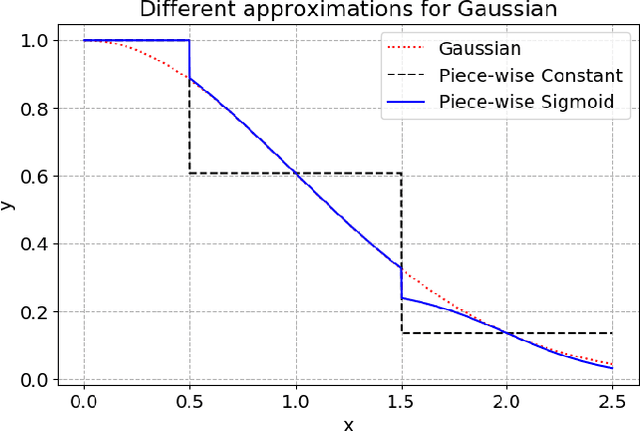
We introduce a Markov Chain Monte Carlo (MCMC) algorithm to generate samples from probability distributions supported on a $d$-dimensional lattice $\Lambda = \mathbf{B}\mathbb{Z}^d$, where $\mathbf{B}$ is a full-rank matrix. Specifically, we consider lattice distributions $P_\Lambda$ in which the probability at a lattice point is proportional to a given probability density function, $f$, evaluated at that point. To generate samples from $P_\Lambda$, it suffices to draw samples from a pull-back measure $P_{\mathbb{Z}^d}$ defined on the integer lattice. The probability of an integer lattice point under $P_{\mathbb{Z}^d}$ is proportional to the density function $\pi = |\det(\mathbf{B})|f\circ \mathbf{B}$. The algorithm we present in this paper for sampling from $P_{\mathbb{Z}^d}$ is based on the Metropolis-Hastings framework. In particular, we use $\pi$ as the proposal distribution and calculate the Metropolis-Hastings acceptance ratio for a well-chosen target distribution. We can use any method, denoted by ALG, that ideally draws samples from the probability density $\pi$, to generate a proposed state. The target distribution is a piecewise sigmoidal distribution, chosen such that the coordinate-wise rounding of a sample drawn from the target distribution gives a sample from $P_{\mathbb{Z}^d}$. When ALG is ideal, we show that our algorithm is uniformly ergodic if $-\log(\pi)$ satisfies a gradient Lipschitz condition.