Hidden Poison: Machine Unlearning Enables Camouflaged Poisoning Attacks

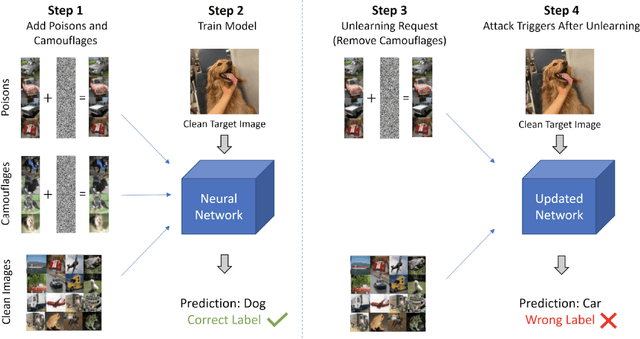
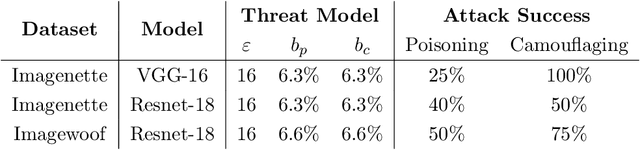
We introduce camouflaged data poisoning attacks, a new attack vector that arises in the context of machine unlearning and other settings when model retraining may be induced. An adversary first adds a few carefully crafted points to the training dataset such that the impact on the model's predictions is minimal. The adversary subsequently triggers a request to remove a subset of the introduced points at which point the attack is unleashed and the model's predictions are negatively affected. In particular, we consider clean-label targeted attacks (in which the goal is to cause the model to misclassify a specific test point) on datasets including CIFAR-10, Imagenette, and Imagewoof. This attack is realized by constructing camouflage datapoints that mask the effect of a poisoned dataset.

Discrete Distribution Estimation under User-level Local Differential Privacy

We study discrete distribution estimation under user-level local differential privacy (LDP). In user-level $\varepsilon$-LDP, each user has $m\ge1$ samples and the privacy of all $m$ samples must be preserved simultaneously. We resolve the following dilemma: While on the one hand having more samples per user should provide more information about the underlying distribution, on the other hand, guaranteeing the privacy of all $m$ samples should make the estimation task more difficult. We obtain tight bounds for this problem under almost all parameter regimes. Perhaps surprisingly, we show that in suitable parameter regimes, having $m$ samples per user is equivalent to having $m$ times more users, each with only one sample. Our results demonstrate interesting phase transitions for $m$ and the privacy parameter $\varepsilon$ in the estimation risk. Finally, connecting with recent results on shuffled DP, we show that combined with random shuffling, our algorithm leads to optimal error guarantees (up to logarithmic factors) under the central model of user-level DP in certain parameter regimes. We provide several simulations to verify our theoretical findings.

The Role of Interactivity in Structured Estimation

We study high-dimensional sparse estimation under three natural constraints: communication constraints, local privacy constraints, and linear measurements (compressive sensing). Without sparsity assumptions, it has been established that interactivity cannot improve the minimax rates of estimation under these information constraints. The question of whether interactivity helps with natural inference tasks has been a topic of active research. We settle this question in the affirmative for the prototypical problems of high-dimensional sparse mean estimation and compressive sensing, by demonstrating a gap between interactive and noninteractive protocols. We further establish that the gap increases when we have more structured sparsity: for block sparsity this gap can be as large as polynomial in the dimensionality. Thus, the more structured the sparsity is, the greater is the advantage of interaction. Proving the lower bounds requires a careful breaking of a sum of correlated random variables into independent components using Baranyai's theorem on decomposition of hypergraphs, which might be of independent interest.

Robust Estimation for Random Graphs

We study the problem of robustly estimating the parameter $p$ of an Erd\H{o}s-R\'enyi random graph on $n$ nodes, where a $\gamma$ fraction of nodes may be adversarially corrupted. After showing the deficiencies of canonical estimators, we design a computationally-efficient spectral algorithm which estimates $p$ up to accuracy $\tilde O(\sqrt{p(1-p)}/n + \gamma\sqrt{p(1-p)} /\sqrt{n}+ \gamma/n)$ for $\gamma < 1/60$. Furthermore, we give an inefficient algorithm with similar accuracy for all $\gamma <1/2$, the information-theoretic limit. Finally, we prove a nearly-matching statistical lower bound, showing that the error of our algorithms is optimal up to logarithmic factors.

Principal Bit Analysis: Autoencoding with Schur-Concave Loss

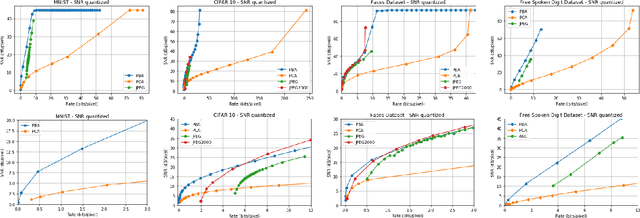
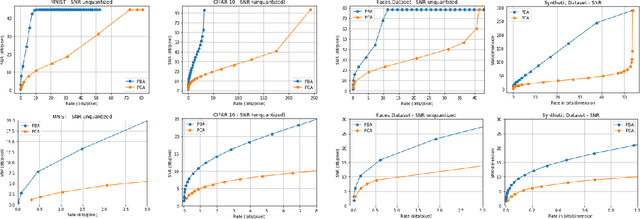
We consider a linear autoencoder in which the latent variables are quantized, or corrupted by noise, and the constraint is Schur-concave in the set of latent variances. Although finding the optimal encoder/decoder pair for this setup is a nonconvex optimization problem, we show that decomposing the source into its principal components is optimal. If the constraint is strictly Schur-concave and the empirical covariance matrix has only simple eigenvalues, then any optimal encoder/decoder must decompose the source in this way. As one application, we consider a strictly Schur-concave constraint that estimates the number of bits needed to represent the latent variables under fixed-rate encoding, a setup that we call \emph{Principal Bit Analysis (PBA)}. This yields a practical, general-purpose, fixed-rate compressor that outperforms existing algorithms. As a second application, we show that a prototypical autoencoder-based variable-rate compressor is guaranteed to decompose the source into its principal components.

Robust Testing and Estimation under Manipulation Attacks

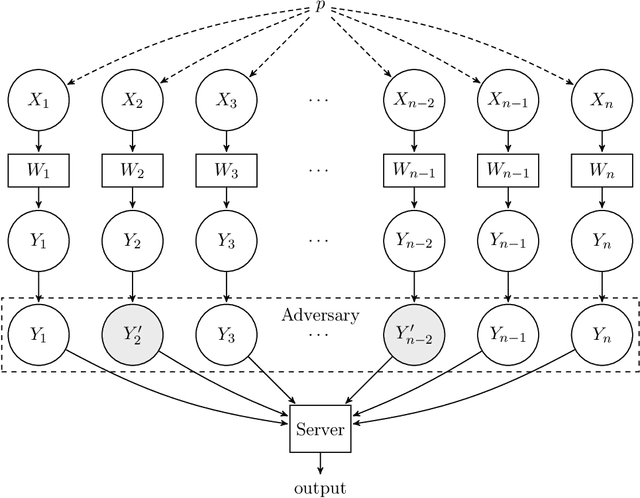
We study robust testing and estimation of discrete distributions in the strong contamination model. We consider both the "centralized setting" and the "distributed setting with information constraints" including communication and local privacy (LDP) constraints. Our technique relates the strength of manipulation attacks to the earth-mover distance using Hamming distance as the metric between messages(samples) from the users. In the centralized setting, we provide optimal error bounds for both learning and testing. Our lower bounds under local information constraints build on the recent lower bound methods in distributed inference. In the communication constrained setting, we develop novel algorithms based on random hashing and an $\ell_1/\ell_1$ isometry.

Remember What You Want to Forget: Algorithms for Machine Unlearning

We study the problem of forgetting datapoints from a learnt model. In this case, the learner first receives a dataset $S$ drawn i.i.d. from an unknown distribution, and outputs a predictor $w$ that performs well on unseen samples from that distribution. However, at some point in the future, any training data point $z \in S$ can request to be unlearned, thus prompting the learner to modify its output predictor while still ensuring the same accuracy guarantees. In our work, we initiate a rigorous study of machine unlearning in the population setting, where the goal is to maintain performance on the unseen test loss. We then provide unlearning algorithms for convex loss functions. For the setting of convex losses, we provide an unlearning algorithm that can delete up to $O(n/d^{1/4})$ samples, where $d$ is the problem dimension. In comparison, in general, differentially private learningv(which implies unlearning) only guarantees deletion of $O(n/d^{1/2})$ samples. This shows that unlearning is at least polynomially more efficient than learning privately in terms of dependence on $d$ in the deletion capacity.

General lower bounds for interactive high-dimensional estimation under information constraints

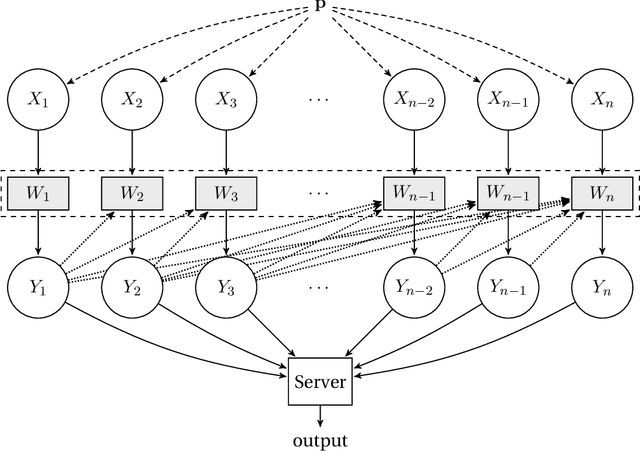
We consider the task of distributed parameter estimation using sequentially interactive protocols subject to local information constraints such as bandwidth limitations, local differential privacy, and restricted measurements. We provide a general framework enabling us to derive a variety of (tight) minimax lower bounds under different parametric families of distributions, both continuous and discrete, under any $\ell_p$ loss. Our lower bound framework is versatile, and yields "plug-and-play" bounds that are widely applicable to a large range of estimation problems. In particular, our approach recovers bounds obtained using data processing inequalities and Cram\'er-Rao bounds, two other alternative approaches for proving lower bounds in our setting of interest. Further, for the families considered, we complement our lower bounds with matching upper bounds.

Estimating Sparse Discrete Distributions Under Local Privacy and Communication Constraints

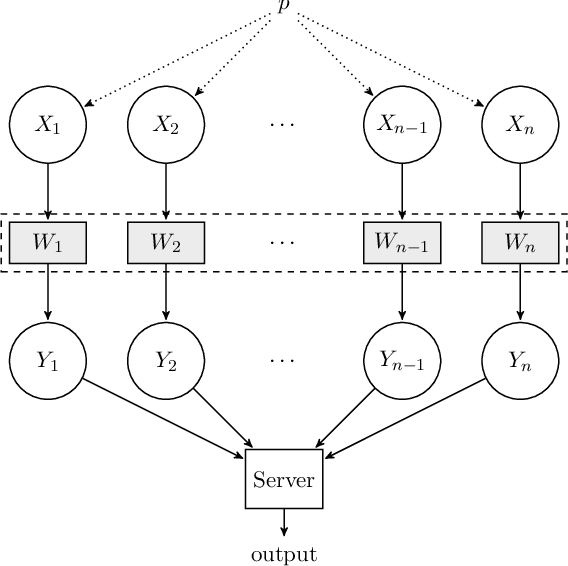
We consider the task of estimating sparse discrete distributions under local differential privacy and communication constraints. Under local privacy constraints, we present a sample-optimal private-coin scheme that only sends a one-bit message per user. For communication constraints, we present a public-coin scheme based on random hashing functions, which we prove is optimal up to logarithmic factors. Our results show that the sample complexity only depends logarithmically on the ambient dimension, thus providing significant improvement in sample complexity under sparsity assumptions. Our lower bounds are based on a recently proposed chi-squared contraction method.

Interactive Inference under Information Constraints

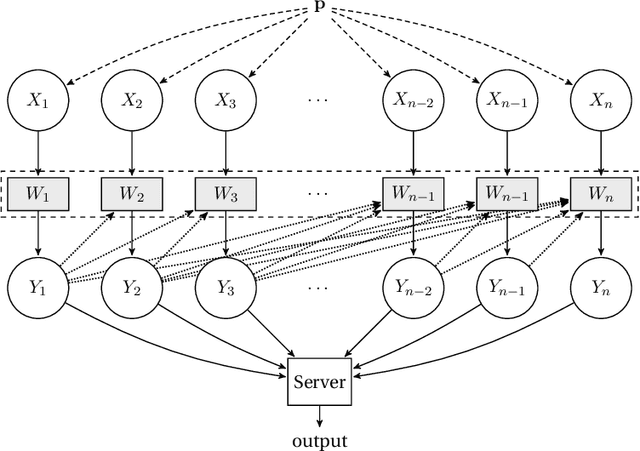
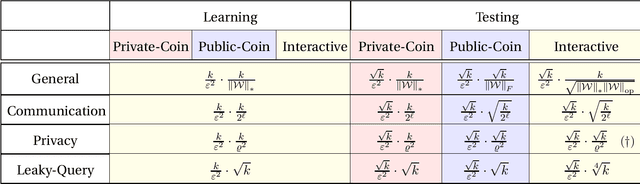
We consider distributed inference using sequentially interactive protocols. We obtain lower bounds on the minimax sample complexity of interactive protocols under local information constraints, a broad family of resource constraints which captures communication constraints, local differential privacy, and noisy binary queries as special cases. We focus on the inference tasks of learning (density estimation) and identity testing (goodness-of-fit) for discrete distributions under total variation distance, and establish general lower bounds that take into account the local constraints modeled as a channel family. Our main technical contribution is an approach to handle the correlation that builds due to interactivity and quantifies how effectively one can exploit this correlation in spite of the local constraints. Using this, we fill gaps in some prior works and characterize the optimal sample complexity of learning and testing discrete distributions under total variation distance, for both communication and local differential privacy constraints. Prior to our work, this was known only for the problem of testing under local privacy constraints (Amin, Joseph, and Mao (2020); Berrett and Butucea (2020)). Our results show that interactivity does not help for learning or testing under these two constraints. Finally, we provide the first instance of a natural family of "leaky query" local constraints under which interactive protocols strictly outperform the noninteractive ones for distribution testing.