Robust Testing and Estimation under Manipulation Attacks
Paper and Code
Apr 21, 2021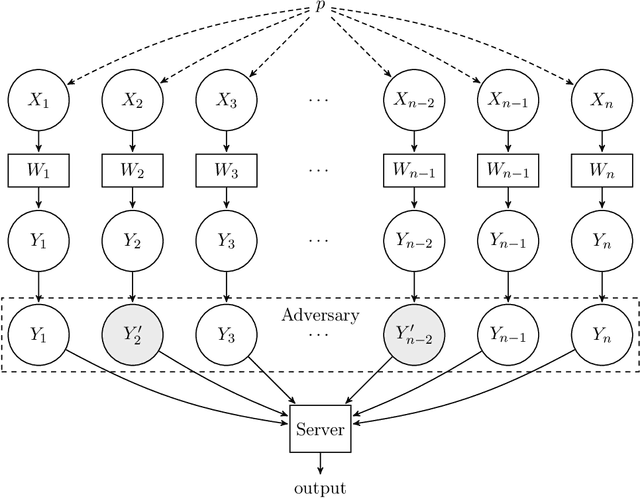

We study robust testing and estimation of discrete distributions in the strong contamination model. We consider both the "centralized setting" and the "distributed setting with information constraints" including communication and local privacy (LDP) constraints. Our technique relates the strength of manipulation attacks to the earth-mover distance using Hamming distance as the metric between messages(samples) from the users. In the centralized setting, we provide optimal error bounds for both learning and testing. Our lower bounds under local information constraints build on the recent lower bound methods in distributed inference. In the communication constrained setting, we develop novel algorithms based on random hashing and an $\ell_1/\ell_1$ isometry.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge