BaseReward: A Strong Baseline for Multimodal Reward Model

The rapid advancement of Multimodal Large Language Models (MLLMs) has made aligning them with human preferences a critical challenge. Reward Models (RMs) are a core technology for achieving this goal, but a systematic guide for building state-of-the-art Multimodal Reward Models (MRMs) is currently lacking in both academia and industry. Through exhaustive experimental analysis, this paper aims to provide a clear ``recipe'' for constructing high-performance MRMs. We systematically investigate every crucial component in the MRM development pipeline, including \textit{reward modeling paradigms} (e.g., Naive-RM, Critic-based RM, and Generative RM), \textit{reward head architecture}, \textit{training strategies}, \textit{data curation} (covering over ten multimodal and text-only preference datasets), \textit{backbone model} and \textit{model scale}, and \textit{ensemble methods}. Based on these experimental insights, we introduce \textbf{BaseReward}, a powerful and efficient baseline for multimodal reward modeling. BaseReward adopts a simple yet effective architecture, built upon a {Qwen2.5-VL} backbone, featuring an optimized two-layer reward head, and is trained on a carefully curated mixture of high-quality multimodal and text-only preference data. Our results show that BaseReward establishes a new SOTA on major benchmarks such as MM-RLHF-Reward Bench, VL-Reward Bench, and Multimodal Reward Bench, outperforming previous models. Furthermore, to validate its practical utility beyond static benchmarks, we integrate BaseReward into a real-world reinforcement learning pipeline, successfully enhancing an MLLM's performance across various perception, reasoning, and conversational tasks. This work not only delivers a top-tier MRM but, more importantly, provides the community with a clear, empirically-backed guide for developing robust reward models for the next generation of MLLMs.

11Plus-Bench: Demystifying Multimodal LLM Spatial Reasoning with Cognitive-Inspired Analysis

For human cognitive process, spatial reasoning and perception are closely entangled, yet the nature of this interplay remains underexplored in the evaluation of multimodal large language models (MLLMs). While recent MLLM advancements show impressive performance on reasoning, their capacity for human-like spatial cognition remains an open question. In this work, we introduce a systematic evaluation framework to assess the spatial reasoning abilities of state-of-the-art MLLMs relative to human performance. Central to our work is 11Plus-Bench, a high-quality benchmark derived from realistic standardized spatial aptitude tests. 11Plus-Bench also features fine-grained expert annotations of both perceptual complexity and reasoning process, enabling detailed instance-level analysis of model behavior. Through extensive experiments across 14 MLLMs and human evaluation, we find that current MLLMs exhibit early signs of spatial cognition. Despite a large performance gap compared to humans, MLLMs' cognitive profiles resemble those of humans in that cognitive effort correlates strongly with reasoning-related complexity. However, instance-level performance in MLLMs remains largely random, whereas human correctness is highly predictable and shaped by abstract pattern complexity. These findings highlight both emerging capabilities and limitations in current MLLMs' spatial reasoning capabilities and provide actionable insights for advancing model design.

Memory-Efficient Differentially Private Training with Gradient Random Projection

Differential privacy (DP) protects sensitive data during neural network training, but standard methods like DP-Adam suffer from high memory overhead due to per-sample gradient clipping, limiting scalability. We introduce DP-GRAPE (Gradient RAndom ProjEction), a DP training method that significantly reduces memory usage while maintaining utility on par with first-order DP approaches. Rather than directly applying DP to GaLore, DP-GRAPE introduces three key modifications: (1) gradients are privatized after projection, (2) random Gaussian matrices replace SVD-based subspaces, and (3) projection is applied during backpropagation. These contributions eliminate the need for costly SVD computations, enable substantial memory savings, and lead to improved utility. Despite operating in lower-dimensional subspaces, our theoretical analysis shows that DP-GRAPE achieves a privacy-utility trade-off comparable to DP-SGD. Our extensive empirical experiments show that DP-GRAPE can reduce the memory footprint of DP training without sacrificing accuracy or training time. In particular, DP-GRAPE reduces memory usage by over 63% when pre-training Vision Transformers and over 70% when fine-tuning RoBERTa-Large as compared to DP-Adam, while achieving similar performance. We further demonstrate that DP-GRAPE scales to fine-tuning large models such as OPT with up to 6.7 billion parameters.

A Call for New Recipes to Enhance Spatial Reasoning in MLLMs

Multimodal Large Language Models (MLLMs) have demonstrated impressive performance in general vision-language tasks. However, recent studies have exposed critical limitations in their spatial reasoning capabilities. This deficiency in spatial reasoning significantly constrains MLLMs' ability to interact effectively with the physical world, thereby limiting their broader applications. We argue that spatial reasoning capabilities will not naturally emerge from merely scaling existing architectures and training methodologies. Instead, this challenge demands dedicated attention to fundamental modifications in the current MLLM development approach. In this position paper, we first establish a comprehensive framework for spatial reasoning within the context of MLLMs. We then elaborate on its pivotal role in real-world applications. Through systematic analysis, we examine how individual components of the current methodology-from training data to reasoning mechanisms-influence spatial reasoning capabilities. This examination reveals critical limitations while simultaneously identifying promising avenues for advancement. Our work aims to direct the AI research community's attention toward these crucial yet underexplored aspects. By highlighting these challenges and opportunities, we seek to catalyze progress toward achieving human-like spatial reasoning capabilities in MLLMs.

Imagine while Reasoning in Space: Multimodal Visualization-of-Thought

Chain-of-Thought (CoT) prompting has proven highly effective for enhancing complex reasoning in Large Language Models (LLMs) and Multimodal Large Language Models (MLLMs). Yet, it struggles in complex spatial reasoning tasks. Nonetheless, human cognition extends beyond language alone, enabling the remarkable capability to think in both words and images. Inspired by this mechanism, we propose a new reasoning paradigm, Multimodal Visualization-of-Thought (MVoT). It enables visual thinking in MLLMs by generating image visualizations of their reasoning traces. To ensure high-quality visualization, we introduce token discrepancy loss into autoregressive MLLMs. This innovation significantly improves both visual coherence and fidelity. We validate this approach through several dynamic spatial reasoning tasks. Experimental results reveal that MVoT demonstrates competitive performance across tasks. Moreover, it exhibits robust and reliable improvements in the most challenging scenarios where CoT fails. Ultimately, MVoT establishes new possibilities for complex reasoning tasks where visual thinking can effectively complement verbal reasoning.

TimeRAF: Retrieval-Augmented Foundation model for Zero-shot Time Series Forecasting

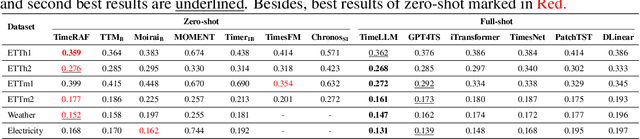
Time series forecasting plays a crucial role in data mining, driving rapid advancements across numerous industries. With the emergence of large models, time series foundation models (TSFMs) have exhibited remarkable generalization capabilities, such as zero-shot learning, through large-scale pre-training. Meanwhile, Retrieval-Augmented Generation (RAG) methods have been widely employed to enhance the performance of foundation models on unseen data, allowing models to access to external knowledge. In this paper, we introduce TimeRAF, a Retrieval-Augmented Forecasting model that enhance zero-shot time series forecasting through retrieval-augmented techniques. We develop customized time series knowledge bases that are tailored to the specific forecasting tasks. TimeRAF employs an end-to-end learnable retriever to extract valuable information from the knowledge base. Additionally, we propose Channel Prompting for knowledge integration, which effectively extracts relevant information from the retrieved knowledge along the channel dimension. Extensive experiments demonstrate the effectiveness of our model, showing significant improvement across various domains and datasets.

MME-RealWorld: Could Your Multimodal LLM Challenge High-Resolution Real-World Scenarios that are Difficult for Humans?

Comprehensive evaluation of Multimodal Large Language Models (MLLMs) has recently garnered widespread attention in the research community. However, we observe that existing benchmarks present several common barriers that make it difficult to measure the significant challenges that models face in the real world, including: 1) small data scale leads to a large performance variance; 2) reliance on model-based annotations results in restricted data quality; 3) insufficient task difficulty, especially caused by the limited image resolution. To tackle these issues, we introduce MME-RealWorld. Specifically, we collect more than $300$K images from public datasets and the Internet, filtering $13,366$ high-quality images for annotation. This involves the efforts of professional $25$ annotators and $7$ experts in MLLMs, contributing to $29,429$ question-answer pairs that cover $43$ subtasks across $5$ real-world scenarios, extremely challenging even for humans. As far as we know, MME-RealWorld is the largest manually annotated benchmark to date, featuring the highest resolution and a targeted focus on real-world applications. We further conduct a thorough evaluation involving $28$ prominent MLLMs, such as GPT-4o, Gemini 1.5 Pro, and Claude 3.5 Sonnet. Our results show that even the most advanced models struggle with our benchmarks, where none of them reach $60\%$ accuracy. The challenges of perceiving high-resolution images and understanding complex real-world scenarios remain urgent issues to be addressed. The data and evaluation code are released at https://mme-realworld.github.io/ .

Statler: State-Maintaining Language Models for Embodied Reasoning

Large language models (LLMs) provide a promising tool that enable robots to perform complex robot reasoning tasks. However, the limited context window of contemporary LLMs makes reasoning over long time horizons difficult. Embodied tasks such as those that one might expect a household robot to perform typically require that the planner consider information acquired a long time ago (e.g., properties of the many objects that the robot previously encountered in the environment). Attempts to capture the world state using an LLM's implicit internal representation is complicated by the paucity of task- and environment-relevant information available in a robot's action history, while methods that rely on the ability to convey information via the prompt to the LLM are subject to its limited context window. In this paper, we propose Statler, a framework that endows LLMs with an explicit representation of the world state as a form of ``memory'' that is maintained over time. Integral to Statler is its use of two instances of general LLMs -- a world-model reader and a world-model writer -- that interface with and maintain the world state. By providing access to this world state ``memory'', Statler improves the ability of existing LLMs to reason over longer time horizons without the constraint of context length. We evaluate the effectiveness of our approach on three simulated table-top manipulation domains and a real robot domain, and show that it improves the state-of-the-art in LLM-based robot reasoning. Project website: https://statler-lm.github.io/

DP-HyPO: An Adaptive Private Hyperparameter Optimization Framework

Hyperparameter optimization, also known as hyperparameter tuning, is a widely recognized technique for improving model performance. Regrettably, when training private ML models, many practitioners often overlook the privacy risks associated with hyperparameter optimization, which could potentially expose sensitive information about the underlying dataset. Currently, the sole existing approach to allow privacy-preserving hyperparameter optimization is to uniformly and randomly select hyperparameters for a number of runs, subsequently reporting the best-performing hyperparameter. In contrast, in non-private settings, practitioners commonly utilize "adaptive" hyperparameter optimization methods such as Gaussian process-based optimization, which select the next candidate based on information gathered from previous outputs. This substantial contrast between private and non-private hyperparameter optimization underscores a critical concern. In our paper, we introduce DP-HyPO, a pioneering framework for "adaptive" private hyperparameter optimization, aiming to bridge the gap between private and non-private hyperparameter optimization. To accomplish this, we provide a comprehensive differential privacy analysis of our framework. Furthermore, we empirically demonstrate the effectiveness of DP-HyPO on a diverse set of real-world and synthetic datasets.

Federated Linear Contextual Bandits with User-level Differential Privacy

This paper studies federated linear contextual bandits under the notion of user-level differential privacy (DP). We first introduce a unified federated bandits framework that can accommodate various definitions of DP in the sequential decision-making setting. We then formally introduce user-level central DP (CDP) and local DP (LDP) in the federated bandits framework, and investigate the fundamental trade-offs between the learning regrets and the corresponding DP guarantees in a federated linear contextual bandits model. For CDP, we propose a federated algorithm termed as $\texttt{ROBIN}$ and show that it is near-optimal in terms of the number of clients $M$ and the privacy budget $\varepsilon$ by deriving nearly-matching upper and lower regret bounds when user-level DP is satisfied. For LDP, we obtain several lower bounds, indicating that learning under user-level $(\varepsilon,\delta)$-LDP must suffer a regret blow-up factor at least $\min\{1/\varepsilon,M\}$ or $\min\{1/\sqrt{\varepsilon},\sqrt{M}\}$ under different conditions.