Locally Private Sampling with Public Data

Local differential privacy (LDP) is increasingly employed in privacy-preserving machine learning to protect user data before sharing it with an untrusted aggregator. Most LDP methods assume that users possess only a single data record, which is a significant limitation since users often gather extensive datasets (e.g., images, text, time-series data) and frequently have access to public datasets. To address this limitation, we propose a locally private sampling framework that leverages both the private and public datasets of each user. Specifically, we assume each user has two distributions: $p$ and $q$ that represent their private dataset and the public dataset, respectively. The objective is to design a mechanism that generates a private sample approximating $p$ while simultaneously preserving $q$. We frame this objective as a minimax optimization problem using $f$-divergence as the utility measure. We fully characterize the minimax optimal mechanisms for general $f$-divergences provided that $p$ and $q$ are discrete distributions. Remarkably, we demonstrate that this optimal mechanism is universal across all $f$-divergences. Experiments validate the effectiveness of our minimax optimal sampler compared to the state-of-the-art locally private sampler.

Exactly Minimax-Optimal Locally Differentially Private Sampling

The sampling problem under local differential privacy has recently been studied with potential applications to generative models, but a fundamental analysis of its privacy-utility trade-off (PUT) remains incomplete. In this work, we define the fundamental PUT of private sampling in the minimax sense, using the f-divergence between original and sampling distributions as the utility measure. We characterize the exact PUT for both finite and continuous data spaces under some mild conditions on the data distributions, and propose sampling mechanisms that are universally optimal for all f-divergences. Our numerical experiments demonstrate the superiority of our mechanisms over baselines, in terms of theoretical utilities for finite data space and of empirical utilities for continuous data space.

Differentially Private Fair Binary Classifications

In this work, we investigate binary classification under the constraints of both differential privacy and fairness. We first propose an algorithm based on the decoupling technique for learning a classifier with only fairness guarantee. This algorithm takes in classifiers trained on different demographic groups and generates a single classifier satisfying statistical parity. We then refine this algorithm to incorporate differential privacy. The performance of the final algorithm is rigorously examined in terms of privacy, fairness, and utility guarantees. Empirical evaluations conducted on the Adult and Credit Card datasets illustrate that our algorithm outperforms the state-of-the-art in terms of fairness guarantees, while maintaining the same level of privacy and utility.

Sample-Optimal Locally Private Hypothesis Selection and the Provable Benefits of Interactivity

We study the problem of hypothesis selection under the constraint of local differential privacy. Given a class $\mathcal{F}$ of $k$ distributions and a set of i.i.d. samples from an unknown distribution $h$, the goal of hypothesis selection is to pick a distribution $\hat{f}$ whose total variation distance to $h$ is comparable with the best distribution in $\mathcal{F}$ (with high probability). We devise an $\varepsilon$-locally-differentially-private ($\varepsilon$-LDP) algorithm that uses $\Theta\left(\frac{k}{\alpha^2\min \{\varepsilon^2,1\}}\right)$ samples to guarantee that $d_{TV}(h,\hat{f})\leq \alpha + 9 \min_{f\in \mathcal{F}}d_{TV}(h,f)$ with high probability. This sample complexity is optimal for $\varepsilon<1$, matching the lower bound of Gopi et al. (2020). All previously known algorithms for this problem required $\Omega\left(\frac{k\log k}{\alpha^2\min \{ \varepsilon^2 ,1\}} \right)$ samples to work. Moreover, our result demonstrates the power of interaction for $\varepsilon$-LDP hypothesis selection. Namely, it breaks the known lower bound of $\Omega\left(\frac{k\log k}{\alpha^2\min \{ \varepsilon^2 ,1\}} \right)$ for the sample complexity of non-interactive hypothesis selection. Our algorithm breaks this barrier using only $\Theta(\log \log k)$ rounds of interaction. To prove our results, we define the notion of \emph{critical queries} for a Statistical Query Algorithm (SQA) which may be of independent interest. Informally, an SQA is said to use a small number of critical queries if its success relies on the accuracy of only a small number of queries it asks. We then design an LDP algorithm that uses a smaller number of critical queries.

Privacy Loss of Noisy Stochastic Gradient Descent Might Converge Even for Non-Convex Losses

The Noisy-SGD algorithm is widely used for privately training machine learning models. Traditional privacy analyses of this algorithm assume that the internal state is publicly revealed, resulting in privacy loss bounds that increase indefinitely with the number of iterations. However, recent findings have shown that if the internal state remains hidden, then the privacy loss might remain bounded. Nevertheless, this remarkable result heavily relies on the assumption of (strong) convexity of the loss function. It remains an important open problem to further relax this condition while proving similar convergent upper bounds on the privacy loss. In this work, we address this problem for DP-SGD, a popular variant of Noisy-SGD that incorporates gradient clipping to limit the impact of individual samples on the training process. Our findings demonstrate that the privacy loss of projected DP-SGD converges exponentially fast, without requiring convexity or smoothness assumptions on the loss function. In addition, we analyze the privacy loss of regularized (unprojected) DP-SGD. To obtain these results, we directly analyze the hockey-stick divergence between coupled stochastic processes by relying on non-linear data processing inequalities.

Contraction of Locally Differentially Private Mechanisms

We investigate the contraction properties of locally differentially private mechanisms. More specifically, we derive tight upper bounds on the divergence between $PK$ and $QK$ output distributions of an $\epsilon$-LDP mechanism $K$ in terms of a divergence between the corresponding input distributions $P$ and $Q$, respectively. Our first main technical result presents a sharp upper bound on the $\chi^2$-divergence $\chi^2(PK\|QK)$ in terms of $\chi^2(P\|Q)$ and $\epsilon$. We also show that the same result holds for a large family of divergences, including KL-divergence and squared Hellinger distance. The second main technical result gives an upper bound on $\chi^2(PK\|QK)$ in terms of total variation distance $TV(P, Q)$ and $\epsilon$. We then utilize these bounds to establish locally private versions of the Cram\'er-Rao bound, Le Cam's, Assouad's, and the mutual information methods, which are powerful tools for bounding minimax estimation risks. These results are shown to lead to better privacy analyses than the state-of-the-arts in several statistical problems such as entropy and discrete distribution estimation, non-parametric density estimation, and hypothesis testing.

The Saddle-Point Accountant for Differential Privacy

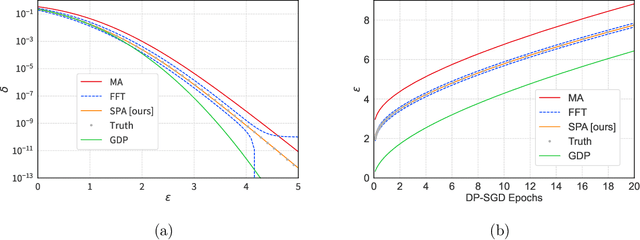
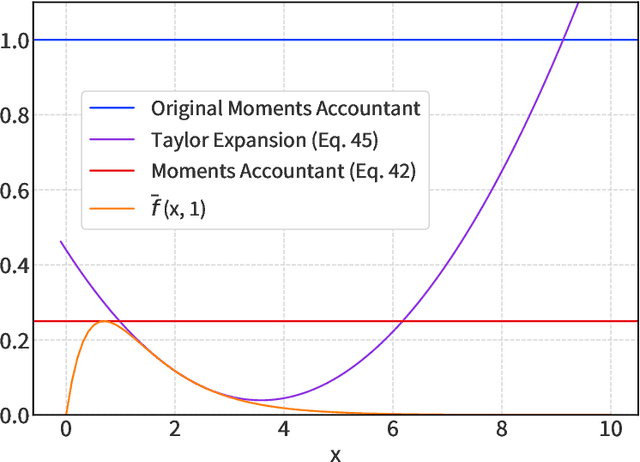
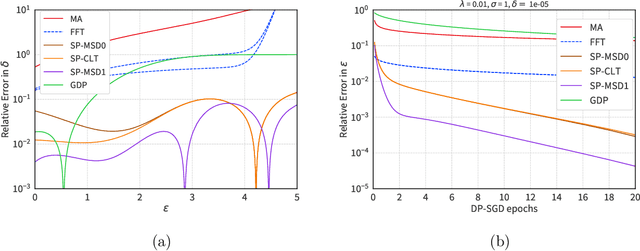
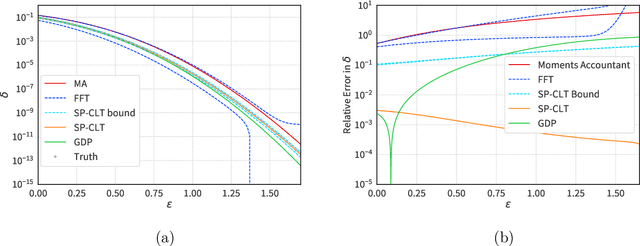
We introduce a new differential privacy (DP) accountant called the saddle-point accountant (SPA). SPA approximates privacy guarantees for the composition of DP mechanisms in an accurate and fast manner. Our approach is inspired by the saddle-point method -- a ubiquitous numerical technique in statistics. We prove rigorous performance guarantees by deriving upper and lower bounds for the approximation error offered by SPA. The crux of SPA is a combination of large-deviation methods with central limit theorems, which we derive via exponentially tilting the privacy loss random variables corresponding to the DP mechanisms. One key advantage of SPA is that it runs in constant time for the $n$-fold composition of a privacy mechanism. Numerical experiments demonstrate that SPA achieves comparable accuracy to state-of-the-art accounting methods with a faster runtime.

Cactus Mechanisms: Optimal Differential Privacy Mechanisms in the Large-Composition Regime

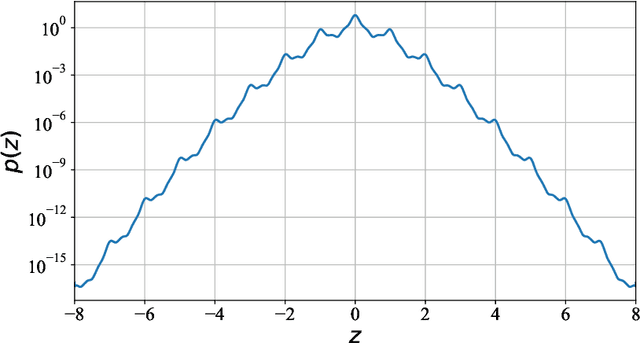
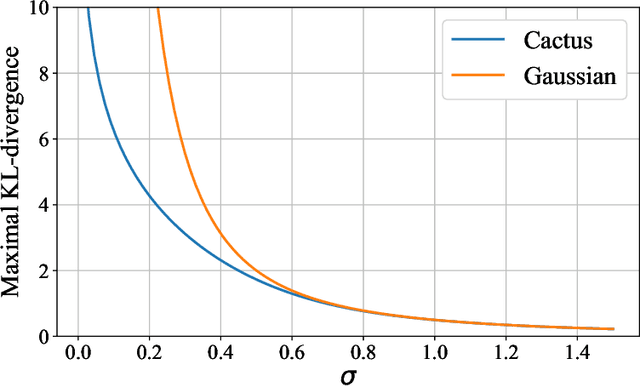
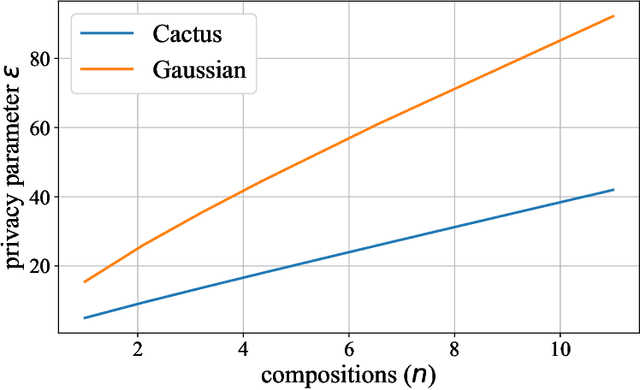
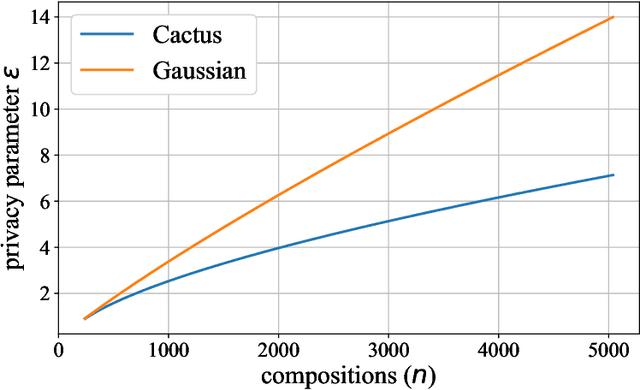
Most differential privacy mechanisms are applied (i.e., composed) numerous times on sensitive data. We study the design of optimal differential privacy mechanisms in the limit of a large number of compositions. As a consequence of the law of large numbers, in this regime the best privacy mechanism is the one that minimizes the Kullback-Leibler divergence between the conditional output distributions of the mechanism given two different inputs. We formulate an optimization problem to minimize this divergence subject to a cost constraint on the noise. We first prove that additive mechanisms are optimal. Since the optimization problem is infinite dimensional, it cannot be solved directly; nevertheless, we quantize the problem to derive near-optimal additive mechanisms that we call "cactus mechanisms" due to their shape. We show that our quantization approach can be arbitrarily close to an optimal mechanism. Surprisingly, for quadratic cost, the Gaussian mechanism is strictly sub-optimal compared to this cactus mechanism. Finally, we provide numerical results which indicate that cactus mechanism outperforms the Gaussian mechanism for a finite number of compositions.

Beyond Adult and COMPAS: Fairness in Multi-Class Prediction

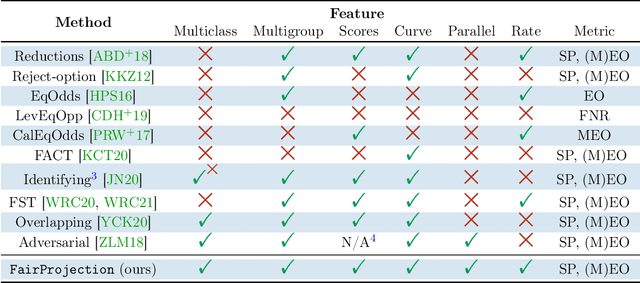
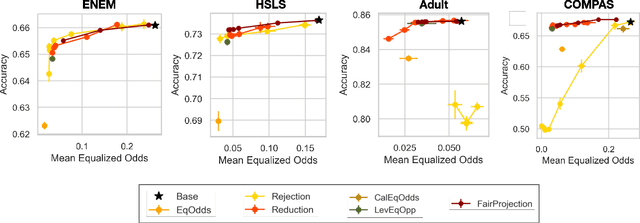
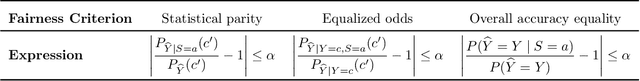
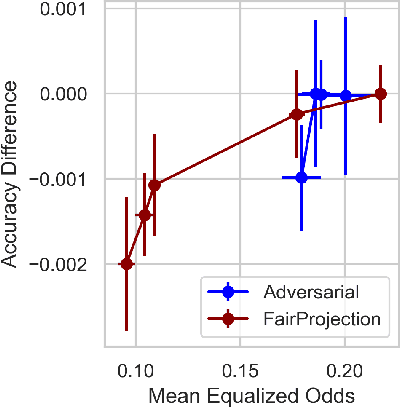
We consider the problem of producing fair probabilistic classifiers for multi-class classification tasks. We formulate this problem in terms of "projecting" a pre-trained (and potentially unfair) classifier onto the set of models that satisfy target group-fairness requirements. The new, projected model is given by post-processing the outputs of the pre-trained classifier by a multiplicative factor. We provide a parallelizable iterative algorithm for computing the projected classifier and derive both sample complexity and convergence guarantees. Comprehensive numerical comparisons with state-of-the-art benchmarks demonstrate that our approach maintains competitive performance in terms of accuracy-fairness trade-off curves, while achieving favorable runtime on large datasets. We also evaluate our method at scale on an open dataset with multiple classes, multiple intersectional protected groups, and over 1M samples.

Local Differential Privacy Is Equivalent to Contraction of $E_γ$-Divergence

We investigate the local differential privacy (LDP) guarantees of a randomized privacy mechanism via its contraction properties. We first show that LDP constraints can be equivalently cast in terms of the contraction coefficient of the $E_\gamma$-divergence. We then use this equivalent formula to express LDP guarantees of privacy mechanisms in terms of contraction coefficients of arbitrary $f$-divergences. When combined with standard estimation-theoretic tools (such as Le Cam's and Fano's converse methods), this result allows us to study the trade-off between privacy and utility in several testing and minimax and Bayesian estimation problems.