GeoClip: Geometry-Aware Clipping for Differentially Private SGD

Differentially private stochastic gradient descent (DP-SGD) is the most widely used method for training machine learning models with provable privacy guarantees. A key challenge in DP-SGD is setting the per-sample gradient clipping threshold, which significantly affects the trade-off between privacy and utility. While recent adaptive methods improve performance by adjusting this threshold during training, they operate in the standard coordinate system and fail to account for correlations across the coordinates of the gradient. We propose GeoClip, a geometry-aware framework that clips and perturbs gradients in a transformed basis aligned with the geometry of the gradient distribution. GeoClip adaptively estimates this transformation using only previously released noisy gradients, incurring no additional privacy cost. We provide convergence guarantees for GeoClip and derive a closed-form solution for the optimal transformation that minimizes the amount of noise added while keeping the probability of gradient clipping under control. Experiments on both tabular and image datasets demonstrate that GeoClip consistently outperforms existing adaptive clipping methods under the same privacy budget.

Reveal-or-Obscure: A Differentially Private Sampling Algorithm for Discrete Distributions

We introduce a differentially private (DP) algorithm called reveal-or-obscure (ROO) to generate a single representative sample from a dataset of $n$ observations drawn i.i.d. from an unknown discrete distribution $P$. Unlike methods that add explicit noise to the estimated empirical distribution, ROO achieves $\epsilon$-differential privacy by randomly choosing whether to "reveal" or "obscure" the empirical distribution. While ROO is structurally identical to Algorithm 1 proposed by Cheu and Nayak (arXiv:2412.10512), we prove a strictly better bound on the sampling complexity than that established in Theorem 12 of (arXiv:2412.10512). To further improve the privacy-utility trade-off, we propose a novel generalized sampling algorithm called Data-Specific ROO (DS-ROO), where the probability of obscuring the empirical distribution of the dataset is chosen adaptively. We prove that DS-ROO satisfies $\epsilon$-DP, and provide empirical evidence that DS-ROO can achieve better utility under the same privacy budget of vanilla ROO.

VALID: a Validated Algorithm for Learning in Decentralized Networks with Possible Adversarial Presence

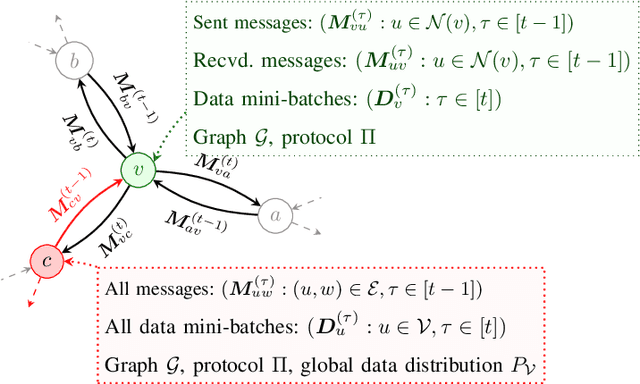
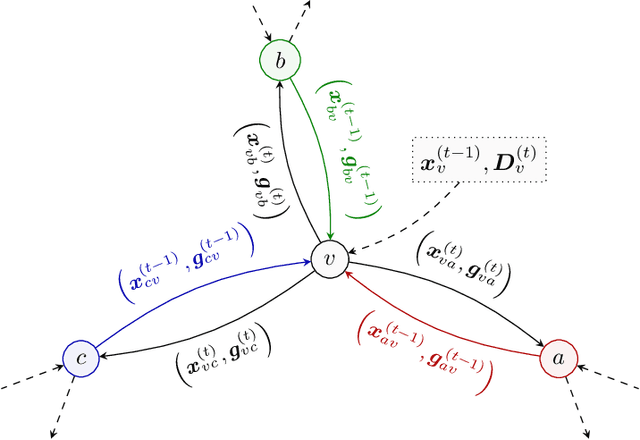
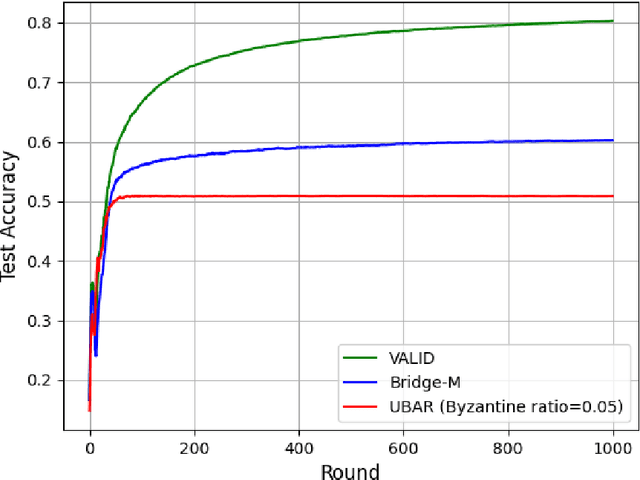
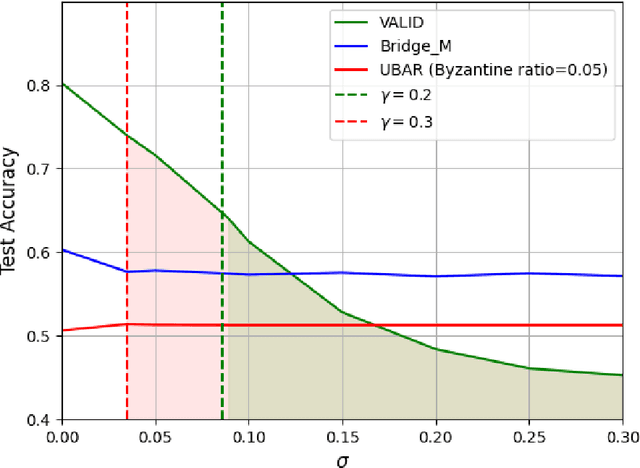
We introduce the paradigm of validated decentralized learning for undirected networks with heterogeneous data and possible adversarial infiltration. We require (a) convergence to a global empirical loss minimizer when adversaries are absent, and (b) either detection of adversarial presence of convergence to an admissible consensus irrespective of the adversarial configuration. To this end, we propose the VALID protocol which, to the best of our knowledge, is the first to achieve a validated learning guarantee. Moreover, VALID offers an O(1/T) convergence rate (under pertinent regularity assumptions), and computational and communication complexities comparable to non-adversarial distributed stochastic gradient descent. Remarkably, VALID retains optimal performance metrics in adversary-free environments, sidestepping the robustness penalties observed in prior byzantine-robust methods. A distinctive aspect of our study is a heterogeneity metric based on the norms of individual agents' gradients computed at the global empirical loss minimizer. This not only provides a natural statistic for detecting significant byzantine disruptions but also allows us to prove the optimality of VALID in wide generality. Lastly, our numerical results reveal that, in the absence of adversaries, VALID converges faster than state-of-the-art byzantine robust algorithms, while when adversaries are present, VALID terminates with each honest either converging to an admissible consensus of declaring adversarial presence in the network.

An Adversarial Approach to Evaluating the Robustness of Event Identification Models

Intelligent machine learning approaches are finding active use for event detection and identification that allow real-time situational awareness. Yet, such machine learning algorithms have been shown to be susceptible to adversarial attacks on the incoming telemetry data. This paper considers a physics-based modal decomposition method to extract features for event classification and focuses on interpretable classifiers including logistic regression and gradient boosting to distinguish two types of events: load loss and generation loss. The resulting classifiers are then tested against an adversarial algorithm to evaluate their robustness. The adversarial attack is tested in two settings: the white box setting, wherein the attacker knows exactly the classification model; and the gray box setting, wherein the attacker has access to historical data from the same network as was used to train the classifier, but does not know the classification model. Thorough experiments on the synthetic South Carolina 500-bus system highlight that a relatively simpler model such as logistic regression is more susceptible to adversarial attacks than gradient boosting.

A Semi-Supervised Approach for Power System Event Identification

Event identification is increasingly recognized as crucial for enhancing the reliability, security, and stability of the electric power system. With the growing deployment of Phasor Measurement Units (PMUs) and advancements in data science, there are promising opportunities to explore data-driven event identification via machine learning classification techniques. However, obtaining accurately-labeled eventful PMU data samples remains challenging due to its labor-intensive nature and uncertainty about the event type (class) in real-time. Thus, it is natural to use semi-supervised learning techniques, which make use of both labeled and unlabeled samples. %We propose a novel semi-supervised framework to assess the effectiveness of incorporating unlabeled eventful samples to enhance existing event identification methodologies. We evaluate three categories of classical semi-supervised approaches: (i) self-training, (ii) transductive support vector machines (TSVM), and (iii) graph-based label spreading (LS) method. Our approach characterizes events using physically interpretable features extracted from modal analysis of synthetic eventful PMU data. In particular, we focus on the identification of four event classes whose identification is crucial for grid operations. We have developed and publicly shared a comprehensive Event Identification package which consists of three aspects: data generation, feature extraction, and event identification with limited labels using semi-supervised methodologies. Using this package, we generate and evaluate eventful PMU data for the South Carolina synthetic network. Our evaluation consistently demonstrates that graph-based LS outperforms the other two semi-supervised methods that we consider, and can noticeably improve event identification performance relative to the setting with only a small number of labeled samples.

Robust Model Selection of Non Tree-Structured Gaussian Graphical Models

We consider the problem of learning the structure underlying a Gaussian graphical model when the variables (or subsets thereof) are corrupted by independent noise. A recent line of work establishes that even for tree-structured graphical models, only partial structure recovery is possible and goes on to devise algorithms to identify the structure up to an (unavoidable) equivalence class of trees. We extend these results beyond trees and consider the model selection problem under noise for non tree-structured graphs, as tree graphs cannot model several real-world scenarios. Although unidentifiable, we show that, like the tree-structured graphs, the ambiguity is limited to an equivalence class. This limited ambiguity can help provide meaningful clustering information (even with noise), which is helpful in computer and social networks, protein-protein interaction networks, and power networks. Furthermore, we devise an algorithm based on a novel ancestral testing method for recovering the equivalence class. We complement these results with finite sample guarantees for the algorithm in the high-dimensional regime.

The Saddle-Point Accountant for Differential Privacy

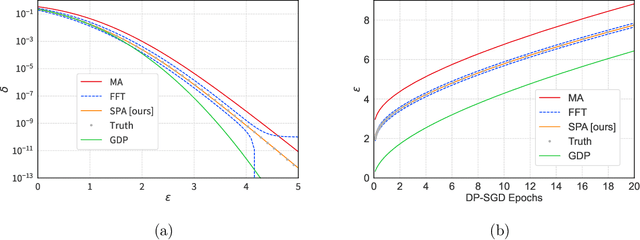
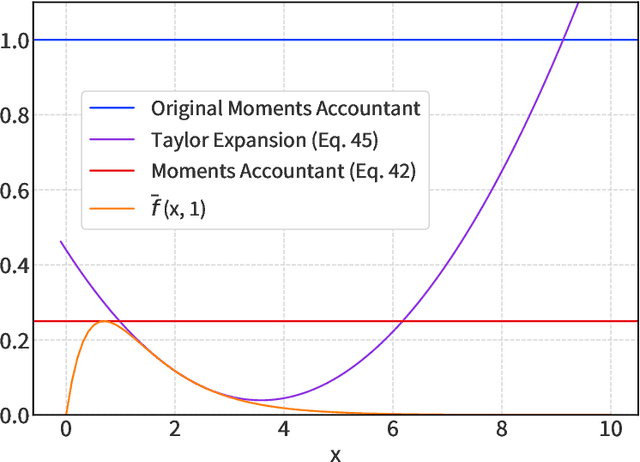
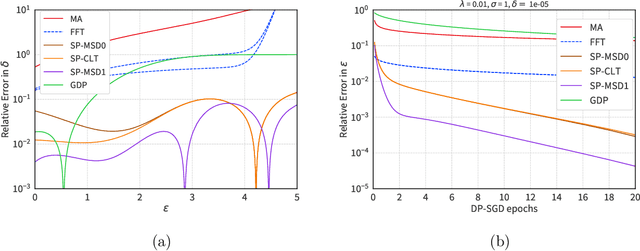
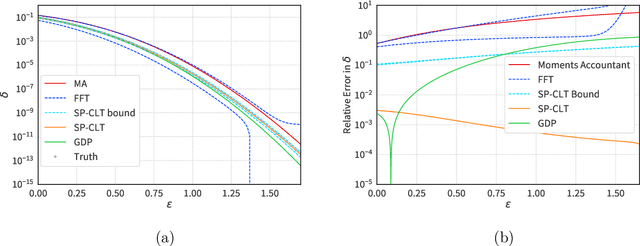
We introduce a new differential privacy (DP) accountant called the saddle-point accountant (SPA). SPA approximates privacy guarantees for the composition of DP mechanisms in an accurate and fast manner. Our approach is inspired by the saddle-point method -- a ubiquitous numerical technique in statistics. We prove rigorous performance guarantees by deriving upper and lower bounds for the approximation error offered by SPA. The crux of SPA is a combination of large-deviation methods with central limit theorems, which we derive via exponentially tilting the privacy loss random variables corresponding to the DP mechanisms. One key advantage of SPA is that it runs in constant time for the $n$-fold composition of a privacy mechanism. Numerical experiments demonstrate that SPA achieves comparable accuracy to state-of-the-art accounting methods with a faster runtime.

Cactus Mechanisms: Optimal Differential Privacy Mechanisms in the Large-Composition Regime

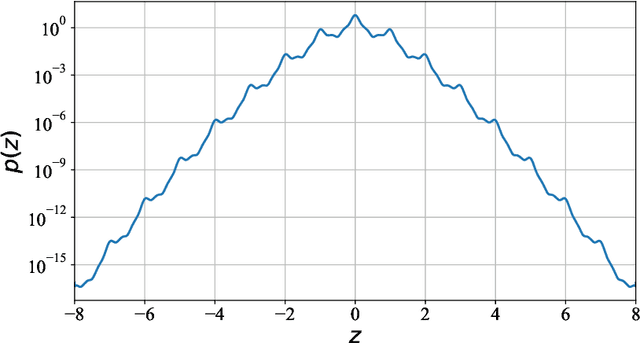
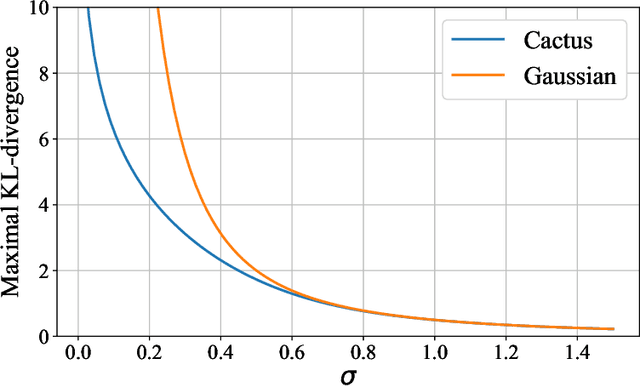
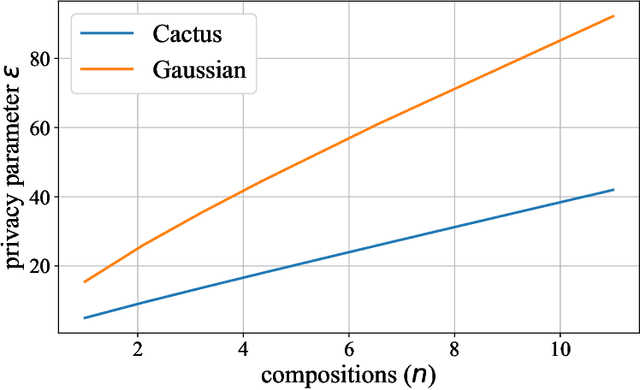
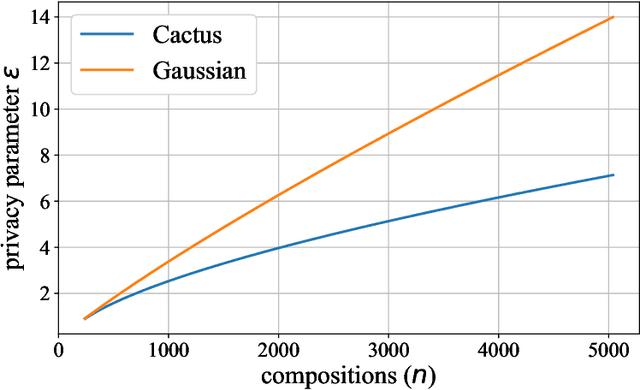
Most differential privacy mechanisms are applied (i.e., composed) numerous times on sensitive data. We study the design of optimal differential privacy mechanisms in the limit of a large number of compositions. As a consequence of the law of large numbers, in this regime the best privacy mechanism is the one that minimizes the Kullback-Leibler divergence between the conditional output distributions of the mechanism given two different inputs. We formulate an optimization problem to minimize this divergence subject to a cost constraint on the noise. We first prove that additive mechanisms are optimal. Since the optimization problem is infinite dimensional, it cannot be solved directly; nevertheless, we quantize the problem to derive near-optimal additive mechanisms that we call "cactus mechanisms" due to their shape. We show that our quantization approach can be arbitrarily close to an optimal mechanism. Surprisingly, for quadratic cost, the Gaussian mechanism is strictly sub-optimal compared to this cactus mechanism. Finally, we provide numerical results which indicate that cactus mechanism outperforms the Gaussian mechanism for a finite number of compositions.

A Machine Learning Framework for Event Identification via Modal Analysis of PMU Data

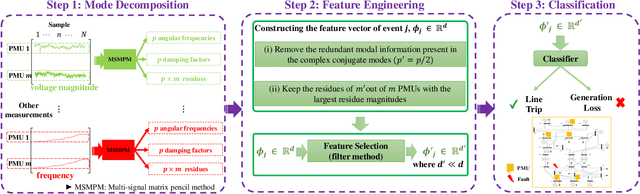
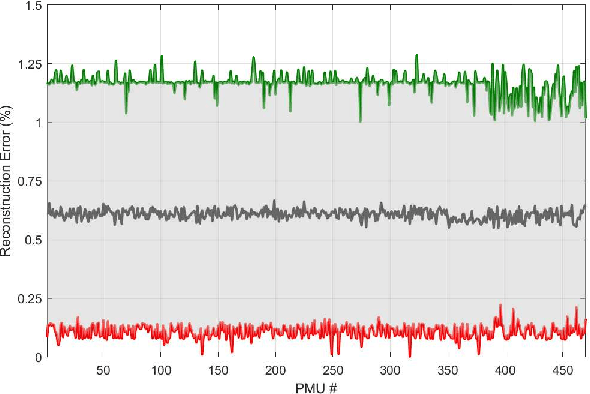
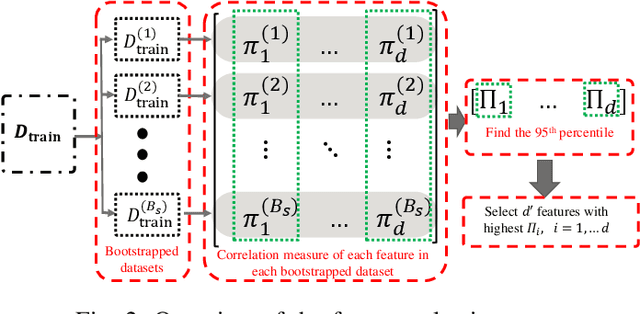
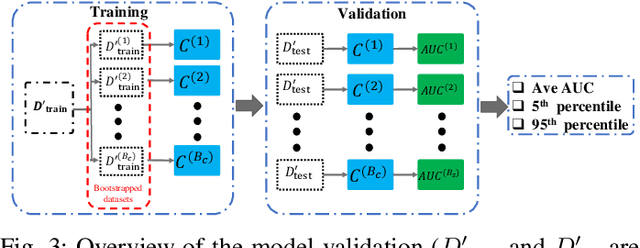
Power systems are prone to a variety of events (e.g. line trips and generation loss) and real-time identification of such events is crucial in terms of situational awareness, reliability, and security. Using measurements from multiple synchrophasors, i.e., phasor measurement units (PMUs), we propose to identify events by extracting features based on modal dynamics. We combine such traditional physics-based feature extraction methods with machine learning to distinguish different event types. Including all measurement channels at each PMU allows exploiting diverse features but also requires learning classification models over a high-dimensional space. To address this issue, various feature selection methods are implemented to choose the best subset of features. Using the obtained subset of features, we investigate the performance of two well-known classification models, namely, logistic regression (LR) and support vector machines (SVM) to identify generation loss and line trip events in two datasets. The first dataset is obtained from simulated generation loss and line trip events in the Texas 2000-bus synthetic grid. The second is a proprietary dataset with labeled events obtained from a large utility in the USA involving measurements from nearly 500 PMUs. Our results indicate that the proposed framework is promising for identifying the two types of events.

Three Variants of Differential Privacy: Lossless Conversion and Applications

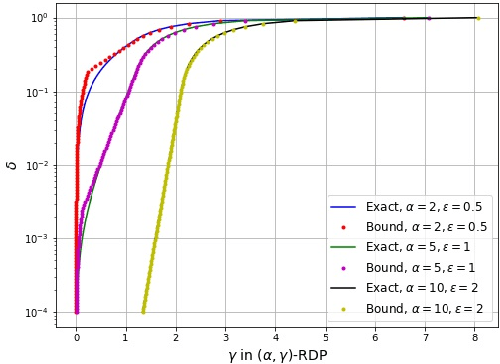
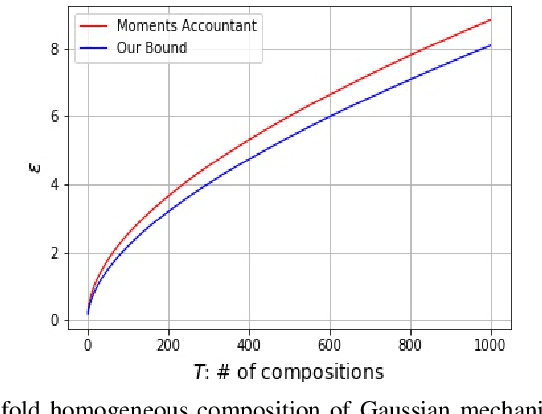
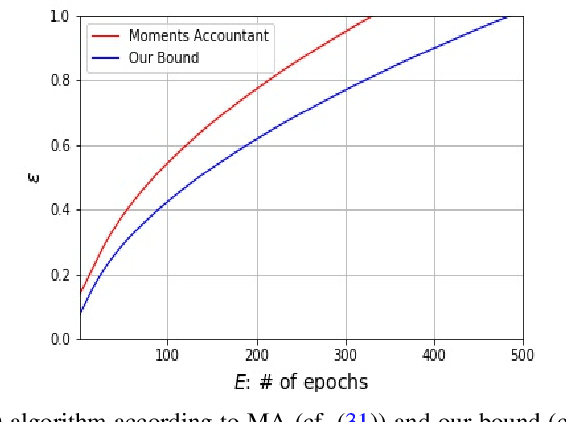
We consider three different variants of differential privacy (DP), namely approximate DP, R\'enyi DP (RDP), and hypothesis test DP. In the first part, we develop a machinery for optimally relating approximate DP to RDP based on the joint range of two $f$-divergences that underlie the approximate DP and RDP. In particular, this enables us to derive the optimal approximate DP parameters of a mechanism that satisfies a given level of RDP. As an application, we apply our result to the moments accountant framework for characterizing privacy guarantees of noisy stochastic gradient descent (SGD). When compared to the state-of-the-art, our bounds may lead to about 100 more stochastic gradient descent iterations for training deep learning models for the same privacy budget. In the second part, we establish a relationship between RDP and hypothesis test DP which allows us to translate the RDP constraint into a tradeoff between type I and type II error probabilities of a certain binary hypothesis test. We then demonstrate that for noisy SGD our result leads to tighter privacy guarantees compared to the recently proposed $f$-DP framework for some range of parameters.