Three Variants of Differential Privacy: Lossless Conversion and Applications

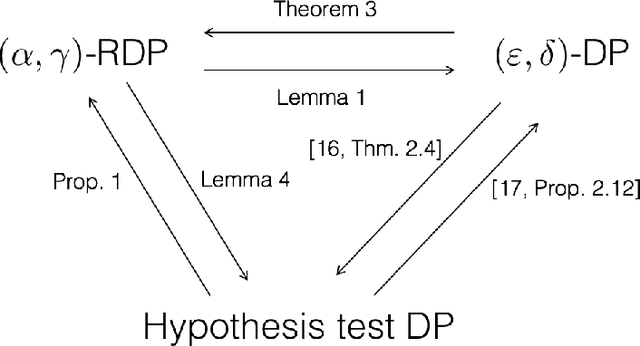
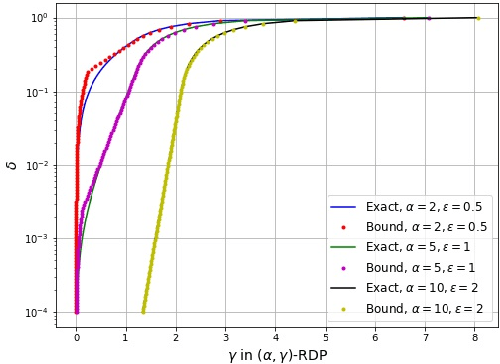
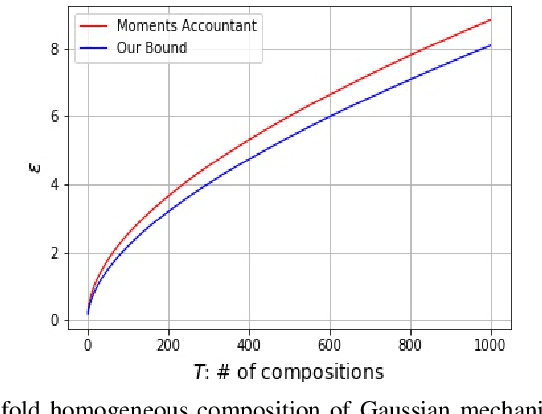
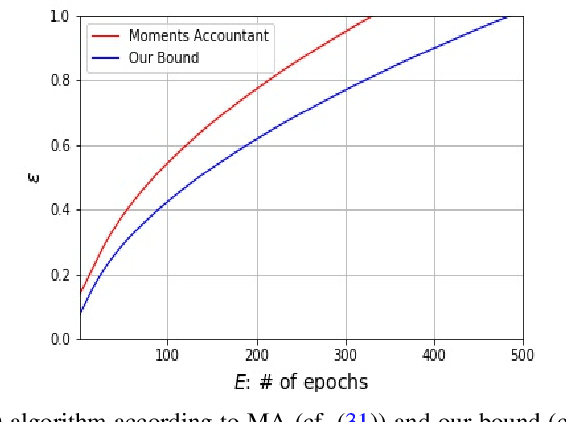
We consider three different variants of differential privacy (DP), namely approximate DP, R\'enyi DP (RDP), and hypothesis test DP. In the first part, we develop a machinery for optimally relating approximate DP to RDP based on the joint range of two $f$-divergences that underlie the approximate DP and RDP. In particular, this enables us to derive the optimal approximate DP parameters of a mechanism that satisfies a given level of RDP. As an application, we apply our result to the moments accountant framework for characterizing privacy guarantees of noisy stochastic gradient descent (SGD). When compared to the state-of-the-art, our bounds may lead to about 100 more stochastic gradient descent iterations for training deep learning models for the same privacy budget. In the second part, we establish a relationship between RDP and hypothesis test DP which allows us to translate the RDP constraint into a tradeoff between type I and type II error probabilities of a certain binary hypothesis test. We then demonstrate that for noisy SGD our result leads to tighter privacy guarantees compared to the recently proposed $f$-DP framework for some range of parameters.

A Better Bound Gives a Hundred Rounds: Enhanced Privacy Guarantees via $f$-Divergences

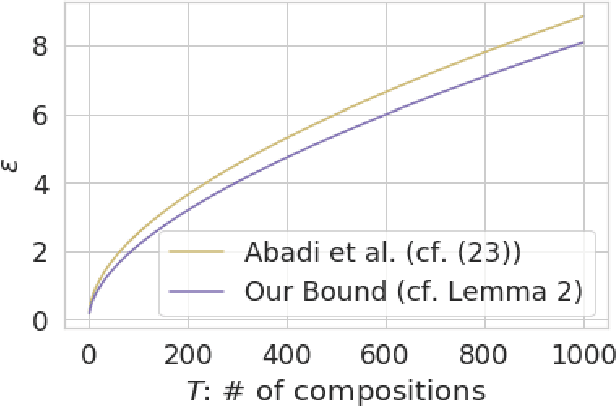
We derive the optimal differential privacy (DP) parameters of a mechanism that satisfies a given level of R\'enyi differential privacy (RDP). Our result is based on the joint range of two $f$-divergences that underlie the approximate and the R\'enyi variations of differential privacy. We apply our result to the moments accountant framework for characterizing privacy guarantees of stochastic gradient descent. When compared to the state-of-the-art, our bounds may lead to about 100 more stochastic gradient descent iterations for training deep learning models for the same privacy budget.

Theoretical Guarantees for Model Auditing with Finite Adversaries

Privacy concerns have led to the development of privacy-preserving approaches for learning models from sensitive data. Yet, in practice, even models learned with privacy guarantees can inadvertently memorize unique training examples or leak sensitive features. To identify such privacy violations, existing model auditing techniques use finite adversaries defined as machine learning models with (a) access to some finite side information (e.g., a small auditing dataset), and (b) finite capacity (e.g., a fixed neural network architecture). Our work investigates the requirements under which an unsuccessful attempt to identify privacy violations by a finite adversary implies that no stronger adversary can succeed at such a task. We do so via parameters that quantify the capabilities of the finite adversary, including the size of the neural network employed by such an adversary and the amount of side information it has access to as well as the regularity of the (perhaps privacy-guaranteeing) audited model.

Learning Generative Adversarial RePresentations (GAP) under Fairness and Censoring Constraints

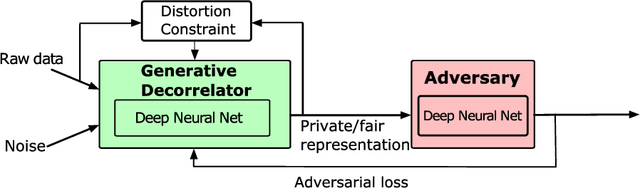
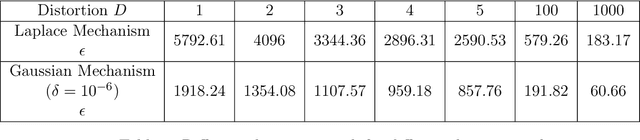
We present Generative Adversarial rePresentations (GAP) as a data-driven framework for learning censored and/or fair representations. GAP leverages recent advancements in adversarial learning to allow a data holder to learn universal representations that decouple a set of sensitive attributes from the rest of the dataset. Under GAP, finding the optimal mechanism? {decorrelating encoder/decorrelator} is formulated as a constrained minimax game between a data encoder and an adversary. We show that for appropriately chosen adversarial loss functions, GAP provides {censoring} guarantees against strong information-theoretic adversaries and enforces demographic parity. We also evaluate the performance of GAP on multi-dimensional Gaussian mixture models and real datasets, and show how a designer can certify that representations learned under an adversary with a fixed architecture perform well against more complex adversaries.