A Better Bound Gives a Hundred Rounds: Enhanced Privacy Guarantees via $f$-Divergences

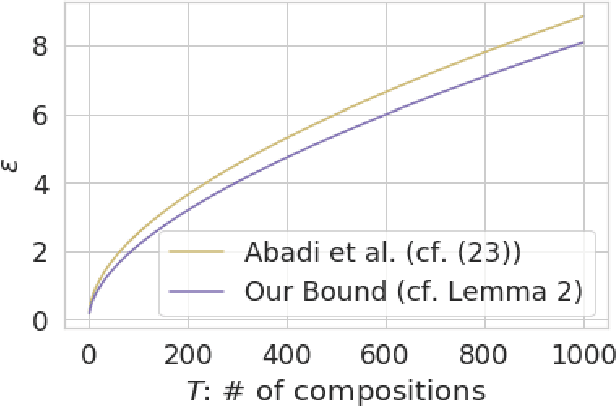
We derive the optimal differential privacy (DP) parameters of a mechanism that satisfies a given level of R\'enyi differential privacy (RDP). Our result is based on the joint range of two $f$-divergences that underlie the approximate and the R\'enyi variations of differential privacy. We apply our result to the moments accountant framework for characterizing privacy guarantees of stochastic gradient descent. When compared to the state-of-the-art, our bounds may lead to about 100 more stochastic gradient descent iterations for training deep learning models for the same privacy budget.