Locally Private Sampling with Public Data

Local differential privacy (LDP) is increasingly employed in privacy-preserving machine learning to protect user data before sharing it with an untrusted aggregator. Most LDP methods assume that users possess only a single data record, which is a significant limitation since users often gather extensive datasets (e.g., images, text, time-series data) and frequently have access to public datasets. To address this limitation, we propose a locally private sampling framework that leverages both the private and public datasets of each user. Specifically, we assume each user has two distributions: $p$ and $q$ that represent their private dataset and the public dataset, respectively. The objective is to design a mechanism that generates a private sample approximating $p$ while simultaneously preserving $q$. We frame this objective as a minimax optimization problem using $f$-divergence as the utility measure. We fully characterize the minimax optimal mechanisms for general $f$-divergences provided that $p$ and $q$ are discrete distributions. Remarkably, we demonstrate that this optimal mechanism is universal across all $f$-divergences. Experiments validate the effectiveness of our minimax optimal sampler compared to the state-of-the-art locally private sampler.

Privacy Loss of Noisy Stochastic Gradient Descent Might Converge Even for Non-Convex Losses

The Noisy-SGD algorithm is widely used for privately training machine learning models. Traditional privacy analyses of this algorithm assume that the internal state is publicly revealed, resulting in privacy loss bounds that increase indefinitely with the number of iterations. However, recent findings have shown that if the internal state remains hidden, then the privacy loss might remain bounded. Nevertheless, this remarkable result heavily relies on the assumption of (strong) convexity of the loss function. It remains an important open problem to further relax this condition while proving similar convergent upper bounds on the privacy loss. In this work, we address this problem for DP-SGD, a popular variant of Noisy-SGD that incorporates gradient clipping to limit the impact of individual samples on the training process. Our findings demonstrate that the privacy loss of projected DP-SGD converges exponentially fast, without requiring convexity or smoothness assumptions on the loss function. In addition, we analyze the privacy loss of regularized (unprojected) DP-SGD. To obtain these results, we directly analyze the hockey-stick divergence between coupled stochastic processes by relying on non-linear data processing inequalities.

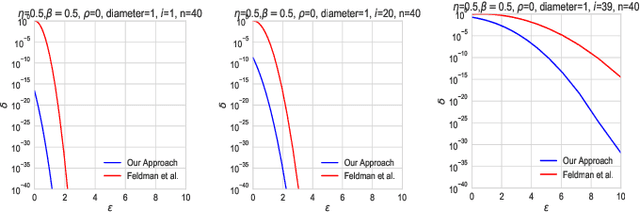
Privacy Analysis of Online Learning Algorithms via Contraction Coefficients

We propose an information-theoretic technique for analyzing privacy guarantees of online algorithms. Specifically, we demonstrate that differential privacy guarantees of iterative algorithms can be determined by a direct application of contraction coefficients derived from strong data processing inequalities for $f$-divergences. Our technique relies on generalizing the Dobrushin's contraction coefficient for total variation distance to an $f$-divergence known as $E_\gamma$-divergence. $E_\gamma$-divergence, in turn, is equivalent to approximate differential privacy. As an example, we apply our technique to derive the differential privacy parameters of gradient descent. Moreover, we also show that this framework can be tailored to batch learning algorithms that can be implemented with one pass over the training dataset.

On the alpha-loss Landscape in the Logistic Model

We analyze the optimization landscape of a recently introduced tunable class of loss functions called $\alpha$-loss, $\alpha \in (0,\infty]$, in the logistic model. This family encapsulates the exponential loss ($\alpha = 1/2$), the log-loss ($\alpha = 1$), and the 0-1 loss ($\alpha = \infty$) and contains compelling properties that enable the practitioner to discern among a host of operating conditions relevant to emerging learning methods. Specifically, we study the evolution of the optimization landscape of $\alpha$-loss with respect to $\alpha$ using tools drawn from the study of strictly-locally-quasi-convex functions in addition to geometric techniques. We interpret these results in terms of optimization complexity via normalized gradient descent.

To Split or Not to Split: The Impact of Disparate Treatment in Classification

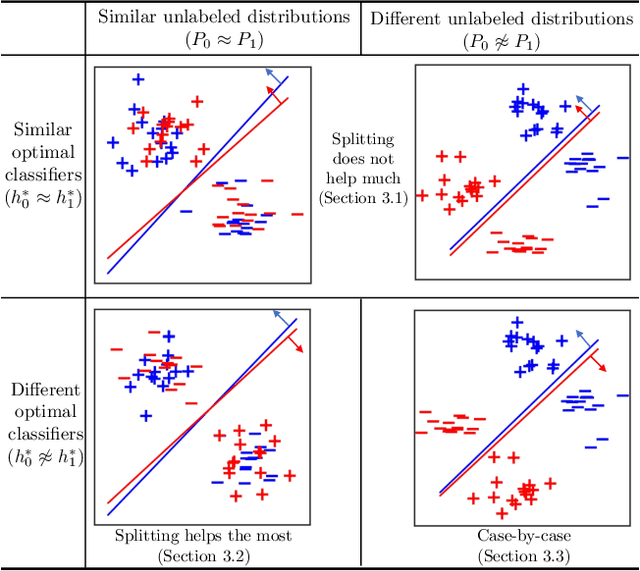
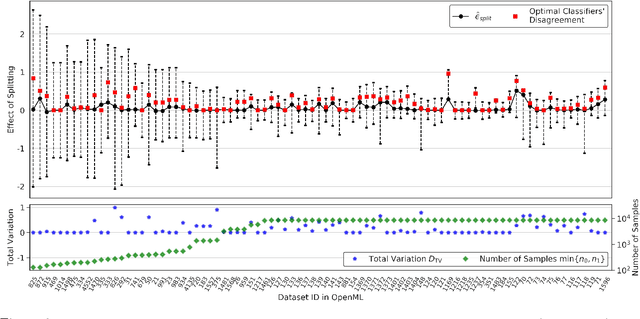
Disparate treatment occurs when a machine learning model produces different decisions for groups defined by a legally protected or sensitive attribute (e.g., race, gender). In domains where prediction accuracy is paramount, it is acceptable to fit a model which exhibits disparate treatment. We explore the effect of splitting classifiers (i.e., training and deploying a separate classifier on each group) and derive an information-theoretic impossibility result: there exists precise conditions where a group-blind classifier will always have a non-trivial performance gap from the split classifiers. We further demonstrate that, in the finite sample regime, splitting is no longer always beneficial and relies on the number of samples from each group and the complexity of the hypothesis class. We provide data-dependent bounds for understanding the effect of splitting and illustrate these bounds on real-world datasets.

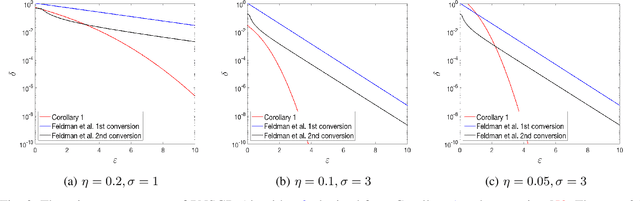
Privacy Amplification of Iterative Algorithms via Contraction Coefficients

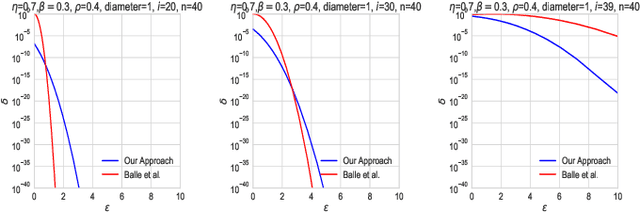
We investigate the framework of privacy amplification by iteration, recently proposed by Feldman et al., from an information-theoretic lens. We demonstrate that differential privacy guarantees of iterative mappings can be determined by a direct application of contraction coefficients derived from strong data processing inequalities for $f$-divergences. In particular, by generalizing the Dobrushin's contraction coefficient for total variation distance to an $f$-divergence known as $E_{\gamma}$-divergence, we derive tighter bounds on the differential privacy parameters of the projected noisy stochastic gradient descent algorithm with hidden intermediate updates.

Theoretical Guarantees for Model Auditing with Finite Adversaries

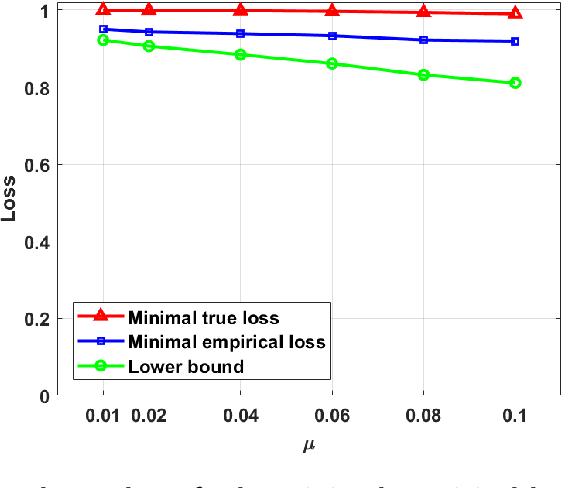
Privacy concerns have led to the development of privacy-preserving approaches for learning models from sensitive data. Yet, in practice, even models learned with privacy guarantees can inadvertently memorize unique training examples or leak sensitive features. To identify such privacy violations, existing model auditing techniques use finite adversaries defined as machine learning models with (a) access to some finite side information (e.g., a small auditing dataset), and (b) finite capacity (e.g., a fixed neural network architecture). Our work investigates the requirements under which an unsuccessful attempt to identify privacy violations by a finite adversary implies that no stronger adversary can succeed at such a task. We do so via parameters that quantify the capabilities of the finite adversary, including the size of the neural network employed by such an adversary and the amount of side information it has access to as well as the regularity of the (perhaps privacy-guaranteeing) audited model.

A Tunable Loss Function for Classification

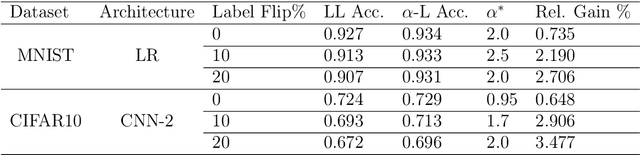
Recently, a parametrized class of loss functions called $\alpha$-loss, $\alpha \in [1,\infty]$, has been introduced for classification. This family, which includes the log-loss and the 0-1 loss as special cases, comes with compelling properties including an equivalent margin-based form which is classification-calibrated for all $\alpha$. We introduce a generalization of this family to the entire range of $\alpha \in (0,\infty]$ and establish how the parameter $\alpha$ enables the practitioner to choose among a host of operating conditions that are important in modern machine learning tasks. We prove that smaller $\alpha$ values are more conducive to faster optimization; in fact, $\alpha$-loss is convex for $\alpha \le 1$ and quasi-convex for $\alpha >1$. Moreover, we establish bounds to quantify the degradation of the local-quasi-convexity of the optimization landscape as $\alpha$ increases; we show that this directly translates to a computational slow down. On the other hand, our theoretical results also suggest that larger $\alpha$ values lead to better generalization performance. This is a consequence of the ability of the $\alpha$-loss to limit the effect of less likely data as $\alpha$ increases from 1, thereby facilitating robustness to outliers and noise in the training data. We provide strong evidence supporting this assertion with several experiments on benchmark datasets that establish the efficacy of $\alpha$-loss for $\alpha > 1$ in robustness to errors in the training data. Of equal interest is the fact that, for $\alpha < 1$, our experiments show that the decreased robustness seems to counteract class imbalances in training data.

A Tunable Loss Function for Binary Classification

We present $\alpha$-loss, $\alpha \in [1,\infty]$, a tunable loss function for binary classification that bridges log-loss ($\alpha=1$) and $0$-$1$ loss ($\alpha = \infty$). We prove that $\alpha$-loss has an equivalent margin-based form and is classification-calibrated, two desirable properties for a good surrogate loss function for the ideal yet intractable $0$-$1$ loss. For logistic regression-based classification, we provide an upper bound on the difference between the empirical and expected risk at the empirical risk minimizers for $\alpha$-loss by exploiting its Lipschitzianity along with recent results on the landscape features of empirical risk functions. Finally, we show that $\alpha$-loss with $\alpha = 2$ performs better than log-loss on MNIST for logistic regression.

Information Extraction Under Privacy Constraints

A privacy-constrained information extraction problem is considered where for a pair of correlated discrete random variables $(X,Y)$ governed by a given joint distribution, an agent observes $Y$ and wants to convey to a potentially public user as much information about $Y$ as possible without compromising the amount of information revealed about $X$. To this end, the so-called {\em rate-privacy function} is introduced to quantify the maximal amount of information (measured in terms of mutual information) that can be extracted from $Y$ under a privacy constraint between $X$ and the extracted information, where privacy is measured using either mutual information or maximal correlation. Properties of the rate-privacy function are analyzed and information-theoretic and estimation-theoretic interpretations of it are presented for both the mutual information and maximal correlation privacy measures. It is also shown that the rate-privacy function admits a closed-form expression for a large family of joint distributions of $(X,Y)$. Finally, the rate-privacy function under the mutual information privacy measure is considered for the case where $(X,Y)$ has a joint probability density function by studying the problem where the extracted information is a uniform quantization of $Y$ corrupted by additive Gaussian noise. The asymptotic behavior of the rate-privacy function is studied as the quantization resolution grows without bound and it is observed that not all of the properties of the rate-privacy function carry over from the discrete to the continuous case.