Privacy Amplification of Iterative Algorithms via Contraction Coefficients
Paper and Code
Jan 17, 2020
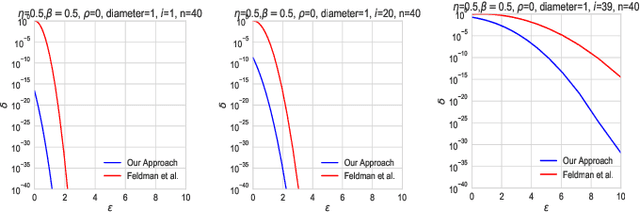
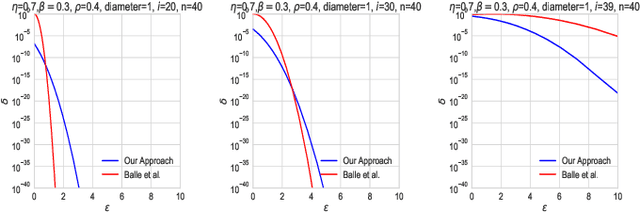
We investigate the framework of privacy amplification by iteration, recently proposed by Feldman et al., from an information-theoretic lens. We demonstrate that differential privacy guarantees of iterative mappings can be determined by a direct application of contraction coefficients derived from strong data processing inequalities for $f$-divergences. In particular, by generalizing the Dobrushin's contraction coefficient for total variation distance to an $f$-divergence known as $E_{\gamma}$-divergence, we derive tighter bounds on the differential privacy parameters of the projected noisy stochastic gradient descent algorithm with hidden intermediate updates.
* Submitted for publication
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge