Locally Private Sampling with Public Data

Local differential privacy (LDP) is increasingly employed in privacy-preserving machine learning to protect user data before sharing it with an untrusted aggregator. Most LDP methods assume that users possess only a single data record, which is a significant limitation since users often gather extensive datasets (e.g., images, text, time-series data) and frequently have access to public datasets. To address this limitation, we propose a locally private sampling framework that leverages both the private and public datasets of each user. Specifically, we assume each user has two distributions: $p$ and $q$ that represent their private dataset and the public dataset, respectively. The objective is to design a mechanism that generates a private sample approximating $p$ while simultaneously preserving $q$. We frame this objective as a minimax optimization problem using $f$-divergence as the utility measure. We fully characterize the minimax optimal mechanisms for general $f$-divergences provided that $p$ and $q$ are discrete distributions. Remarkably, we demonstrate that this optimal mechanism is universal across all $f$-divergences. Experiments validate the effectiveness of our minimax optimal sampler compared to the state-of-the-art locally private sampler.

Machine Learning-powered Course Allocation

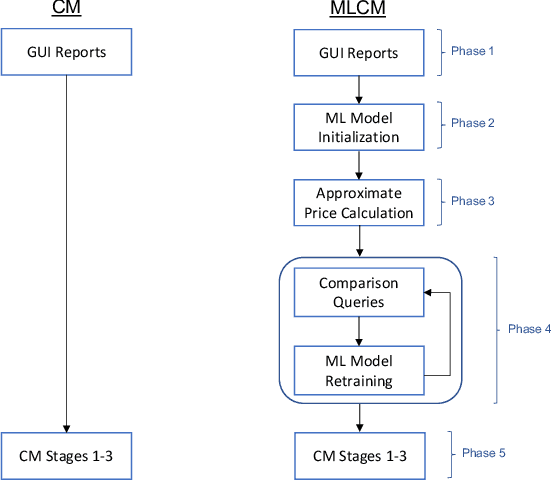
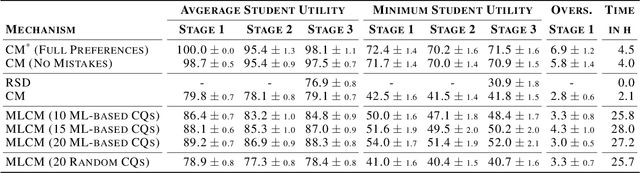
We introduce a machine learning-powered course allocation mechanism. Concretely, we extend the state-of-the-art Course Match mechanism with a machine learning-based preference elicitation module. In an iterative, asynchronous manner, this module generates pairwise comparison queries that are tailored to each individual student. Regarding incentives, our machine learning-powered course match (MLCM) mechanism retains the attractive strategyproofness in the large property of Course Match. Regarding welfare, we perform computational experiments using a simulator that was fitted to real-world data. We find that, compared to Course Match, MLCM is able to increase average student utility by 4%-9% and minimum student utility by 10%-21%, even with only ten comparison queries.

Piecewise-Linear Activations or Analytic Activation Functions: Which Produce More Expressive Neural Networks?

Many currently available universal approximation theorems affirm that deep feedforward networks defined using any suitable activation function can approximate any integrable function locally in $L^1$-norm. Though different approximation rates are available for deep neural networks defined using other classes of activation functions, there is little explanation for the empirically confirmed advantage that ReLU networks exhibit over their classical (e.g. sigmoidal) counterparts. Our main result demonstrates that deep networks with piecewise linear activation (e.g. ReLU or PReLU) are fundamentally more expressive than deep feedforward networks with analytic (e.g. sigmoid, Swish, GeLU, or Softplus). More specifically, we construct a strict refinement of the topology on the space $L^1_{\operatorname{loc}}(\mathbb{R}^d,\mathbb{R}^D)$ of locally Lebesgue-integrable functions, in which the set of deep ReLU networks with (bilinear) pooling $\operatorname{NN}^{\operatorname{ReLU} + \operatorname{Pool}}$ is dense (i.e. universal) but the set of deep feedforward networks defined using any combination of analytic activation functions with (or without) pooling layers $\operatorname{NN}^{\omega+\operatorname{Pool}}$ is not dense (i.e. not universal). Our main result is further explained by \textit{quantitatively} demonstrating that this "separation phenomenon" between the networks in $\operatorname{NN}^{\operatorname{ReLU}+\operatorname{Pool}}$ and those in $\operatorname{NN}^{\omega+\operatorname{Pool}}$ by showing that the networks in $\operatorname{NN}^{\operatorname{ReLU}}$ are capable of approximate any compactly supported Lipschitz function while \textit{simultaneously} approximating its essential support; whereas, the networks in $\operatorname{NN}^{\omega+\operatorname{pool}}$ cannot.

Universal Approximation Under Constraints is Possible with Transformers

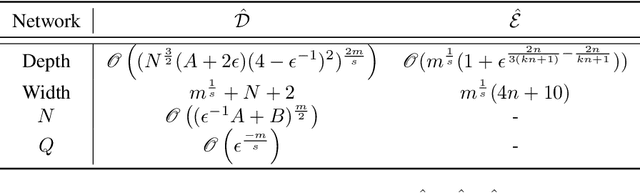
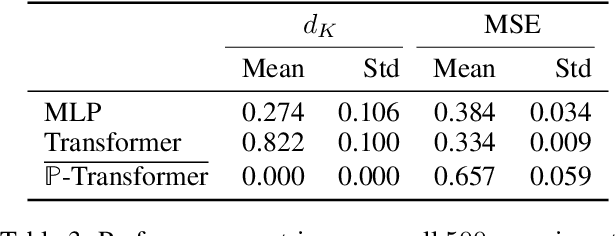
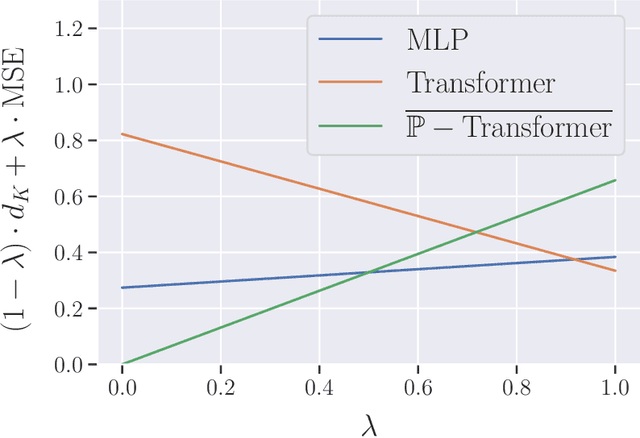
Many practical problems need the output of a machine learning model to satisfy a set of constraints, $K$. Nevertheless, there is no known guarantee that classical neural network architectures can exactly encode constraints while simultaneously achieving universality. We provide a quantitative constrained universal approximation theorem which guarantees that for any non-convex compact set $K$ and any continuous function $f:\mathbb{R}^n\rightarrow K$, there is a probabilistic transformer $\hat{F}$ whose randomized outputs all lie in $K$ and whose expected output uniformly approximates $f$. Our second main result is a "deep neural version" of Berge's Maximum Theorem (1963). The result guarantees that given an objective function $L$, a constraint set $K$, and a family of soft constraint sets, there is a probabilistic transformer $\hat{F}$ that approximately minimizes $L$ and whose outputs belong to $K$; moreover, $\hat{F}$ approximately satisfies the soft constraints. Our results imply the first universal approximation theorem for classical transformers with exact convex constraint satisfaction. They also yield that a chart-free universal approximation theorem for Riemannian manifold-valued functions subject to suitable geodesically convex constraints.

Overcoming The Limitations of Neural Networks in Composite-Pattern Learning with Architopes

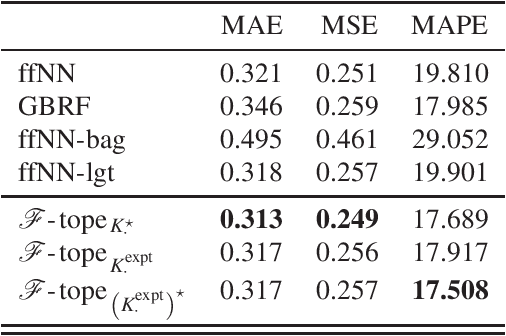
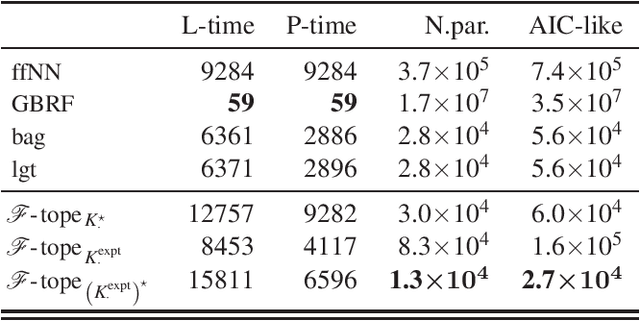
The effectiveness of neural networks in solving complex problems is well recognized; however, little is known about their limitations. We demonstrate that the feed-forward architecture, for most commonly used activation functions, is incapable of approximating functions comprised of multiple sub-patterns while simultaneously respecting their composite-pattern structure. We overcome this bottleneck with a simple architecture modification that reallocates the neurons of any single feed-forward network across several smaller sub-networks, each specialized on a distinct part of the input-space. The modified architecture, called an Architope, is more expressive on two fronts. First, it is dense in an associated space of piecewise continuous functions in which the feed-forward architecture is not dense. Second, it achieves the same approximation rate as the feed-forward networks while only requiring $\mathscr{O}(N^{-1})$ fewer parameters in its hidden layers. Moreover, the architecture achieves these approximation improvements while preserving the target's composite-pattern structure.

Architopes: An Architecture Modification for Composite Pattern Learning, Increased Expressiveness, and Reduced Training Time

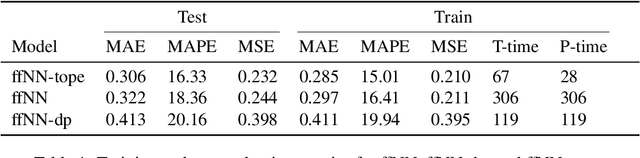
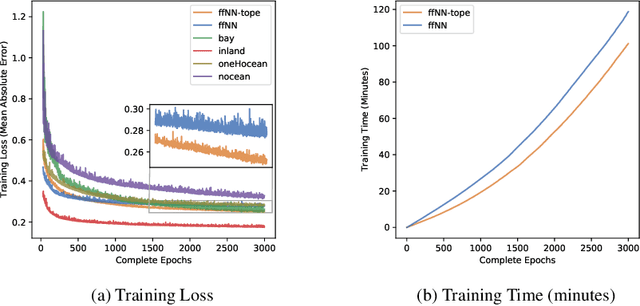
We introduce a simple neural network architecture modification that enables composite pattern learning, increases expressiveness, and reduces training time. This expressibility improvement is explained by the density of the modified architecture in a new refined local $L^p$-space describing composite patterns. In contrast, most feed-forward neural network architectures with sigmoid activation functions are shown not to be dense in this space. In practice, restrictions have to be placed on the dimension of any architecture's parameter space. $L^1$ approximation bounds are obtained in terms of the number of the trainable parameters. Likewise, convergence guarantees are obtained as the imposed restrictions are asymptotically removed. By exploiting the new architecture's structure, a parallelizable training meta-algorithm is provided, and numerical evaluations are made using the California housing dataset.