Prices, Bids, Values: Everything, Everywhere, All at Once

We study the design of iterative combinatorial auctions (ICAs). The main challenge in this domain is that the bundle space grows exponentially in the number of items. To address this, several papers have recently proposed machine learning (ML)-based preference elicitation algorithms that aim to elicit only the most important information from bidders to maximize efficiency. The SOTA ML-based algorithms elicit bidders' preferences via value queries (i.e., "What is your value for the bundle $\{A,B\}$?"). However, the most popular iterative combinatorial auction in practice elicits information via more practical \emph{demand queries} (i.e., "At prices $p$, what is your most preferred bundle of items?"). In this paper, we examine the advantages of value and demand queries from both an auction design and an ML perspective. We propose a novel ML algorithm that provably integrates the full information from both query types. As suggested by our theoretical analysis, our experimental results verify that combining demand and value queries results in significantly better learning performance. Building on these insights, we present MLHCA, the most efficient ICA ever designed. MLHCA substantially outperforms the previous SOTA in realistic auction settings, delivering large efficiency gains. Compared to the previous SOTA, MLHCA reduces efficiency loss by up to a factor of 10, and in the most challenging and realistic domain, MLHCA outperforms the previous SOTA using 30% fewer queries. Thus, MLHCA achieves efficiency improvements that translate to welfare gains of hundreds of millions of USD, while also reducing the cognitive load on the bidders, establishing a new benchmark both for practicability and for economic impact.

Truthful Aggregation of LLMs with an Application to Online Advertising

We address the challenge of aggregating the preferences of multiple agents over LLM-generated replies to user queries, where agents might modify or exaggerate their preferences. New agents may participate for each new query, making fine-tuning LLMs on these preferences impractical. To overcome these challenges, we propose an auction mechanism that operates without fine-tuning or access to model weights. This mechanism is designed to provably converge to the ouput of the optimally fine-tuned LLM as computational resources are increased. The mechanism can also incorporate contextual information about the agents when avaiable, which significantly accelerates its convergence. A well-designed payment rule ensures that truthful reporting is the optimal strategy for all agents, while also promoting an equity property by aligning each agent's utility with her contribution to social welfare - an essential feature for the mechanism's long-term viability. While our approach can be applied whenever monetary transactions are permissible, our flagship application is in online advertising. In this context, advertisers try to steer LLM-generated responses towards their brand interests, while the platform aims to maximize advertiser value and ensure user satisfaction. Experimental results confirm that our mechanism not only converges efficiently to the optimally fine-tuned LLM but also significantly boosts advertiser value and platform revenue, all with minimal computational overhead.

Scalable Mechanism Design for Multi-Agent Path Finding

Multi-Agent Path Finding (MAPF) involves determining paths for multiple agents to travel simultaneously through a shared area toward particular goal locations. This problem is computationally complex, especially when dealing with large numbers of agents, as is common in realistic applications like autonomous vehicle coordination. Finding an optimal solution is often computationally infeasible, making the use of approximate algorithms essential. Adding to the complexity, agents might act in a self-interested and strategic way, possibly misrepresenting their goals to the MAPF algorithm if it benefits them. Although the field of mechanism design offers tools to align incentives, using these tools without careful consideration can fail when only having access to approximately optimal outcomes. Since approximations are crucial for scalable MAPF algorithms, this poses a significant challenge. In this work, we introduce the problem of scalable mechanism design for MAPF and propose three strategyproof mechanisms, two of which even use approximate MAPF algorithms. We test our mechanisms on realistic MAPF domains with problem sizes ranging from dozens to hundreds of agents. Our findings indicate that they improve welfare beyond a simple baseline.

Machine Learning-powered Combinatorial Clock Auction

We study the design of iterative combinatorial auctions (ICAs). The main challenge in this domain is that the bundle space grows exponentially in the number of items. To address this, several papers have recently proposed machine learning (ML)-based preference elicitation algorithms that aim to elicit only the most important information from bidders. However, from a practical point of view, the main shortcoming of this prior work is that those designs elicit bidders' preferences via value queries (i.e., ``What is your value for the bundle $\{A,B\}$?''). In most real-world ICA domains, value queries are considered impractical, since they impose an unrealistically high cognitive burden on bidders, which is why they are not used in practice. In this paper, we address this shortcoming by designing an ML-powered combinatorial clock auction that elicits information from the bidders only via demand queries (i.e., ``At prices $p$, what is your most preferred bundle of items?''). We make two key technical contributions: First, we present a novel method for training an ML model on demand queries. Second, based on those trained ML models, we introduce an efficient method for determining the demand query with the highest clearing potential, for which we also provide a theoretical foundation. We experimentally evaluate our ML-based demand query mechanism in several spectrum auction domains and compare it against the most established real-world ICA: the combinatorial clock auction (CCA). Our mechanism significantly outperforms the CCA in terms of efficiency in all domains, it achieves higher efficiency in a significantly reduced number of rounds, and, using linear prices, it exhibits vastly higher clearing potential. Thus, with this paper we bridge the gap between research and practice and propose the first practical ML-powered ICA.

Machine Learning-powered Course Allocation

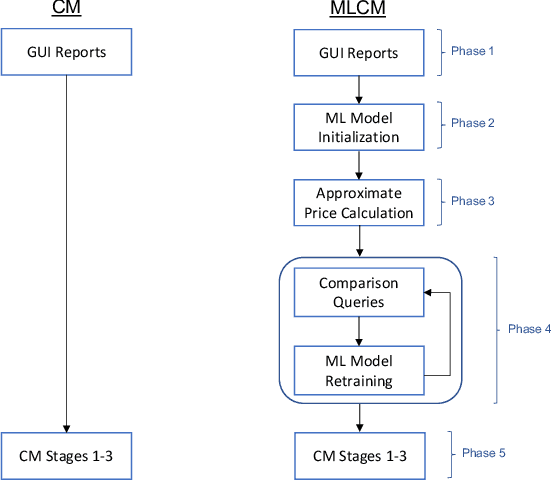
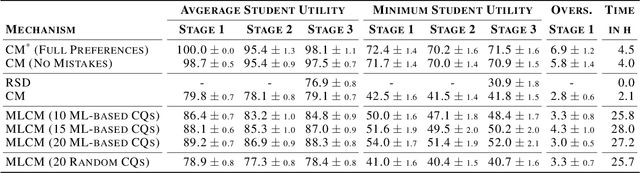
We introduce a machine learning-powered course allocation mechanism. Concretely, we extend the state-of-the-art Course Match mechanism with a machine learning-based preference elicitation module. In an iterative, asynchronous manner, this module generates pairwise comparison queries that are tailored to each individual student. Regarding incentives, our machine learning-powered course match (MLCM) mechanism retains the attractive strategyproofness in the large property of Course Match. Regarding welfare, we perform computational experiments using a simulator that was fitted to real-world data. We find that, compared to Course Match, MLCM is able to increase average student utility by 4%-9% and minimum student utility by 10%-21%, even with only ten comparison queries.

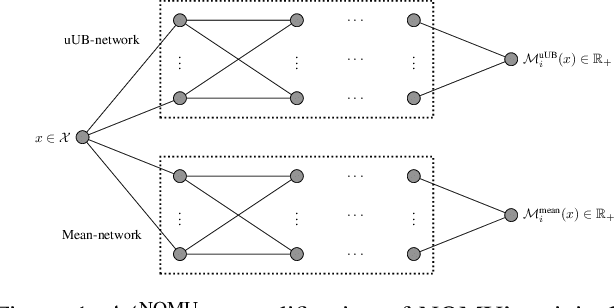
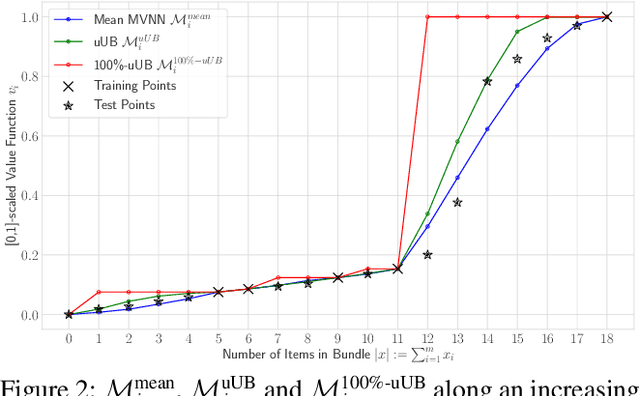
Bayesian Optimization-based Combinatorial Assignment

We study the combinatorial assignment domain, which includes combinatorial auctions and course allocation. The main challenge in this domain is that the bundle space grows exponentially in the number of items. To address this, several papers have recently proposed machine learning-based preference elicitation algorithms that aim to elicit only the most important information from agents. However, the main shortcoming of this prior work is that it does not model a mechanism's uncertainty over values for not yet elicited bundles. In this paper, we address this shortcoming by presenting a Bayesian Optimization-based Combinatorial Assignment (BOCA) mechanism. Our key technical contribution is to integrate a method for capturing model uncertainty into an iterative combinatorial auction mechanism. Concretely, we design a new method for estimating an upper uncertainty bound that can be used as an acquisition function to determine the next query to the agents. This enables the mechanism to properly explore (and not just exploit) the bundle space during its preference elicitation phase. We run computational experiments in several spectrum auction domains to evaluate BOCA's performance. Our results show that BOCA achieves higher allocative efficiency than state-of-the-art approaches.

NOMU: Neural Optimization-based Model Uncertainty

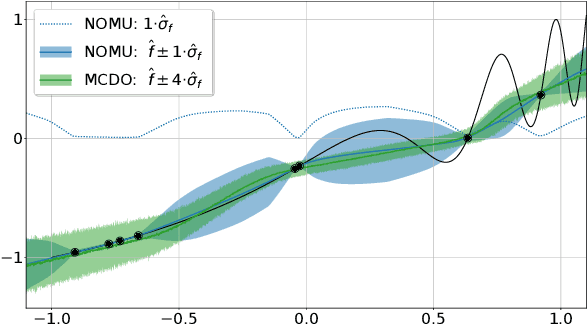
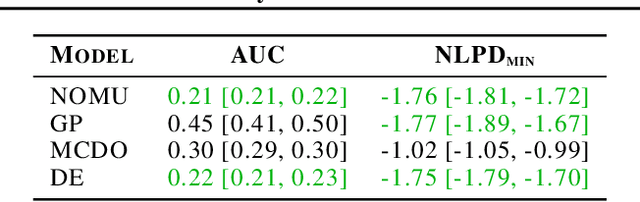
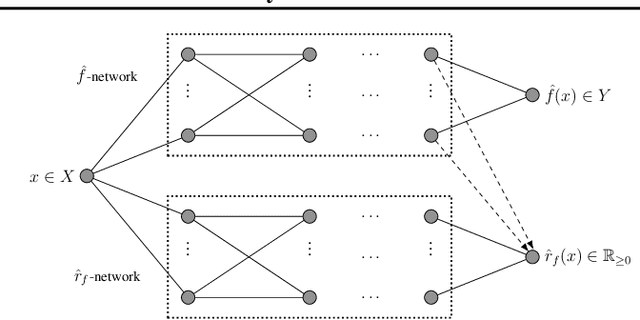
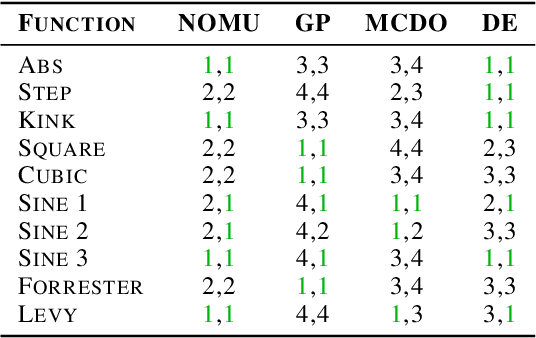
We introduce a new approach for capturing model uncertainty for neural networks (NNs) in regression, which we call Neural Optimization-based Model Uncertainty (NOMU). The main idea of NOMU is to design a network architecture consisting of two connected sub-networks, one for the model prediction and one for the model uncertainty, and to train it using a carefully designed loss function. With this design, NOMU can provide model uncertainty for any given (previously trained) NN by plugging it into the framework as the sub-network used for model prediction. NOMU is designed to yield uncertainty bounds (UBs) that satisfy four important desiderata regarding model uncertainty, which established methods often do not satisfy. Furthermore, our UBs are themselves representable as a single NN, which leads to computational cost advantages in applications such as Bayesian optimization. We evaluate NOMU experimentally in multiple settings. For regression, we show that NOMU performs as well as or better than established benchmarks. For Bayesian optimization, we show that NOMU outperforms all other benchmarks.

Improved Memory-Bounded Dynamic Programming for Decentralized POMDPs

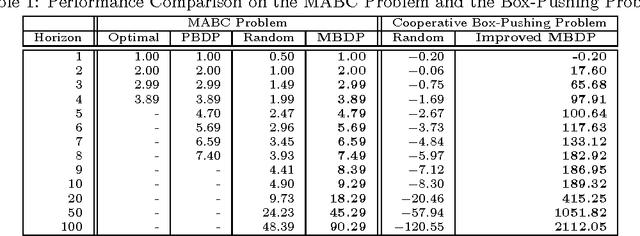
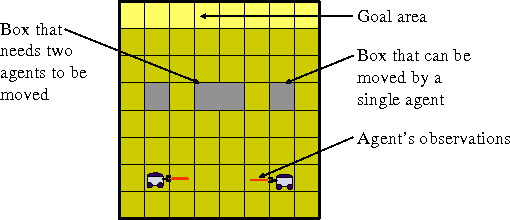
Memory-Bounded Dynamic Programming (MBDP) has proved extremely effective in solving decentralized POMDPs with large horizons. We generalize the algorithm and improve its scalability by reducing the complexity with respect to the number of observations from exponential to polynomial. We derive error bounds on solution quality with respect to this new approximation and analyze the convergence behavior. To evaluate the effectiveness of the improvements, we introduce a new, larger benchmark problem. Experimental results show that despite the high complexity of decentralized POMDPs, scalable solution techniques such as MBDP perform surprisingly well.