Josef Teichmann
Department of Mathematics, ETH Zürich, Switzerland
Signature Reconstruction from Randomized Signatures
Feb 05, 2025



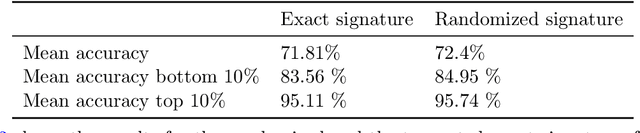
Abstract:Controlled ordinary differential equations driven by continuous bounded variation curves can be considered a continuous time analogue of recurrent neural networks for the construction of expressive features of the input curves. We ask up to which extent well known signature features of such curves can be reconstructed from controlled ordinary differential equations with (untrained) random vector fields. The answer turns out to be algebraically involved, but essentially the number of signature features, which can be reconstructed from the non-linear flow of the controlled ordinary differential equation, is exponential in its hidden dimension, when the vector fields are chosen to be neural with depth two. Moreover, we characterize a general linear independence condition on arbitrary vector fields, under which the signature features up to some fixed order can always be reconstructed. Algebraically speaking this complements in a quantitative manner several well known results from the theory of Lie algebras of vector fields and puts them in a context of machine learning.
Learning Chaotic Systems and Long-Term Predictions with Neural Jump ODEs
Jul 26, 2024



Abstract:The Path-dependent Neural Jump ODE (PD-NJ-ODE) is a model for online prediction of generic (possibly non-Markovian) stochastic processes with irregular (in time) and potentially incomplete (with respect to coordinates) observations. It is a model for which convergence to the $L^2$-optimal predictor, which is given by the conditional expectation, is established theoretically. Thereby, the training of the model is solely based on a dataset of realizations of the underlying stochastic process, without the need of knowledge of the law of the process. In the case where the underlying process is deterministic, the conditional expectation coincides with the process itself. Therefore, this framework can equivalently be used to learn the dynamics of ODE or PDE systems solely from realizations of the dynamical system with different initial conditions. We showcase the potential of our method by applying it to the chaotic system of a double pendulum. When training the standard PD-NJ-ODE method, we see that the prediction starts to diverge from the true path after about half of the evaluation time. In this work we enhance the model with two novel ideas, which independently of each other improve the performance of our modelling setup. The resulting dynamics match the true dynamics of the chaotic system very closely. The same enhancements can be used to provably enable the PD-NJ-ODE to learn long-term predictions for general stochastic datasets, where the standard model fails. This is verified in several experiments.
Robust Utility Optimization via a GAN Approach
Mar 22, 2024



Abstract:Robust utility optimization enables an investor to deal with market uncertainty in a structured way, with the goal of maximizing the worst-case outcome. In this work, we propose a generative adversarial network (GAN) approach to (approximately) solve robust utility optimization problems in general and realistic settings. In particular, we model both the investor and the market by neural networks (NN) and train them in a mini-max zero-sum game. This approach is applicable for any continuous utility function and in realistic market settings with trading costs, where only observable information of the market can be used. A large empirical study shows the versatile usability of our method. Whenever an optimal reference strategy is available, our method performs on par with it and in the (many) settings without known optimal strategy, our method outperforms all other reference strategies. Moreover, we can conclude from our study that the trained path-dependent strategies do not outperform Markovian ones. Lastly, we uncover that our generative approach for learning optimal, (non-) robust investments under trading costs generates universally applicable alternatives to well known asymptotic strategies of idealized settings.
Randomized Signature Methods in Optimal Portfolio Selection
Dec 27, 2023Abstract:We present convincing empirical results on the application of Randomized Signature Methods for non-linear, non-parametric drift estimation for a multi-variate financial market. Even though drift estimation is notoriously ill defined due to small signal to noise ratio, one can still try to learn optimal non-linear maps from data to future returns for the purposes of portfolio optimization. Randomized Signatures, in contrast to classical signatures, allow for high dimensional market dimension and provide features on the same scale. We do not contribute to the theory of Randomized Signatures here, but rather present our empirical findings on portfolio selection in real world settings including real market data and transaction costs.
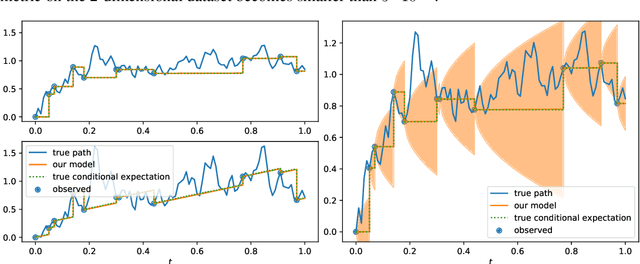
Extending Path-Dependent NJ-ODEs to Noisy Observations and a Dependent Observation Framework
Jul 24, 2023

Abstract:The Path-Dependent Neural Jump ODE (PD-NJ-ODE) is a model for predicting continuous-time stochastic processes with irregular and incomplete observations. In particular, the method learns optimal forecasts given irregularly sampled time series of incomplete past observations. So far the process itself and the coordinate-wise observation times were assumed to be independent and observations were assumed to be noiseless. In this work we discuss two extensions to lift these restrictions and provide theoretical guarantees as well as empirical examples for them.
Global universal approximation of functional input maps on weighted spaces
Jun 05, 2023Abstract:We introduce so-called functional input neural networks defined on a possibly infinite dimensional weighted space with values also in a possibly infinite dimensional output space. To this end, we use an additive family as hidden layer maps and a non-linear activation function applied to each hidden layer. Relying on Stone-Weierstrass theorems on weighted spaces, we can prove a global universal approximation result for generalizations of continuous functions going beyond the usual approximation on compact sets. This then applies in particular to approximation of (non-anticipative) path space functionals via functional input neural networks. As a further application of the weighted Stone-Weierstrass theorem we prove a global universal approximation result for linear functions of the signature. We also introduce the viewpoint of Gaussian process regression in this setting and show that the reproducing kernel Hilbert space of the signature kernels are Cameron-Martin spaces of certain Gaussian processes. This paves the way towards uncertainty quantification for signature kernel regression.
How (Implicit) Regularization of ReLU Neural Networks Characterizes the Learned Function -- Part II: the Multi-D Case of Two Layers with Random First Layer
Mar 20, 2023


Abstract:Randomized neural networks (randomized NNs), where only the terminal layer's weights are optimized constitute a powerful model class to reduce computational time in training the neural network model. At the same time, these models generalize surprisingly well in various regression and classification tasks. In this paper, we give an exact macroscopic characterization (i.e., a characterization in function space) of the generalization behavior of randomized, shallow NNs with ReLU activation (RSNs). We show that RSNs correspond to a generalized additive model (GAM)-typed regression in which infinitely many directions are considered: the infinite generalized additive model (IGAM). The IGAM is formalized as solution to an optimization problem in function space for a specific regularization functional and a fairly general loss. This work is an extension to multivariate NNs of prior work, where we showed how wide RSNs with ReLU activation behave like spline regression under certain conditions and if the input is one-dimensional.
Optimal Estimation of Generic Dynamics by Path-Dependent Neural Jump ODEs
Jun 28, 2022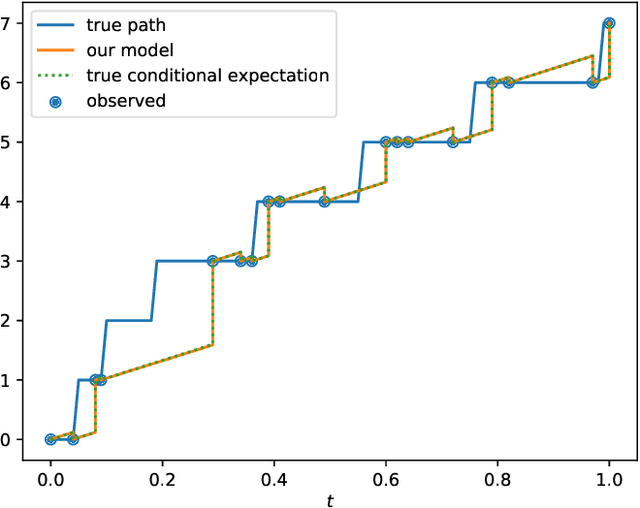

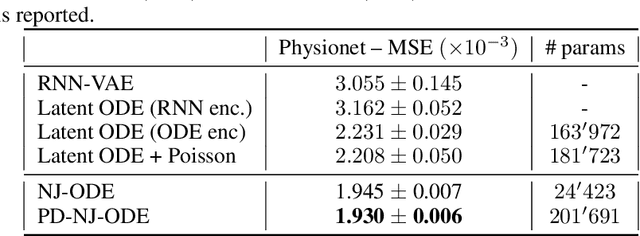
Abstract:This paper studies the problem of forecasting general stochastic processes using an extension of the Neural Jump ODE (NJ-ODE) framework. While NJ-ODE was the first framework to establish convergence guarantees for the prediction of irregularly observed time-series, these results were limited to data stemming from It\^o-diffusions with complete observations, in particular Markov processes where all coordinates are observed simultaneously. In this work, we generalise these results to generic, possibly non-Markovian or discontinuous, stochastic processes with incomplete observations, by utilising the reconstruction properties of the signature transform. These theoretical results are supported by empirical studies, where it is shown that the path-dependent NJ-ODE outperforms the original NJ-ODE framework in the case of non-Markovian data.
Applications of Signature Methods to Market Anomaly Detection
Feb 08, 2022
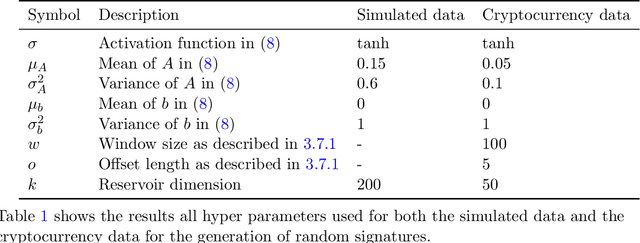
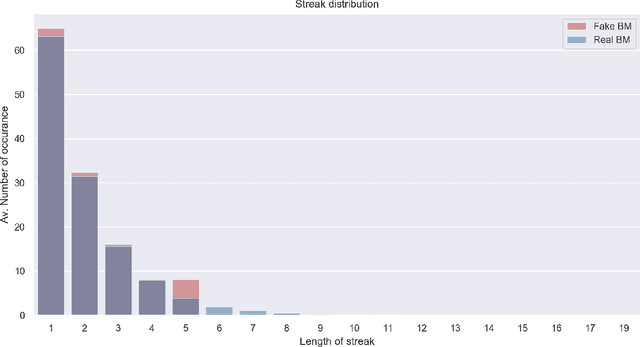
Abstract:Anomaly detection is the process of identifying abnormal instances or events in data sets which deviate from the norm significantly. In this study, we propose a signatures based machine learning algorithm to detect rare or unexpected items in a given data set of time series type. We present applications of signature or randomized signature as feature extractors for anomaly detection algorithms; additionally we provide an easy, representation theoretic justification for the construction of randomized signatures. Our first application is based on synthetic data and aims at distinguishing between real and fake trajectories of stock prices, which are indistinguishable by visual inspection. We also show a real life application by using transaction data from the cryptocurrency market. In this case, we are able to identify pump and dump attempts organized on social networks with F1 scores up to 88% by means of our unsupervised learning algorithm, thus achieving results that are close to the state-of-the-art in the field based on supervised learning.
Infinite width (finite depth) neural networks benefit from multi-task learning unlike shallow Gaussian Processes -- an exact quantitative macroscopic characterization
Jan 05, 2022
Abstract:We prove in this paper that optimizing wide ReLU neural networks (NNs) with at least one hidden layer using l2-regularization on the parameters enforces multi-task learning due to representation-learning - also in the limit of width to infinity. This is in contrast to multiple other results in the literature, in which idealized settings are assumed and where wide (ReLU)-NNs loose their ability to benefit from multi-task learning in the infinite width limit. We deduce the ability of multi-task learning from proving an exact quantitative macroscopic characterization of the learned NN in an appropriate function space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge