Solving stochastic partial differential equations using neural networks in the Wiener chaos expansion

In this paper, we solve stochastic partial differential equations (SPDEs) numerically by using (possibly random) neural networks in the truncated Wiener chaos expansion of their corresponding solution. Moreover, we provide some approximation rates for learning the solution of SPDEs with additive and/or multiplicative noise. Finally, we apply our results in numerical examples to approximate the solution of three SPDEs: the stochastic heat equation, the Heath-Jarrow-Morton equation, and the Zakai equation.

Universal approximation results for neural networks with non-polynomial activation function over non-compact domains

In this paper, we generalize the universal approximation property of single-hidden-layer feed-forward neural networks beyond the classical formulation over compact domains. More precisely, by assuming that the activation function is non-polynomial, we derive universal approximation results for neural networks within function spaces over non-compact subsets of a Euclidean space, e.g., weighted spaces, $L^p$-spaces, and (weighted) Sobolev spaces over unbounded domains, where the latter includes the approximation of the (weak) derivatives. Furthermore, we provide some dimension-independent rates for approximating a function with sufficiently regular and integrable Fourier transform by neural networks with non-polynomial activation function.

Full error analysis of the random deep splitting method for nonlinear parabolic PDEs and PIDEs with infinite activity

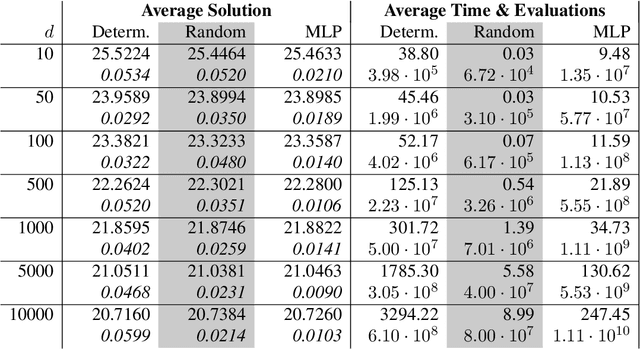
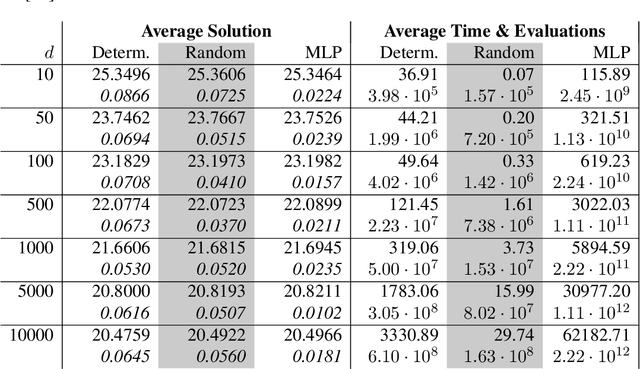
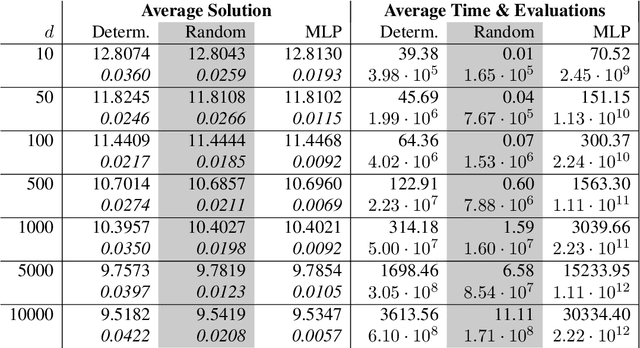
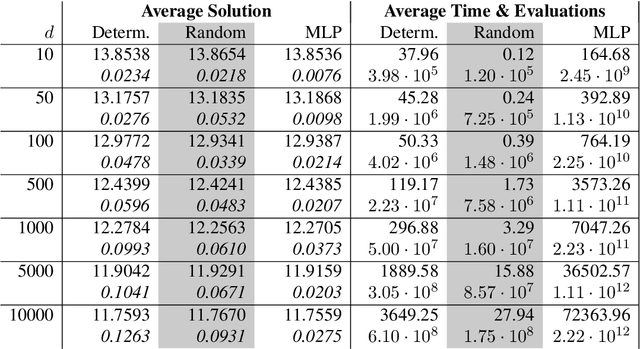
In this paper, we present a randomized extension of the deep splitting algorithm introduced in [Beck, Becker, Cheridito, Jentzen, and Neufeld (2021)] using random neural networks suitable to approximately solve both high-dimensional nonlinear parabolic PDEs and PIDEs with jumps having (possibly) infinite activity. We provide a full error analysis of our so-called random deep splitting method. In particular, we prove that our random deep splitting method converges to the (unique viscosity) solution of the nonlinear PDE or PIDE under consideration. Moreover, we empirically analyze our random deep splitting method by considering several numerical examples including both nonlinear PDEs and nonlinear PIDEs relevant in the context of pricing of financial derivatives under default risk. In particular, we empirically demonstrate in all examples that our random deep splitting method can approximately solve nonlinear PDEs and PIDEs in 10'000 dimensions within seconds.

Universal Approximation Property of Random Neural Networks

In this paper, we study random neural networks which are single-hidden-layer feedforward neural networks whose weights and biases are randomly initialized. After this random initialization, only the linear readout needs to be trained, which can be performed efficiently, e.g., by the least squares method. By viewing random neural networks as Banach space-valued random variables, we prove a universal approximation theorem within a large class of Bochner spaces. Hereby, the corresponding Banach space can be significantly more general than the space of continuous functions over a compact subset of a Euclidean space, namely, e.g., an $L^p$-space or a Sobolev space, where the latter includes the approximation of the derivatives. Moreover, we derive approximation rates and an explicit algorithm to learn a deterministic function by a random neural network. In addition, we provide a full error analysis and study when random neural networks overcome the curse of dimensionality in the sense that the training costs scale at most polynomially in the input and output dimension. Furthermore, we show in two numerical examples the empirical advantages of random neural networks compared to fully trained deterministic neural networks.

Global universal approximation of functional input maps on weighted spaces

We introduce so-called functional input neural networks defined on a possibly infinite dimensional weighted space with values also in a possibly infinite dimensional output space. To this end, we use an additive family as hidden layer maps and a non-linear activation function applied to each hidden layer. Relying on Stone-Weierstrass theorems on weighted spaces, we can prove a global universal approximation result for generalizations of continuous functions going beyond the usual approximation on compact sets. This then applies in particular to approximation of (non-anticipative) path space functionals via functional input neural networks. As a further application of the weighted Stone-Weierstrass theorem we prove a global universal approximation result for linear functions of the signature. We also introduce the viewpoint of Gaussian process regression in this setting and show that the reproducing kernel Hilbert space of the signature kernels are Cameron-Martin spaces of certain Gaussian processes. This paves the way towards uncertainty quantification for signature kernel regression.

Chaotic Hedging with Iterated Integrals and Neural Networks

In this paper, we extend the Wiener-Ito chaos decomposition to the class of diffusion processes, whose drift and diffusion coefficient are of linear growth. By omitting the orthogonality in the chaos expansion, we are able to show that every $p$-integrable functional, for $p \in [1,\infty)$, can be represented as sum of iterated integrals of the underlying process. Using a truncated sum of this expansion and (possibly random) neural networks for the integrands, whose parameters are learned in a machine learning setting, we show that every financial derivative can be approximated arbitrarily well in the $L^p$-sense. Moreover, the hedging strategy of the approximating financial derivative can be computed in closed form.