Certifiable Boolean Reasoning Is Universal

The proliferation of agentic systems has thrust the reasoning capabilities of AI into the forefront of contemporary machine learning. While it is known that there \emph{exist} neural networks which can reason through any Boolean task $f:\{0,1\}^B\to\{0,1\}$, in the sense that they emulate Boolean circuits with fan-in $2$ and fan-out $1$ gates, trained models have been repeatedly demonstrated to fall short of these theoretical ideals. This raises the question: \textit{Can one exhibit a deep learning model which \textbf{certifiably} always reasons and can \textbf{universally} reason through any Boolean task?} Moreover, such a model should ideally require few parameters to solve simple Boolean tasks. We answer this question affirmatively by exhibiting a deep learning architecture which parameterizes distributions over Boolean circuits with the guarantee that, for every parameter configuration, a sample is almost surely a valid Boolean circuit (and hence admits an intrinsic circuit-level certificate). We then prove a universality theorem: for any Boolean $f:\{0,1\}^B\to\{0,1\}$, there exists a parameter configuration under which the sampled circuit computes $f$ with arbitrarily high probability. When $f$ is an $\mathcal{O}(\log B)$-junta, the required number of parameters scales linearly with the input dimension $B$. Empirically, on a controlled truth-table completion benchmark aligned with our setting, the proposed architecture trains reliably and achieves high exact-match accuracy while preserving the predicted structure: every internal unit is Boolean-valued on $\{0,1\}^B$. Matched MLP baselines reach comparable accuracy, but only about $10\%$ of hidden units admit a Boolean representation; i.e.\ are two-valued over the Boolean cube.

Statistical Guarantees for Reasoning Probes on Looped Boolean Circuits

We study the statistical behaviour of reasoning probes in a stylized model of looped reasoning, given by Boolean circuits whose computational graph is a perfect $ν$-ary tree ($ν\ge 2$) and whose output is appended to the input and fed back iteratively for subsequent computation rounds. A reasoning probe has access to a sampled subset of internal computation nodes, possibly without covering the entire graph, and seeks to infer which $ν$-ary Boolean gate is executed at each queried node, representing uncertainty via a probability distribution over a fixed collection of $\mathtt{m}$ admissible $ν$-ary gates. This partial observability induces a generalization problem, which we analyze in a realizable, transductive setting. We show that, when the reasoning probe is parameterized by a graph convolutional network (GCN)-based hypothesis class and queries $N$ nodes, the worst-case generalization error attains the optimal rate $\mathcal{O}(\sqrt{\log(2/δ)}/\sqrt{N})$ with probability at least $1-δ$, for $δ\in (0,1)$. Our analysis combines snowflake metric embedding techniques with tools from statistical optimal transport. A key insight is that this optimal rate is achievable independently of graph size, owing to the existence of a low-distortion one-dimensional snowflake embedding of the induced graph metric. As a consequence, our results provide a sharp characterization of how structural properties of the computational graph govern the statistical efficiency of reasoning under partial access.

Incremental Generation is Necessity and Sufficient for Universality in Flow-Based Modelling

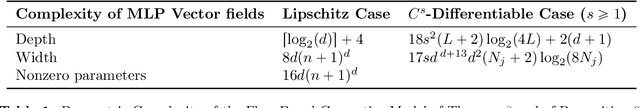
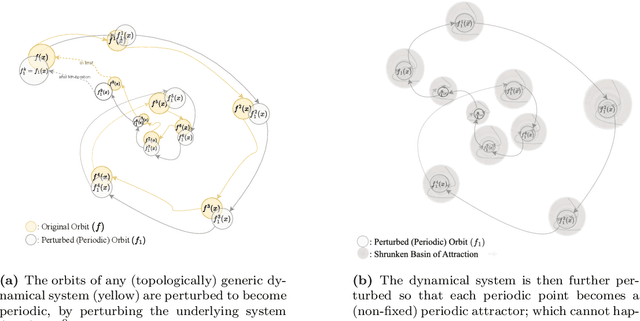
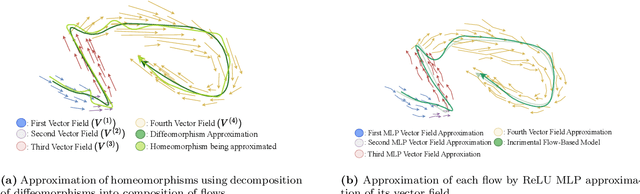
Incremental flow-based denoising models have reshaped generative modelling, but their empirical advantage still lacks a rigorous approximation-theoretic foundation. We show that incremental generation is necessary and sufficient for universal flow-based generation on the largest natural class of self-maps of $[0,1]^d$ compatible with denoising pipelines, namely the orientation-preserving homeomorphisms of $[0,1]^d$. All our guarantees are uniform on the underlying maps and hence imply approximation both samplewise and in distribution. Using a new topological-dynamical argument, we first prove an impossibility theorem: the class of all single-step autonomous flows, independently of the architecture, width, depth, or Lipschitz activation of the underlying neural network, is meagre and therefore not universal in the space of orientation-preserving homeomorphisms of $[0,1]^d$. By exploiting algebraic properties of autonomous flows, we conversely show that every orientation-preserving Lipschitz homeomorphism on $[0,1]^d$ can be approximated at rate $\mathcal{O}(n^{-1/d})$ by a composition of at most $K_d$ such flows, where $K_d$ depends only on the dimension. Under additional smoothness assumptions, the approximation rate can be made dimension-free, and $K_d$ can be chosen uniformly over the class being approximated. Finally, by linearly lifting the domain into one higher dimension, we obtain structured universal approximation results for continuous functions and for probability measures on $[0,1]^d$, the latter realized as pushforwards of empirical measures with vanishing $1$-Wasserstein error.

Learning from one graph: transductive learning guarantees via the geometry of small random worlds

Since their introduction by Kipf and Welling in $2017$, a primary use of graph convolutional networks is transductive node classification, where missing labels are inferred within a single observed graph and its feature matrix. Despite the widespread use of the network model, the statistical foundations of transductive learning remain limited, as standard inference frameworks typically rely on multiple independent samples rather than a single graph. In this work, we address these gaps by developing new concentration-of-measure tools that leverage the geometric regularities of large graphs via low-dimensional metric embeddings. The emergent regularities are captured using a random graph model; however, the methods remain applicable to deterministic graphs once observed. We establish two principal learning results. The first concerns arbitrary deterministic $k$-vertex graphs, and the second addresses random graphs that share key geometric properties with an Erd\H{o}s-R\'{e}nyi graph $\mathbf{G}=\mathbf{G}(k,p)$ in the regime $p \in \mathcal{O}((\log (k)/k)^{1/2})$. The first result serves as the basis for and illuminates the second. We then extend these results to the graph convolutional network setting, where additional challenges arise. Lastly, our learning guarantees remain informative even with a few labelled nodes $N$ and achieve the optimal nonparametric rate $\mathcal{O}(N^{-1/2})$ as $N$ grows.

Generative Neural Operators of Log-Complexity Can Simultaneously Solve Infinitely Many Convex Programs

Neural operators (NOs) are a class of deep learning models designed to simultaneously solve infinitely many related problems by casting them into an infinite-dimensional space, whereon these NOs operate. A significant gap remains between theory and practice: worst-case parameter bounds from universal approximation theorems suggest that NOs may require an unrealistically large number of parameters to solve most operator learning problems, which stands in direct opposition to a slew of experimental evidence. This paper closes that gap for a specific class of {NOs}, generative {equilibrium operators} (GEOs), using (realistic) finite-dimensional deep equilibrium layers, when solving families of convex optimization problems over a separable Hilbert space $X$. Here, the inputs are smooth, convex loss functions on $X$, and outputs are the associated (approximate) solutions to the optimization problem defined by each input loss. We show that when the input losses lie in suitable infinite-dimensional compact sets, our GEO can uniformly approximate the corresponding solutions to arbitrary precision, with rank, depth, and width growing only logarithmically in the reciprocal of the approximation error. We then validate both our theoretical results and the trainability of GEOs on three applications: (1) nonlinear PDEs, (2) stochastic optimal control problems, and (3) hedging problems in mathematical finance under liquidity constraints.

LoRA Fine-Tuning Without GPUs: A CPU-Efficient Meta-Generation Framework for LLMs

Low-Rank Adapters (LoRAs) have transformed the fine-tuning of Large Language Models (LLMs) by enabling parameter-efficient updates. However, their widespread adoption remains limited by the reliance on GPU-based training. In this work, we propose a theoretically grounded approach to LoRA fine-tuning designed specifically for users with limited computational resources, particularly those restricted to standard laptop CPUs. Our method learns a meta-operator that maps any input dataset, represented as a probability distribution, to a set of LoRA weights by leveraging a large bank of pre-trained adapters for the Mistral-7B-Instruct-v0.2 model. Instead of performing new gradient-based updates, our pipeline constructs adapters via lightweight combinations of existing LoRAs directly on CPU. While the resulting adapters do not match the performance of GPU-trained counterparts, they consistently outperform the base Mistral model on downstream tasks, offering a practical and accessible alternative to traditional GPU-based fine-tuning.

Sharp Generalization Bounds for Foundation Models with Asymmetric Randomized Low-Rank Adapters

Low-Rank Adaptation (LoRA) has emerged as a widely adopted parameter-efficient fine-tuning (PEFT) technique for foundation models. Recent work has highlighted an inherent asymmetry in the initialization of LoRA's low-rank factors, which has been present since its inception and was presumably derived experimentally. This paper focuses on providing a comprehensive theoretical characterization of asymmetric LoRA with frozen random factors. First, while existing research provides upper-bound generalization guarantees based on averages over multiple experiments, the behaviour of a single fine-tuning run with specific random factors remains an open question. We address this by investigating the concentration of the typical LoRA generalization gap around its mean. Our main upper bound reveals a sample complexity of $\tilde{\mathcal{O}}\left(\frac{\sqrt{r}}{\sqrt{N}}\right)$ with high probability for rank $r$ LoRAs trained on $N$ samples. Additionally, we also determine the fundamental limits in terms of sample efficiency, establishing a matching lower bound of $\mathcal{O}\left(\frac{1}{\sqrt{N}}\right)$. By more closely reflecting the practical scenario of a single fine-tuning run, our findings offer crucial insights into the reliability and practicality of asymmetric LoRA.

Online Federation For Mixtures of Proprietary Agents with Black-Box Encoders

Most industry-standard generative AIs and feature encoders are proprietary, offering only black-box access: their outputs are observable, but their internal parameters and architectures remain hidden from the end-user. This black-box access is especially limiting when constructing mixture-of-expert type ensemble models since the user cannot optimize each proprietary AI's internal parameters. Our problem naturally lends itself to a non-competitive game-theoretic lens where each proprietary AI (agent) is inherently competing against the other AI agents, with this competition arising naturally due to their obliviousness of the AI's to their internal structure. In contrast, the user acts as a central planner trying to synchronize the ensemble of competing AIs. We show the existence of the unique Nash equilibrium in the online setting, which we even compute in closed-form by eliciting a feedback mechanism between any given time series and the sequence generated by each (proprietary) AI agent. Our solution is implemented as a decentralized, federated-learning algorithm in which each agent optimizes their structure locally on their machine without ever releasing any internal structure to the others. We obtain refined expressions for pre-trained models such as transformers, random feature models, and echo-state networks. Our ``proprietary federated learning'' algorithm is implemented on a range of real-world and synthetic time-series benchmarks. It achieves orders-of-magnitude improvements in predictive accuracy over natural benchmarks, of which there are surprisingly few due to this natural problem still being largely unexplored.

Kolmogorov-Arnold Networks: Approximation and Learning Guarantees for Functions and their Derivatives

Inspired by the Kolmogorov-Arnold superposition theorem, Kolmogorov-Arnold Networks (KANs) have recently emerged as an improved backbone for most deep learning frameworks, promising more adaptivity than their multilayer perception (MLP) predecessor by allowing for trainable spline-based activation functions. In this paper, we probe the theoretical foundations of the KAN architecture by showing that it can optimally approximate any Besov function in $B^{s}_{p,q}(\mathcal{X})$ on a bounded open, or even fractal, domain $\mathcal{X}$ in $\mathbb{R}^d$ at the optimal approximation rate with respect to any weaker Besov norm $B^{\alpha}_{p,q}(\mathcal{X})$; where $\alpha < s$. We complement our approximation guarantee with a dimension-free estimate on the sample complexity of a residual KAN model when learning a function of Besov regularity from $N$ i.i.d. noiseless samples. Our KAN architecture incorporates contemporary deep learning wisdom by leveraging residual/skip connections between layers.

Generative Market Equilibrium Models with Stable Adversarial Learning via Reinforcement

We present a general computational framework for solving continuous-time financial market equilibria under minimal modeling assumptions while incorporating realistic financial frictions, such as trading costs, and supporting multiple interacting agents. Inspired by generative adversarial networks (GANs), our approach employs a novel generative deep reinforcement learning framework with a decoupling feedback system embedded in the adversarial training loop, which we term as the \emph{reinforcement link}. This architecture stabilizes the training dynamics by incorporating feedback from the discriminator. Our theoretically guided feedback mechanism enables the decoupling of the equilibrium system, overcoming challenges that hinder conventional numerical algorithms. Experimentally, our algorithm not only learns but also provides testable predictions on how asset returns and volatilities emerge from the endogenous trading behavior of market participants, where traditional analytical methods fall short. The design of our model is further supported by an approximation guarantee.