Learning from one graph: transductive learning guarantees via the geometry of small random worlds

Since their introduction by Kipf and Welling in $2017$, a primary use of graph convolutional networks is transductive node classification, where missing labels are inferred within a single observed graph and its feature matrix. Despite the widespread use of the network model, the statistical foundations of transductive learning remain limited, as standard inference frameworks typically rely on multiple independent samples rather than a single graph. In this work, we address these gaps by developing new concentration-of-measure tools that leverage the geometric regularities of large graphs via low-dimensional metric embeddings. The emergent regularities are captured using a random graph model; however, the methods remain applicable to deterministic graphs once observed. We establish two principal learning results. The first concerns arbitrary deterministic $k$-vertex graphs, and the second addresses random graphs that share key geometric properties with an Erd\H{o}s-R\'{e}nyi graph $\mathbf{G}=\mathbf{G}(k,p)$ in the regime $p \in \mathcal{O}((\log (k)/k)^{1/2})$. The first result serves as the basis for and illuminates the second. We then extend these results to the graph convolutional network setting, where additional challenges arise. Lastly, our learning guarantees remain informative even with a few labelled nodes $N$ and achieve the optimal nonparametric rate $\mathcal{O}(N^{-1/2})$ as $N$ grows.

In-Context Operator Learning for Linear Propagator Models

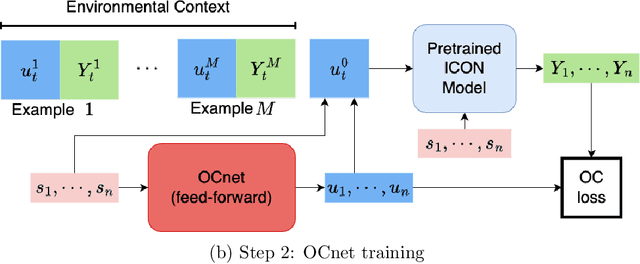
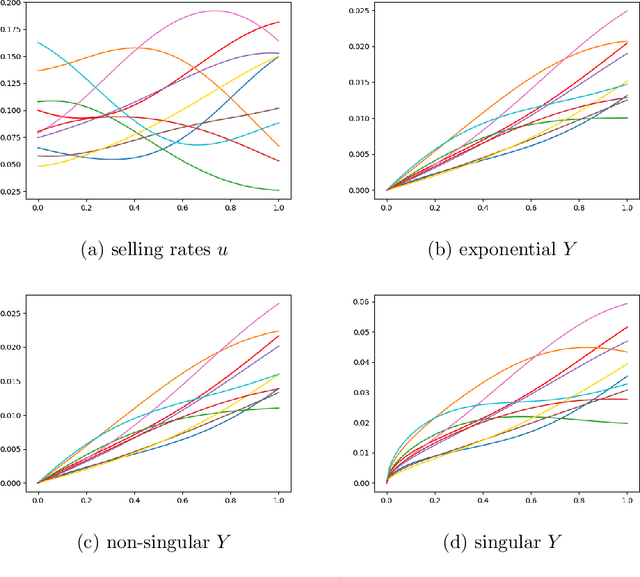
We study operator learning in the context of linear propagator models for optimal order execution problems with transient price impact \`a la Bouchaud et al. (2004) and Gatheral (2010). Transient price impact persists and decays over time according to some propagator kernel. Specifically, we propose to use In-Context Operator Networks (ICON), a novel transformer-based neural network architecture introduced by Yang et al. (2023), which facilitates data-driven learning of operators by merging offline pre-training with an online few-shot prompting inference. First, we train ICON to learn the operator from various propagator models that maps the trading rate to the induced transient price impact. The inference step is then based on in-context prediction, where ICON is presented only with a few examples. We illustrate that ICON is capable of accurately inferring the underlying price impact model from the data prompts, even with propagator kernels not seen in the training data. In a second step, we employ the pre-trained ICON model provided with context as a surrogate operator in solving an optimal order execution problem via a neural network control policy, and demonstrate that the exact optimal execution strategies from Abi Jaber and Neuman (2022) for the models generating the context are correctly retrieved. Our introduced methodology is very general, offering a new approach to solving optimal stochastic control problems with unknown state dynamics, inferred data-efficiently from a limited number of examples by leveraging the few-shot and transfer learning capabilities of transformer networks.

Pricing options on flow forwards by neural networks in Hilbert space

We propose a new methodology for pricing options on flow forwards by applying infinite-dimensional neural networks. We recast the pricing problem as an optimization problem in a Hilbert space of real-valued function on the positive real line, which is the state space for the term structure dynamics. This optimization problem is solved by facilitating a novel feedforward neural network architecture designed for approximating continuous functions on the state space. The proposed neural net is built upon the basis of the Hilbert space. We provide an extensive case study that shows excellent numerical efficiency, with superior performance over that of a classical neural net trained on sampling the term structure curves.