In-Context Operator Learning for Linear Propagator Models

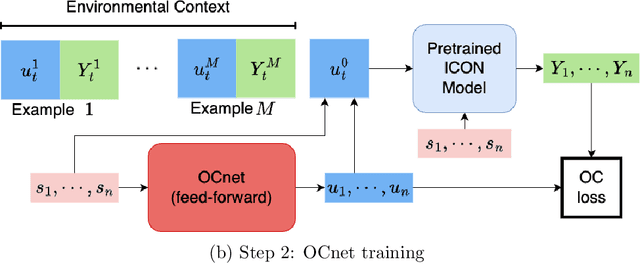
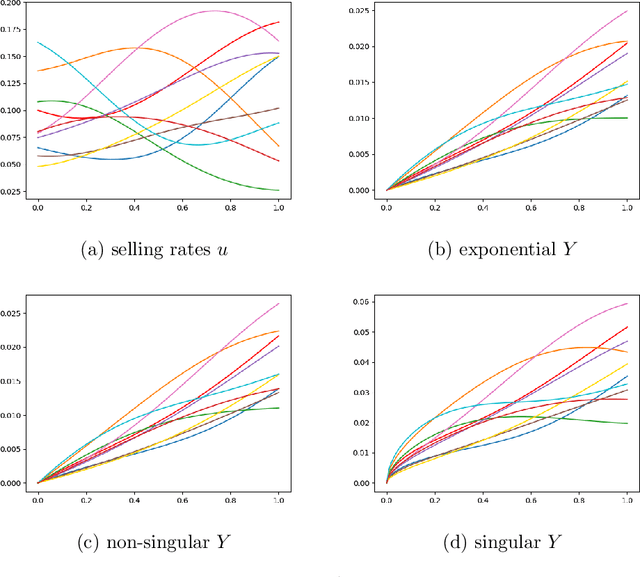
We study operator learning in the context of linear propagator models for optimal order execution problems with transient price impact \`a la Bouchaud et al. (2004) and Gatheral (2010). Transient price impact persists and decays over time according to some propagator kernel. Specifically, we propose to use In-Context Operator Networks (ICON), a novel transformer-based neural network architecture introduced by Yang et al. (2023), which facilitates data-driven learning of operators by merging offline pre-training with an online few-shot prompting inference. First, we train ICON to learn the operator from various propagator models that maps the trading rate to the induced transient price impact. The inference step is then based on in-context prediction, where ICON is presented only with a few examples. We illustrate that ICON is capable of accurately inferring the underlying price impact model from the data prompts, even with propagator kernels not seen in the training data. In a second step, we employ the pre-trained ICON model provided with context as a surrogate operator in solving an optimal order execution problem via a neural network control policy, and demonstrate that the exact optimal execution strategies from Abi Jaber and Neuman (2022) for the models generating the context are correctly retrieved. Our introduced methodology is very general, offering a new approach to solving optimal stochastic control problems with unknown state dynamics, inferred data-efficiently from a limited number of examples by leveraging the few-shot and transfer learning capabilities of transformer networks.

On Parametric Optimal Execution and Machine Learning Surrogates

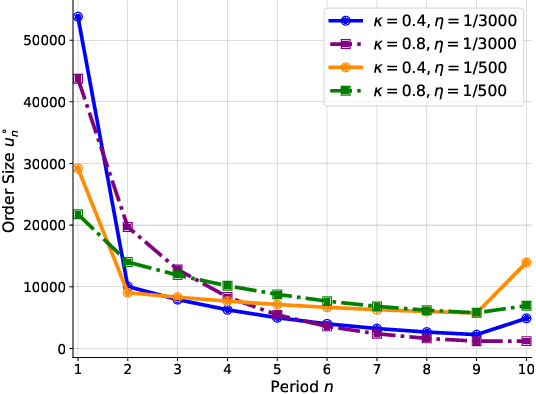
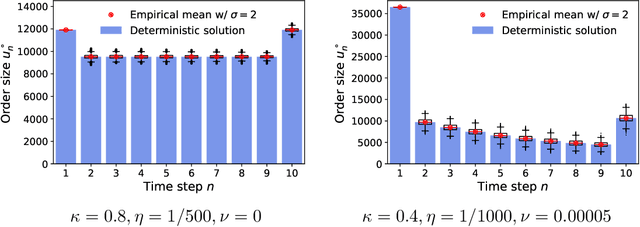
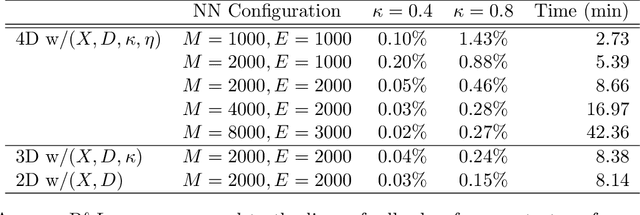
We investigate optimal order execution problems in discrete time with instantaneous price impact and stochastic resilience. First, in the setting of linear transient price impact we derive a closed-form recursion for the optimal strategy, extending the deterministic results from Obizhaeva and Wang (J Financial Markets, 2013). Second, we develop a numerical algorithm based on dynamic programming and deep learning for the case of nonlinear transient price impact as proposed by Bouchaud et al. (Quant. Finance, 2004). Specifically, we utilize an actor-critic framework that constructs two neural-network (NN) surrogates for the value function and the feedback control. The flexible scalability of NN functional approximators enables parametric learning, i.e., incorporating several model or market parameters as part of the input space. Precise calibration of price impact, resilience, etc., is known to be extremely challenging and hence it is critical to understand sensitivity of the execution policy to these parameters. Our NN learner organically scales across multiple input dimensions and is shown to accurately approximate optimal strategies across a wide range of parameter configurations. We provide a fully reproducible Jupyter Notebook with our NN implementation, which is of independent pedagogical interest, demonstrating the ease of use of NN surrogates in (parametric) stochastic control problems.