Expressive Mortality Models through Gaussian Process Kernels

We develop a flexible Gaussian Process (GP) framework for learning the covariance structure of Age- and Year-specific mortality surfaces. Utilizing the additive and multiplicative structure of GP kernels, we design a genetic programming algorithm to search for the most expressive kernel for a given population. Our compositional search builds off the Age-Period-Cohort (APC) paradigm to construct a covariance prior best matching the spatio-temporal dynamics of a mortality dataset. We apply the resulting genetic algorithm (GA) on synthetic case studies to validate the ability of the GA to recover APC structure, and on real-life national-level datasets from the Human Mortality Database. Our machine-learning based analysis provides novel insight into the presence/absence of Cohort effects in different populations, and into the relative smoothness of mortality surfaces along the Age and Year dimensions. Our modelling work is done with the PyTorch libraries in Python and provides an in-depth investigation of employing GA to aid in compositional kernel search for GP surrogates.

On Parametric Optimal Execution and Machine Learning Surrogates

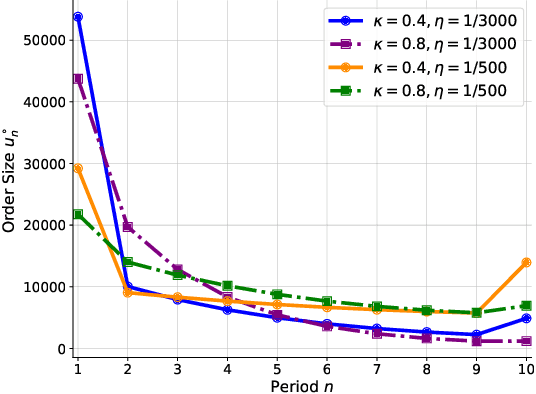
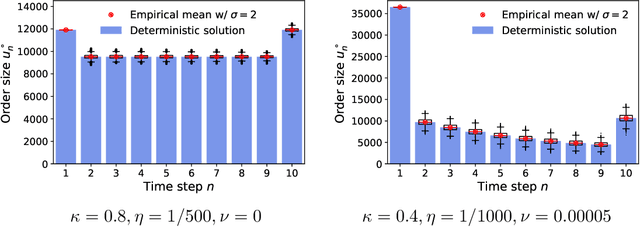
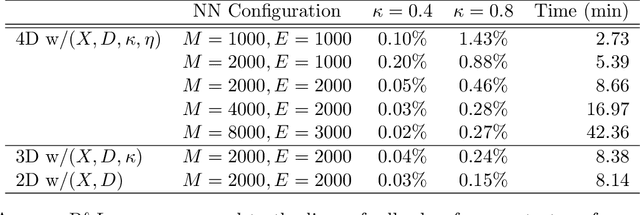
We investigate optimal order execution problems in discrete time with instantaneous price impact and stochastic resilience. First, in the setting of linear transient price impact we derive a closed-form recursion for the optimal strategy, extending the deterministic results from Obizhaeva and Wang (J Financial Markets, 2013). Second, we develop a numerical algorithm based on dynamic programming and deep learning for the case of nonlinear transient price impact as proposed by Bouchaud et al. (Quant. Finance, 2004). Specifically, we utilize an actor-critic framework that constructs two neural-network (NN) surrogates for the value function and the feedback control. The flexible scalability of NN functional approximators enables parametric learning, i.e., incorporating several model or market parameters as part of the input space. Precise calibration of price impact, resilience, etc., is known to be extremely challenging and hence it is critical to understand sensitivity of the execution policy to these parameters. Our NN learner organically scales across multiple input dimensions and is shown to accurately approximate optimal strategies across a wide range of parameter configurations. We provide a fully reproducible Jupyter Notebook with our NN implementation, which is of independent pedagogical interest, demonstrating the ease of use of NN surrogates in (parametric) stochastic control problems.

mlOSP: Towards a Unified Implementation of Regression Monte Carlo Algorithms

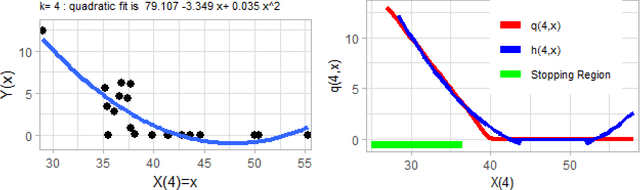
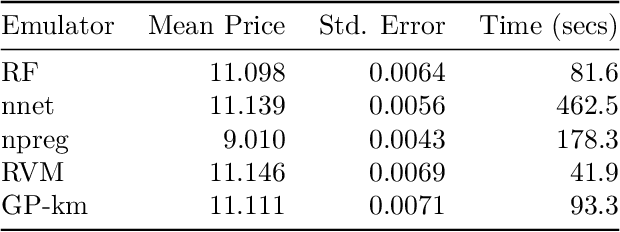
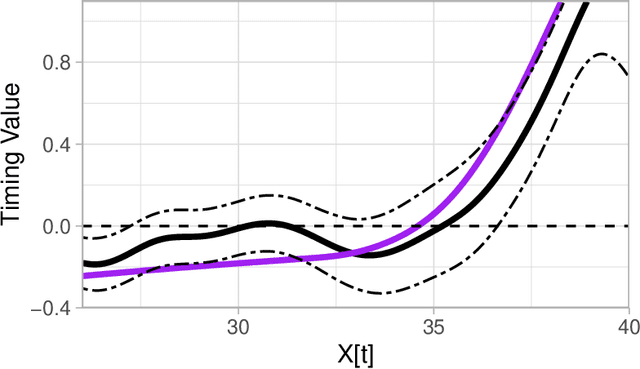
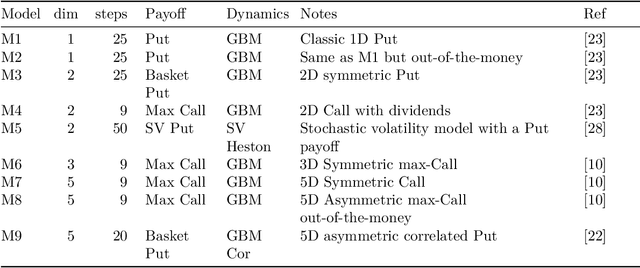
We introduce mlOSP, a computational template for Machine Learning for Optimal Stopping Problems. The template is implemented in the R statistical environment and publicly available via a GitHub repository. mlOSP presents a unified numerical implementation of Regression Monte Carlo (RMC) approaches to optimal stopping, providing a state-of-the-art, open-source, reproducible and transparent platform. Highlighting its modular nature, we present multiple novel variants of RMC algorithms, especially in terms of constructing simulation designs for training the regressors, as well as in terms of machine learning regression modules. At the same time, mlOSP nests most of the existing RMC schemes, allowing for a consistent and verifiable benchmarking of extant algorithms. The article contains extensive R code snippets and figures, and serves the dual role of presenting new RMC features and as a vignette to the underlying software package.

KrigHedge: Gaussian Process Surrogates for Delta Hedging

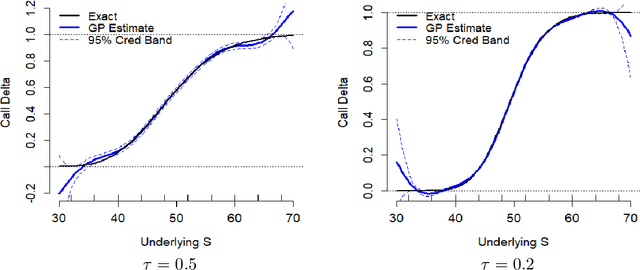
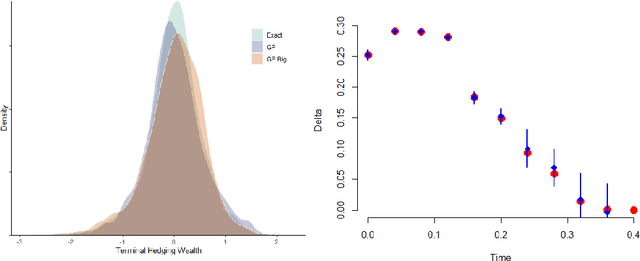
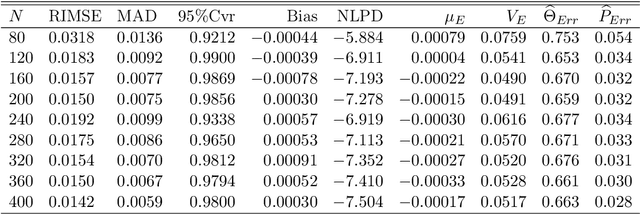
We investigate a machine learning approach to option Greeks approximation based on Gaussian process (GP) surrogates. The method takes in noisily observed option prices, fits a nonparametric input-output map and then analytically differentiates the latter to obtain the various price sensitivities. Our motivation is to compute Greeks in cases where direct computation is expensive, such as in local volatility models, or can only ever be done approximately. We provide a detailed analysis of numerous aspects of GP surrogates, including choice of kernel family, simulation design, choice of trend function and impact of noise. We further discuss the application to Delta hedging, including a new Lemma that relates quality of the Delta approximation to discrete-time hedging loss. Results are illustrated with two extensive case studies that consider estimation of Delta, Theta and Gamma and benchmark approximation quality and uncertainty quantification using a variety of statistical metrics. Among our key take-aways are the recommendation to use Matern kernels, the benefit of including virtual training points to capture boundary conditions, and the significant loss of fidelity when training on stock-path-based datasets.

Adaptive Batching for Gaussian Process Surrogates with Application in Noisy Level Set Estimation

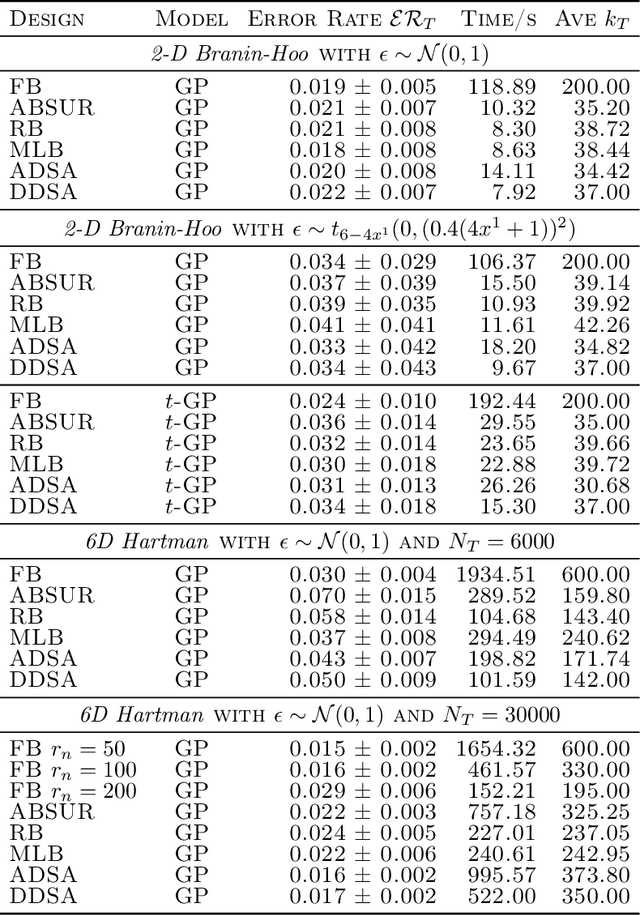
We develop adaptive replicated designs for Gaussian process metamodels of stochastic experiments. Adaptive batching is a natural extension of sequential design heuristics with the benefit of replication growing as response features are learned, inputs concentrate, and the metamodeling overhead rises. Motivated by the problem of learning the level set of the mean simulator response we develop four novel schemes: Multi-Level Batching (MLB), Ratchet Batching (RB), Adaptive Batched Stepwise Uncertainty Reduction (ABSUR), Adaptive Design with Stepwise Allocation (ADSA) and Deterministic Design with Stepwise Allocation (DDSA). Our algorithms simultaneously (MLB, RB and ABSUR) or sequentially (ADSA and DDSA) determine the sequential design inputs and the respective number of replicates. Illustrations using synthetic examples and an application in quantitative finance (Bermudan option pricing via Regression Monte Carlo) show that adaptive batching brings significant computational speed-ups with minimal loss of modeling fidelity.

Probabilistic Bisection with Spatial Metamodels

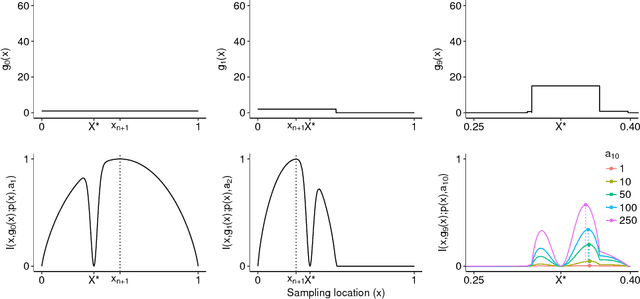
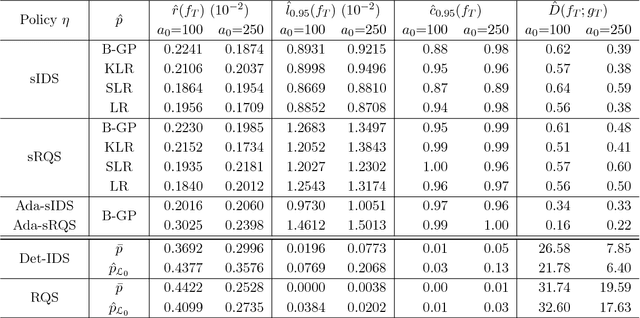
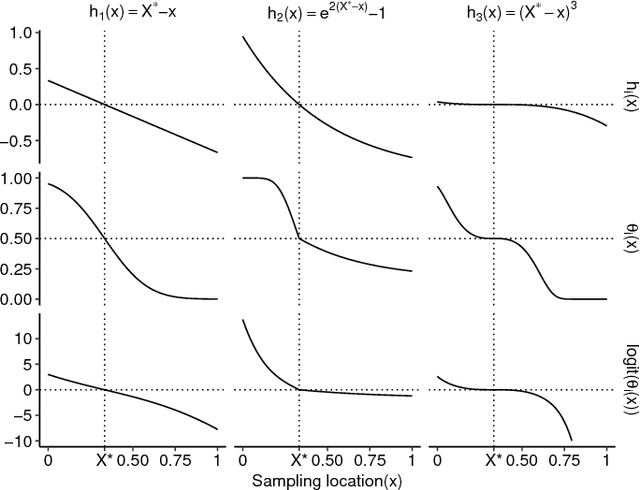
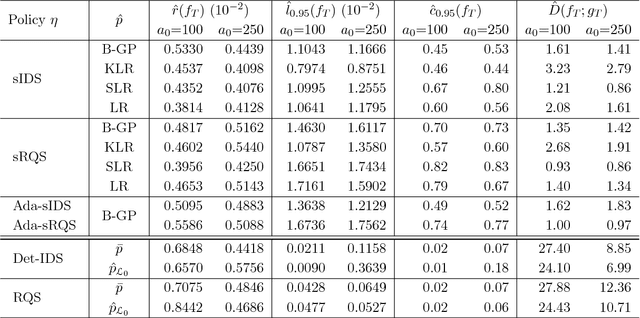
Probabilistic Bisection Algorithm performs root finding based on knowledge acquired from noisy oracle responses. We consider the generalized PBA setting (G-PBA) where the statistical distribution of the oracle is unknown and location-dependent, so that model inference and Bayesian knowledge updating must be performed simultaneously. To this end, we propose to leverage the spatial structure of a typical oracle by constructing a statistical surrogate for the underlying logistic regression step. We investigate several non-parametric surrogates, including Binomial Gaussian Processes (B-GP), Polynomial, Kernel, and Spline Logistic Regression. In parallel, we develop sampling policies that adaptively balance learning the oracle distribution and learning the root. One of our proposals mimics active learning with B-GPs and provides a novel look-ahead predictive variance formula. The resulting gains of our Spatial PBA algorithm relative to earlier G-PBA models are illustrated with synthetic examples and a challenging stochastic root finding problem from Bermudan option pricing.

Sequential Design for Ranking Response Surfaces

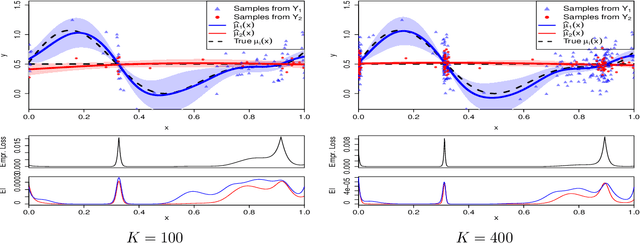
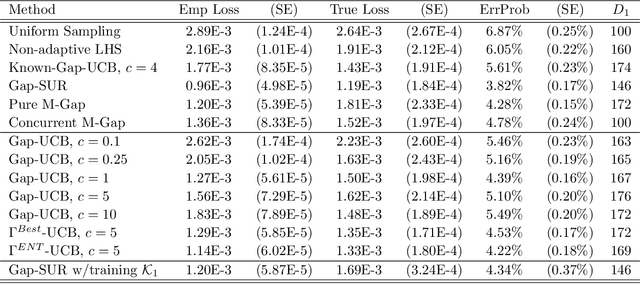
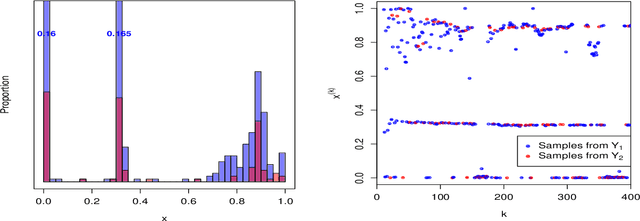
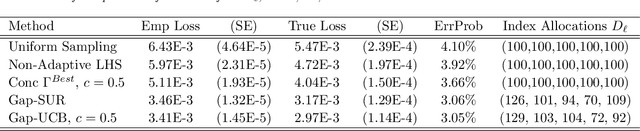
We propose and analyze sequential design methods for the problem of ranking several response surfaces. Namely, given $L \ge 2$ response surfaces over a continuous input space $\cal X$, the aim is to efficiently find the index of the minimal response across the entire $\cal X$. The response surfaces are not known and have to be noisily sampled one-at-a-time. This setting is motivated by stochastic control applications and requires joint experimental design both in space and response-index dimensions. To generate sequential design heuristics we investigate stepwise uncertainty reduction approaches, as well as sampling based on posterior classification complexity. We also make connections between our continuous-input formulation and the discrete framework of pure regret in multi-armed bandits. To model the response surfaces we utilize kriging surrogates. Several numerical examples using both synthetic data and an epidemics control problem are provided to illustrate our approach and the efficacy of respective adaptive designs.

Sequential Design for Optimal Stopping Problems

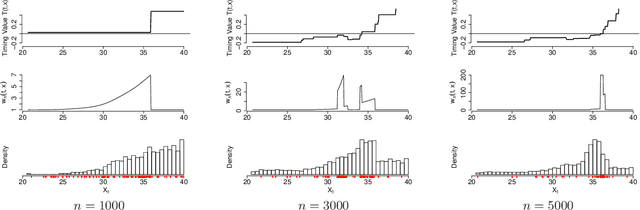
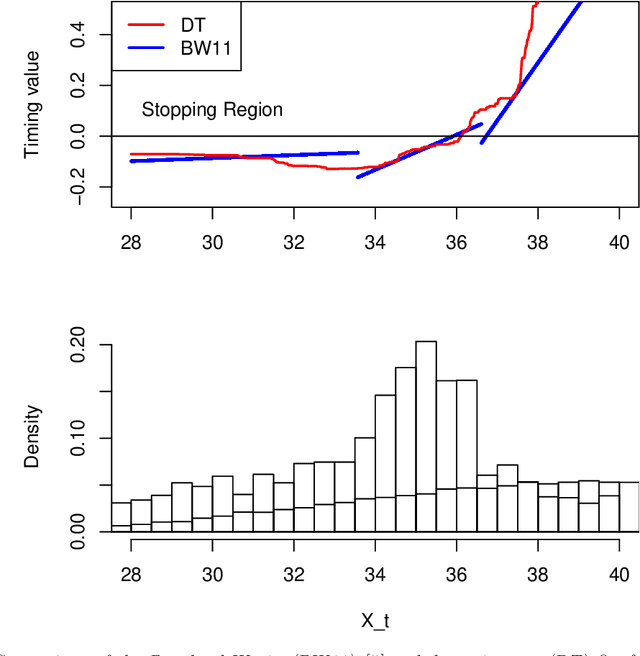
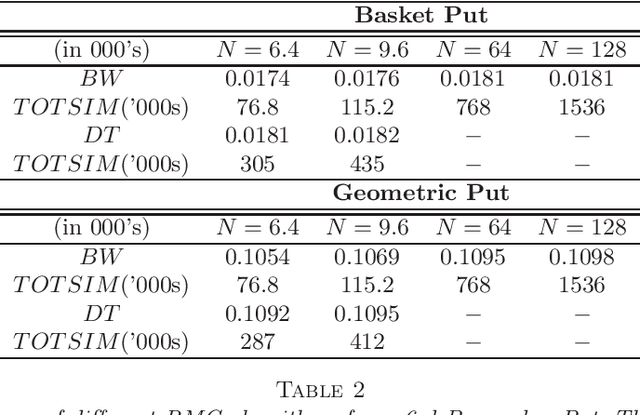
We propose a new approach to solve optimal stopping problems via simulation. Working within the backward dynamic programming/Snell envelope framework, we augment the methodology of Longstaff-Schwartz that focuses on approximating the stopping strategy. Namely, we introduce adaptive generation of the stochastic grids anchoring the simulated sample paths of the underlying state process. This allows for active learning of the classifiers partitioning the state space into the continuation and stopping regions. To this end, we examine sequential design schemes that adaptively place new design points close to the stopping boundaries. We then discuss dynamic regression algorithms that can implement such recursive estimation and local refinement of the classifiers. The new algorithm is illustrated with a variety of numerical experiments, showing that an order of magnitude savings in terms of design size can be achieved. We also compare with existing benchmarks in the context of pricing multi-dimensional Bermudan options.