Nonparametric Instrumental Variable Regression through Stochastic Approximate Gradients

This paper proposes SAGD-IV, a novel framework for conducting nonparametric instrumental variable (NPIV) regression by employing stochastic approximate gradients to minimize the projected populational risk. Instrumental Variables (IVs) are widely used in econometrics to address estimation problems in the presence of unobservable confounders, and the Machine Learning community has devoted significant effort to improving existing methods and devising new ones in the NPIV setting, which is known to be an ill-posed linear inverse problem. We provide theoretical support for our algorithm and further exemplify its competitive performance through empirical experiments. Furthermore, we address, with promising results, the case of binary outcomes, which has not received as much attention from the community as its continuous counterpart.

KrigHedge: Gaussian Process Surrogates for Delta Hedging

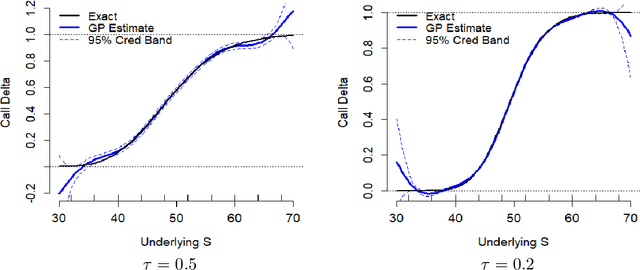
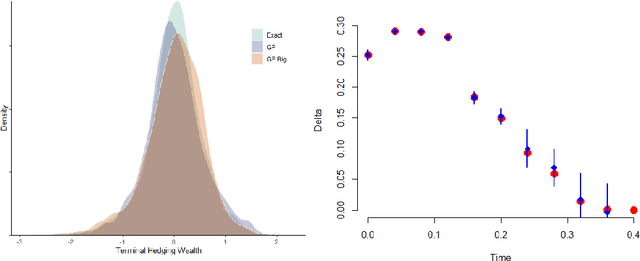
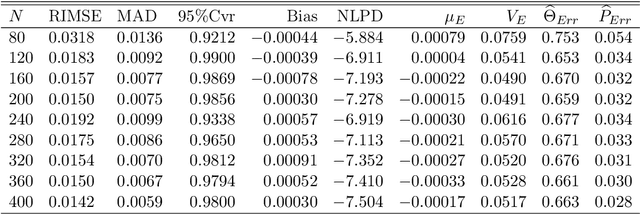
We investigate a machine learning approach to option Greeks approximation based on Gaussian process (GP) surrogates. The method takes in noisily observed option prices, fits a nonparametric input-output map and then analytically differentiates the latter to obtain the various price sensitivities. Our motivation is to compute Greeks in cases where direct computation is expensive, such as in local volatility models, or can only ever be done approximately. We provide a detailed analysis of numerous aspects of GP surrogates, including choice of kernel family, simulation design, choice of trend function and impact of noise. We further discuss the application to Delta hedging, including a new Lemma that relates quality of the Delta approximation to discrete-time hedging loss. Results are illustrated with two extensive case studies that consider estimation of Delta, Theta and Gamma and benchmark approximation quality and uncertainty quantification using a variety of statistical metrics. Among our key take-aways are the recommendation to use Matern kernels, the benefit of including virtual training points to capture boundary conditions, and the significant loss of fidelity when training on stock-path-based datasets.

Applications of the Deep Galerkin Method to Solving Partial Integro-Differential and Hamilton-Jacobi-Bellman Equations

We extend the Deep Galerkin Method (DGM) introduced in Sirignano and Spiliopoulos (2018) to solve a number of partial differential equations (PDEs) that arise in the context of optimal stochastic control and mean field games. First, we consider PDEs where the function is constrained to be positive and integrate to unity, as is the case with Fokker-Planck equations. Our approach involves reparameterizing the solution as the exponential of a neural network appropriately normalized to ensure both requirements are satisfied. This then gives rise to a partial integro-differential equation (PIDE) where the integral appearing in the equation is handled using importance sampling. Secondly, we tackle a number of Hamilton-Jacobi-Bellman (HJB) equations that appear in stochastic optimal control problems. The key contribution is that these equations are approached in their unsimplified primal form which includes an optimization problem as part of the equation. We extend the DGM algorithm to solve for the value function and the optimal control simultaneously by characterizing both as deep neural networks. Training the networks is performed by taking alternating stochastic gradient descent steps for the two functions, a technique similar in spirit to policy improvement algorithms.