C-Learner: Constrained Learning for Causal Inference and Semiparametric Statistics

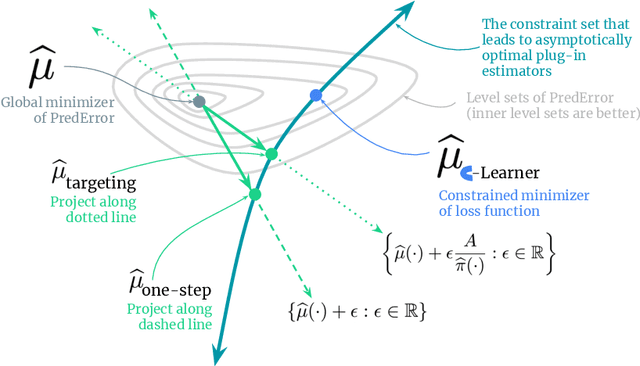
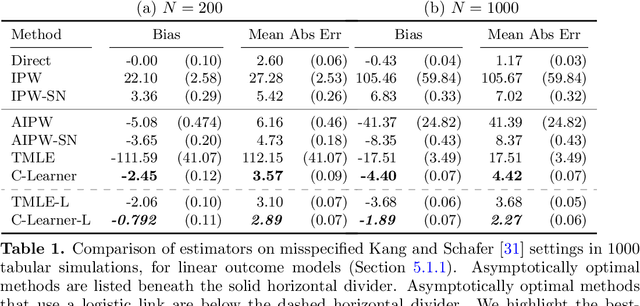
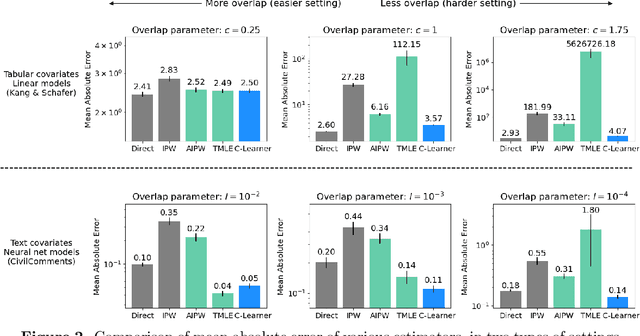
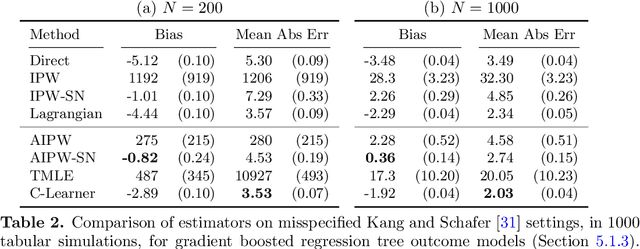
Causal estimation (e.g. of the average treatment effect) requires estimating complex nuisance parameters (e.g. outcome models). To adjust for errors in nuisance parameter estimation, we present a novel correction method that solves for the best plug-in estimator under the constraint that the first-order error of the estimator with respect to the nuisance parameter estimate is zero. Our constrained learning framework provides a unifying perspective to prominent first-order correction approaches including one-step estimation (a.k.a. augmented inverse probability weighting) and targeting (a.k.a. targeted maximum likelihood estimation). Our semiparametric inference approach, which we call the "C-Learner", can be implemented with modern machine learning methods such as neural networks and tree ensembles, and enjoys standard guarantees like semiparametric efficiency and double robustness. Empirically, we demonstrate our approach on several datasets, including those with text features that require fine-tuning language models. We observe the C-Learner matches or outperforms other asymptotically optimal estimators, with better performance in settings with less estimated overlap.

Constrained Learning for Causal Inference and Semiparametric Statistics

Causal estimation (e.g. of the average treatment effect) requires estimating complex nuisance parameters (e.g. outcome models). To adjust for errors in nuisance parameter estimation, we present a novel correction method that solves for the best plug-in estimator under the constraint that the first-order error of the estimator with respect to the nuisance parameter estimate is zero. Our constrained learning framework provides a unifying perspective to prominent first-order correction approaches including debiasing (a.k.a. augmented inverse probability weighting) and targeting (a.k.a. targeted maximum likelihood estimation). Our semiparametric inference approach, which we call the "C-Learner", can be implemented with modern machine learning methods such as neural networks and tree ensembles, and enjoys standard guarantees like semiparametric efficiency and double robustness. Empirically, we demonstrate our approach on several datasets, including those with text features that require fine-tuning language models. We observe the C-Learner matches or outperforms other asymptotically optimal estimators, with better performance in settings with less estimated overlap.

Nonparametric Instrumental Variable Regression through Stochastic Approximate Gradients

This paper proposes SAGD-IV, a novel framework for conducting nonparametric instrumental variable (NPIV) regression by employing stochastic approximate gradients to minimize the projected populational risk. Instrumental Variables (IVs) are widely used in econometrics to address estimation problems in the presence of unobservable confounders, and the Machine Learning community has devoted significant effort to improving existing methods and devising new ones in the NPIV setting, which is known to be an ill-posed linear inverse problem. We provide theoretical support for our algorithm and further exemplify its competitive performance through empirical experiments. Furthermore, we address, with promising results, the case of binary outcomes, which has not received as much attention from the community as its continuous counterpart.

Contextual Inverse Optimization: Offline and Online Learning

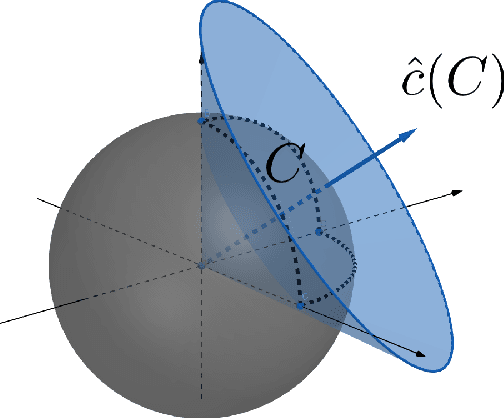
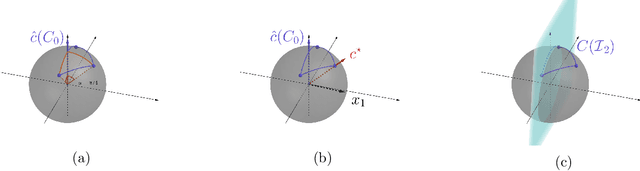
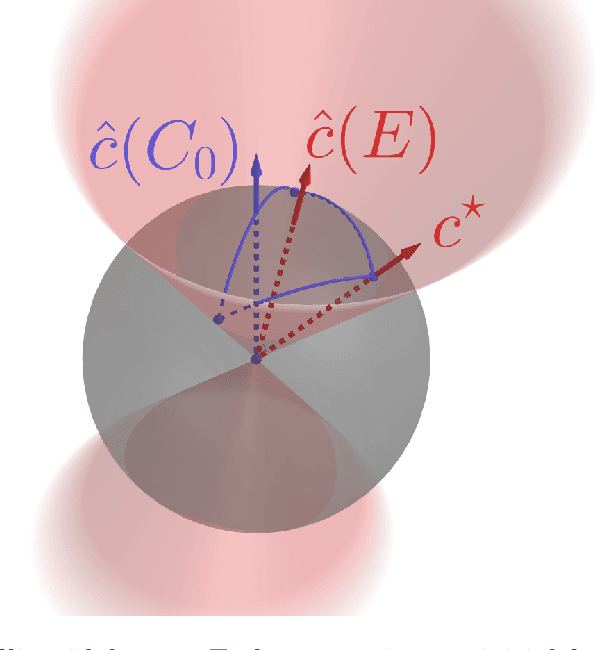
We study the problems of offline and online contextual optimization with feedback information, where instead of observing the loss, we observe, after-the-fact, the optimal action an oracle with full knowledge of the objective function would have taken. We aim to minimize regret, which is defined as the difference between our losses and the ones incurred by an all-knowing oracle. In the offline setting, the decision-maker has information available from past periods and needs to make one decision, while in the online setting, the decision-maker optimizes decisions dynamically over time based a new set of feasible actions and contextual functions in each period. For the offline setting, we characterize the optimal minimax policy, establishing the performance that can be achieved as a function of the underlying geometry of the information induced by the data. In the online setting, we leverage this geometric characterization to optimize the cumulative regret. We develop an algorithm that yields the first regret bound for this problem that is logarithmic in the time horizon.

BooST: Boosting Smooth Trees for Partial Effect Estimation in Nonlinear Regressions

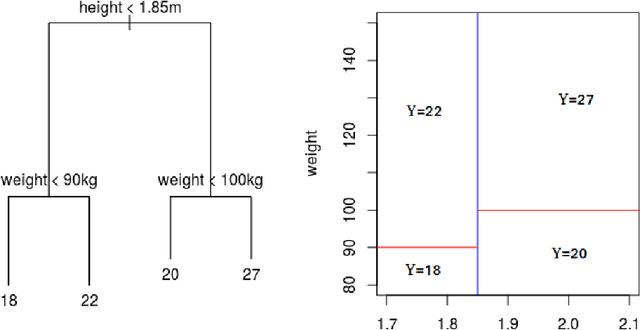
In this paper we introduce a new machine learning (ML) model for nonlinear regression called Boosting Smooth Transition Regression Trees (BooST). The main advantage of the BooST model is that it estimates the derivatives (partial effects) of very general nonlinear models, providing more interpretation about the mapping between the covariates and the dependent variable than other tree based models, such as Random Forests. We provide some asymptotic theory that shows consistency of the partial derivative estimates and we present some examples on both simulated and real data.