The Fault in Our Recommendations: On the Perils of Optimizing the Measurable

Recommendation systems are widespread, and through customized recommendations, promise to match users with options they will like. To that end, data on engagement is collected and used. Most recommendation systems are ranking-based, where they rank and recommend items based on their predicted engagement. However, the engagement signals are often only a crude proxy for utility, as data on the latter is rarely collected or available. This paper explores the following question: By optimizing for measurable proxies, are recommendation systems at risk of significantly under-delivering on utility? If so, how can one improve utility which is seldom measured? To study these questions, we introduce a model of repeated user consumption in which, at each interaction, users select between an outside option and the best option from a recommendation set. Our model accounts for user heterogeneity, with the majority preferring ``popular'' content, and a minority favoring ``niche'' content. The system initially lacks knowledge of individual user preferences but can learn them through observations of users' choices over time. Our theoretical and numerical analysis demonstrate that optimizing for engagement can lead to significant utility losses. Instead, we propose a utility-aware policy that initially recommends a mix of popular and niche content. As the platform becomes more forward-looking, our utility-aware policy achieves the best of both worlds: near-optimal utility and near-optimal engagement simultaneously. Our study elucidates an important feature of recommendation systems; given the ability to suggest multiple items, one can perform significant exploration without incurring significant reductions in engagement. By recommending high-risk, high-reward items alongside popular items, systems can enhance discovery of high utility items without significantly affecting engagement.

Quality vs. Quantity of Data in Contextual Decision-Making: Exact Analysis under Newsvendor Loss

When building datasets, one needs to invest time, money and energy to either aggregate more data or to improve their quality. The most common practice favors quantity over quality without necessarily quantifying the trade-off that emerges. In this work, we study data-driven contextual decision-making and the performance implications of quality and quantity of data. We focus on contextual decision-making with a Newsvendor loss. This loss is that of a central capacity planning problem in Operations Research, but also that associated with quantile regression. We consider a model in which outcomes observed in similar contexts have similar distributions and analyze the performance of a classical class of kernel policies which weigh data according to their similarity in a contextual space. We develop a series of results that lead to an exact characterization of the worst-case expected regret of these policies. This exact characterization applies to any sample size and any observed contexts. The model we develop is flexible, and captures the case of partially observed contexts. This exact analysis enables to unveil new structural insights on the learning behavior of uniform kernel methods: i) the specialized analysis leads to very large improvements in quantification of performance compared to state of the art general purpose bounds. ii) we show an important non-monotonicity of the performance as a function of data size not captured by previous bounds; and iii) we show that in some regimes, a little increase in the quality of the data can dramatically reduce the amount of samples required to reach a performance target. All in all, our work demonstrates that it is possible to quantify in a precise fashion the interplay of data quality and quantity, and performance in a central problem class. It also highlights the need for problem specific bounds in order to understand the trade-offs at play.

Beyond IID: data-driven decision-making in heterogeneous environments

In this work, we study data-driven decision-making and depart from the classical identically and independently distributed (i.i.d.) assumption. We present a new framework in which historical samples are generated from unknown and different distributions, which we dub heterogeneous environments. These distributions are assumed to lie in a heterogeneity ball with known radius and centered around the (also) unknown future (out-of-sample) distribution on which the performance of a decision will be evaluated. We quantify the asymptotic worst-case regret that is achievable by central data-driven policies such as Sample Average Approximation, but also by rate-optimal ones, as a function of the radius of the heterogeneity ball. Our work shows that the type of achievable performance varies considerably across different combinations of problem classes and notions of heterogeneity. We demonstrate the versatility of our framework by comparing achievable guarantees for the heterogeneous version of widely studied data-driven problems such as pricing, ski-rental, and newsvendor. En route, we establish a new connection between data-driven decision-making and distributionally robust optimization.

Contextual Inverse Optimization: Offline and Online Learning

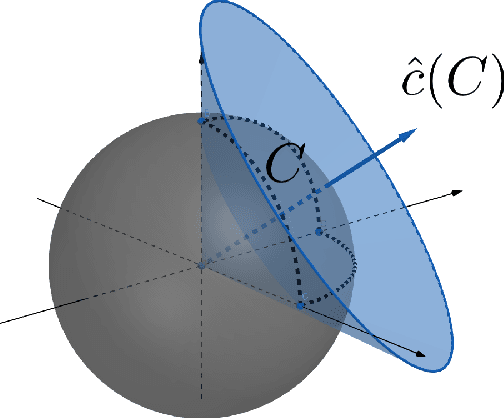
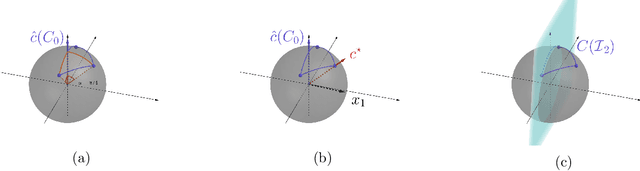
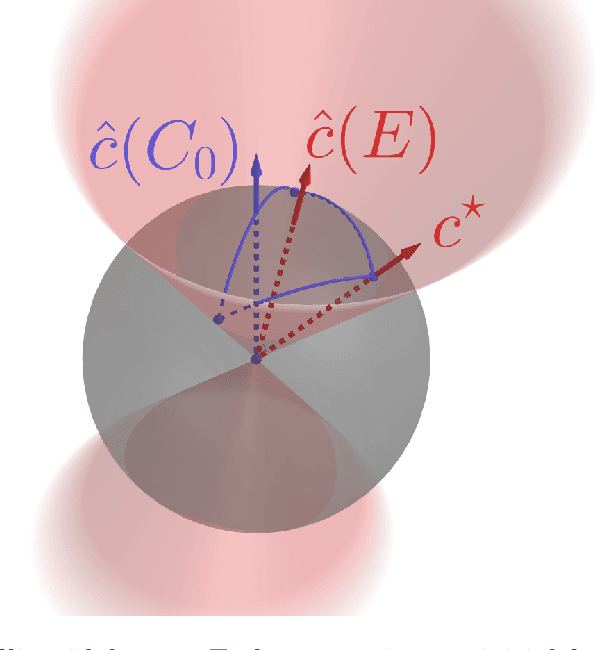
We study the problems of offline and online contextual optimization with feedback information, where instead of observing the loss, we observe, after-the-fact, the optimal action an oracle with full knowledge of the objective function would have taken. We aim to minimize regret, which is defined as the difference between our losses and the ones incurred by an all-knowing oracle. In the offline setting, the decision-maker has information available from past periods and needs to make one decision, while in the online setting, the decision-maker optimizes decisions dynamically over time based a new set of feasible actions and contextual functions in each period. For the offline setting, we characterize the optimal minimax policy, establishing the performance that can be achieved as a function of the underlying geometry of the information induced by the data. In the online setting, we leverage this geometric characterization to optimize the cumulative regret. We develop an algorithm that yields the first regret bound for this problem that is logarithmic in the time horizon.

Optimal Exploration-Exploitation in a Multi-Armed-Bandit Problem with Non-stationary Rewards

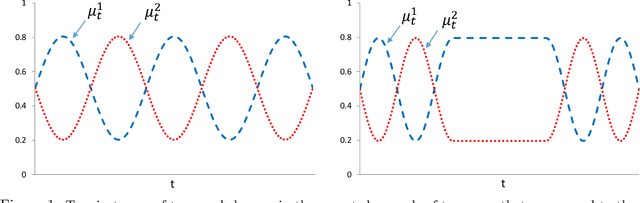
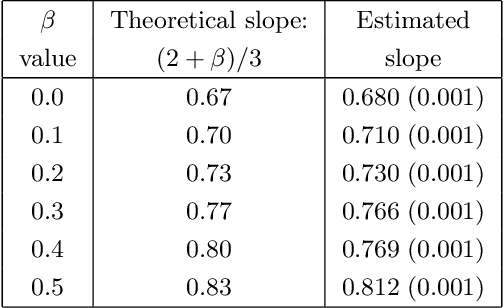
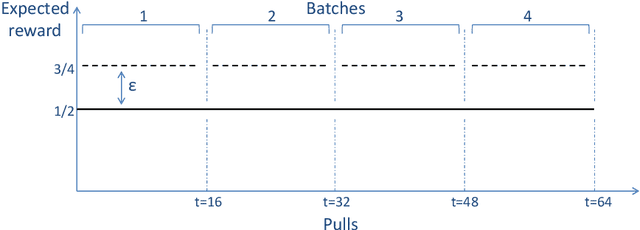
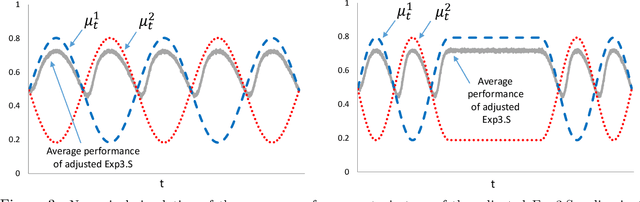
In a multi-armed bandit (MAB) problem a gambler needs to choose at each round of play one of K arms, each characterized by an unknown reward distribution. Reward realizations are only observed when an arm is selected, and the gambler's objective is to maximize his cumulative expected earnings over some given horizon of play T. To do this, the gambler needs to acquire information about arms (exploration) while simultaneously optimizing immediate rewards (exploitation); the price paid due to this trade off is often referred to as the regret, and the main question is how small can this price be as a function of the horizon length T. This problem has been studied extensively when the reward distributions do not change over time; an assumption that supports a sharp characterization of the regret, yet is often violated in practical settings. In this paper, we focus on a MAB formulation which allows for a broad range of temporal uncertainties in the rewards, while still maintaining mathematical tractability. We fully characterize the (regret) complexity of this class of MAB problems by establishing a direct link between the extent of allowable reward "variation" and the minimal achievable regret. Our analysis draws some connections between two rather disparate strands of literature: the adversarial and the stochastic MAB frameworks.