Fair Secretaries with Unfair Predictions

Algorithms with predictions is a recent framework for decision-making under uncertainty that leverages the power of machine-learned predictions without making any assumption about their quality. The goal in this framework is for algorithms to achieve an improved performance when the predictions are accurate while maintaining acceptable guarantees when the predictions are erroneous. A serious concern with algorithms that use predictions is that these predictions can be biased and, as a result, cause the algorithm to make decisions that are deemed unfair. We show that this concern manifests itself in the classical secretary problem in the learning-augmented setting -- the state-of-the-art algorithm can have zero probability of accepting the best candidate, which we deem unfair, despite promising to accept a candidate whose expected value is at least $\max\{\Omega (1) , 1 - O(\epsilon)\}$ times the optimal value, where $\epsilon$ is the prediction error. We show how to preserve this promise while also guaranteeing to accept the best candidate with probability $\Omega(1)$. Our algorithm and analysis are based on a new "pegging" idea that diverges from existing works and simplifies/unifies some of their results. Finally, we extend to the $k$-secretary problem and complement our theoretical analysis with experiments.

Survey of Data-driven Newsvendor: Unified Analysis and Spectrum of Achievable Regrets

In the Newsvendor problem, the goal is to guess the number that will be drawn from some distribution, with asymmetric consequences for guessing too high vs. too low. In the data-driven version, the distribution is unknown, and one must work with samples from the distribution. Data-driven Newsvendor has been studied under many variants: additive vs. multiplicative regret, high probability vs. expectation bounds, and different distribution classes. This paper studies all combinations of these variants, filling in many gaps in the literature and simplifying many proofs. In particular, we provide a unified analysis based on the notion of clustered distributions, which in conjunction with our new lower bounds, shows that the entire spectrum of regrets between $1/\sqrt{n}$ and $1/n$ can be possible.

VC Theory for Inventory Policies

Advances in computational power and AI have increased interest in reinforcement learning approaches to inventory management. This paper provides a theoretical foundation for these approaches and investigates the benefits of restricting to policy structures that are well-established by decades of inventory theory. In particular, we prove generalization guarantees for learning several well-known classes of inventory policies, including base-stock and (s, S) policies, by leveraging the celebrated Vapnik-Chervonenkis (VC) theory. We apply the concepts of the Pseudo-dimension and Fat-shattering dimension from VC theory to determine the generalizability of inventory policies, that is, the difference between an inventory policy's performance on training data and its expected performance on unseen data. We focus on a classical setting without contexts, but allow for an arbitrary distribution over demand sequences and do not make any assumptions such as independence over time. We corroborate our supervised learning results using numerical simulations. Managerially, our theory and simulations translate to the following insights. First, there is a principle of "learning less is more" in inventory management: depending on the amount of data available, it may be beneficial to restrict oneself to a simpler, albeit suboptimal, class of inventory policies to minimize overfitting errors. Second, the number of parameters in a policy class may not be the correct measure of overfitting error: in fact, the class of policies defined by T time-varying base-stock levels exhibits a generalization error comparable to that of the two-parameter (s, S) policy class. Finally, our research suggests situations in which it could be beneficial to incorporate the concepts of base-stock and inventory position into black-box learning machines, instead of having these machines directly learn the order quantity actions.

Quality vs. Quantity of Data in Contextual Decision-Making: Exact Analysis under Newsvendor Loss

When building datasets, one needs to invest time, money and energy to either aggregate more data or to improve their quality. The most common practice favors quantity over quality without necessarily quantifying the trade-off that emerges. In this work, we study data-driven contextual decision-making and the performance implications of quality and quantity of data. We focus on contextual decision-making with a Newsvendor loss. This loss is that of a central capacity planning problem in Operations Research, but also that associated with quantile regression. We consider a model in which outcomes observed in similar contexts have similar distributions and analyze the performance of a classical class of kernel policies which weigh data according to their similarity in a contextual space. We develop a series of results that lead to an exact characterization of the worst-case expected regret of these policies. This exact characterization applies to any sample size and any observed contexts. The model we develop is flexible, and captures the case of partially observed contexts. This exact analysis enables to unveil new structural insights on the learning behavior of uniform kernel methods: i) the specialized analysis leads to very large improvements in quantification of performance compared to state of the art general purpose bounds. ii) we show an important non-monotonicity of the performance as a function of data size not captured by previous bounds; and iii) we show that in some regimes, a little increase in the quality of the data can dramatically reduce the amount of samples required to reach a performance target. All in all, our work demonstrates that it is possible to quantify in a precise fashion the interplay of data quality and quantity, and performance in a central problem class. It also highlights the need for problem specific bounds in order to understand the trade-offs at play.

Degeneracy is OK: Logarithmic Regret for Network Revenue Management with Indiscrete Distributions

We study the classical Network Revenue Management (NRM) problem with accept/reject decisions and $T$ IID arrivals. We consider a distributional form where each arrival must fall under a finite number of possible categories, each with a deterministic resource consumption vector, but a random value distributed continuously over an interval. We develop an online algorithm that achieves $O(\log^2 T)$ regret under this model, with no further assumptions. We develop another online algorithm that achieves an improved $O(\log T)$ regret, with only a second-order growth assumption. To our knowledge, these are the first results achieving logarithmic-level regret in a continuous-distribution NRM model without further ``non-degeneracy'' assumptions. Our results are achieved via new techniques including: a new method of bounding myopic regret, a ``semi-fluid'' relaxation of the offline allocation, and an improved bound on the ``dual convergence''.

Beyond IID: data-driven decision-making in heterogeneous environments

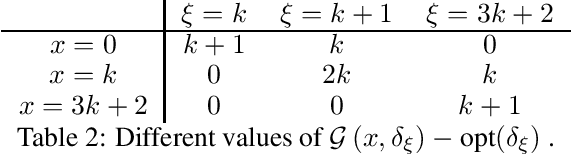
In this work, we study data-driven decision-making and depart from the classical identically and independently distributed (i.i.d.) assumption. We present a new framework in which historical samples are generated from unknown and different distributions, which we dub heterogeneous environments. These distributions are assumed to lie in a heterogeneity ball with known radius and centered around the (also) unknown future (out-of-sample) distribution on which the performance of a decision will be evaluated. We quantify the asymptotic worst-case regret that is achievable by central data-driven policies such as Sample Average Approximation, but also by rate-optimal ones, as a function of the radius of the heterogeneity ball. Our work shows that the type of achievable performance varies considerably across different combinations of problem classes and notions of heterogeneity. We demonstrate the versatility of our framework by comparing achievable guarantees for the heterogeneous version of widely studied data-driven problems such as pricing, ski-rental, and newsvendor. En route, we establish a new connection between data-driven decision-making and distributionally robust optimization.

Fairness Maximization among Offline Agents in Online-Matching Markets

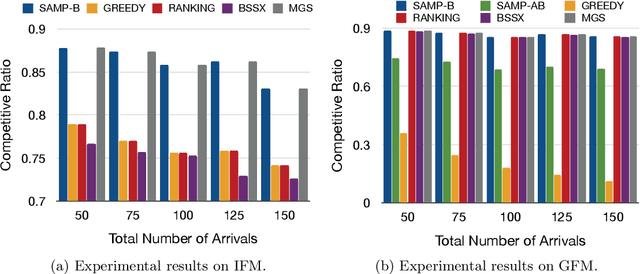
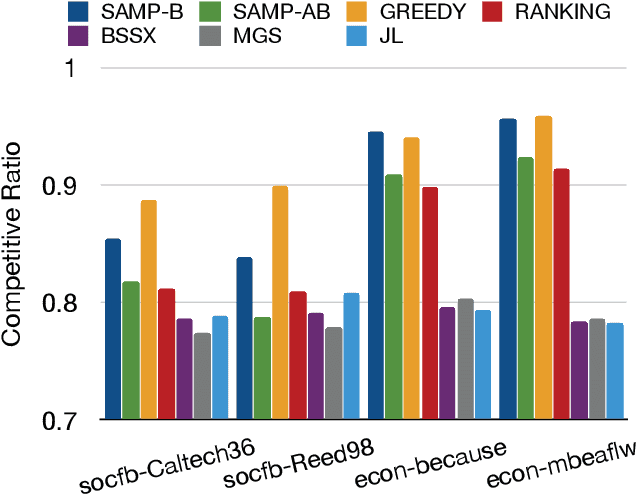
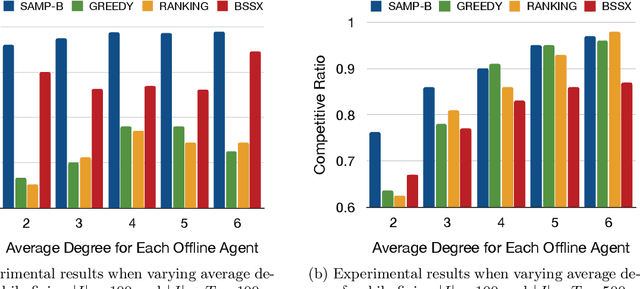
Matching markets involve heterogeneous agents (typically from two parties) who are paired for mutual benefit. During the last decade, matching markets have emerged and grown rapidly through the medium of the Internet. They have evolved into a new format, called Online Matching Markets (OMMs), with examples ranging from crowdsourcing to online recommendations to ridesharing. There are two features distinguishing OMMs from traditional matching markets. One is the dynamic arrival of one side of the market: we refer to these as online agents while the rest are offline agents. Examples of online and offline agents include keywords (online) and sponsors (offline) in Google Advertising; workers (online) and tasks (offline) in Amazon Mechanical Turk (AMT); riders (online) and drivers (offline when restricted to a short time window) in ridesharing. The second distinguishing feature of OMMs is the real-time decision-making element. However, studies have shown that the algorithms making decisions in these OMMs leave disparities in the match rates of offline agents. For example, tasks in neighborhoods of low socioeconomic status rarely get matched to gig workers, and drivers of certain races/genders get discriminated against in matchmaking. In this paper, we propose online matching algorithms which optimize for either individual or group-level fairness among offline agents in OMMs. We present two linear-programming (LP) based sampling algorithms, which achieve online competitive ratios at least 0.725 for individual fairness maximization (IFM) and 0.719 for group fairness maximization (GFM), respectively. We conduct extensive numerical experiments and results show that our boosted version of sampling algorithms are not only conceptually easy to implement but also highly effective in practical instances of fairness-maximization-related models.

The Convex Relaxation Barrier, Revisited: Tightened Single-Neuron Relaxations for Neural Network Verification

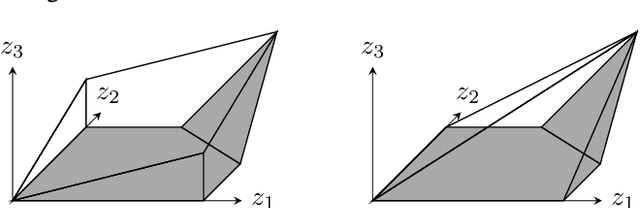
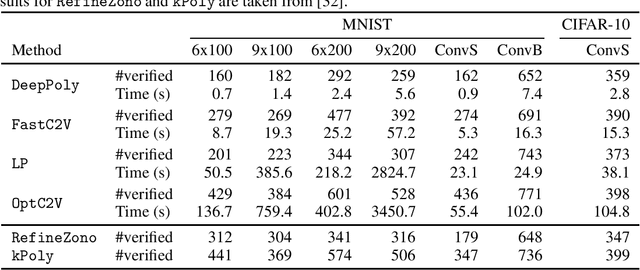
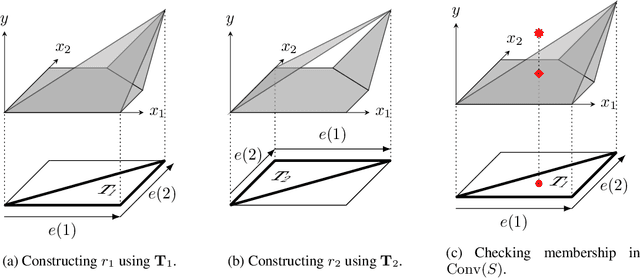
We improve the effectiveness of propagation- and linear-optimization-based neural network verification algorithms with a new tightened convex relaxation for ReLU neurons. Unlike previous single-neuron relaxations which focus only on the univariate input space of the ReLU, our method considers the multivariate input space of the affine pre-activation function preceding the ReLU. Using results from submodularity and convex geometry, we derive an explicit description of the tightest possible convex relaxation when this multivariate input is over a box domain. We show that our convex relaxation is significantly stronger than the commonly used univariate-input relaxation which has been proposed as a natural convex relaxation barrier for verification. While our description of the relaxation may require an exponential number of inequalities, we show that they can be separated in linear time and hence can be efficiently incorporated into optimization algorithms on an as-needed basis. Based on this novel relaxation, we design two polynomial-time algorithms for neural network verification: a linear-programming-based algorithm that leverages the full power of our relaxation, and a fast propagation algorithm that generalizes existing approaches. In both cases, we show that for a modest increase in computational effort, our strengthened relaxation enables us to verify a significantly larger number of instances compared to similar algorithms.

Inventory Balancing with Online Learning

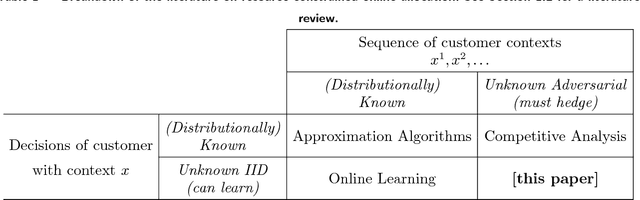
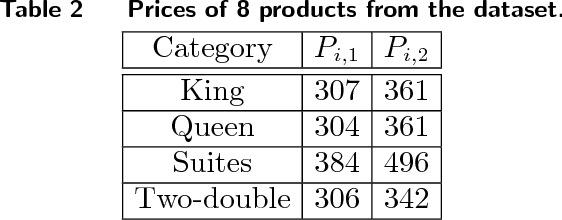
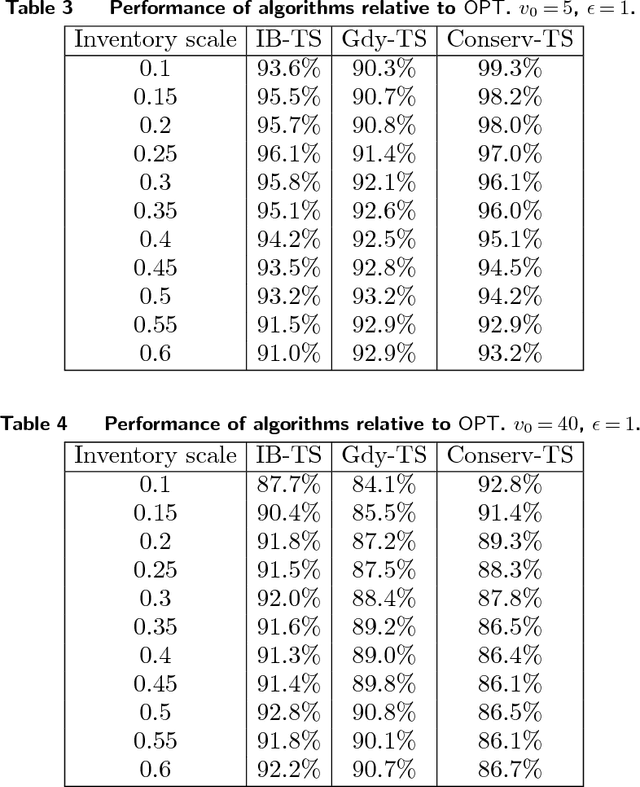
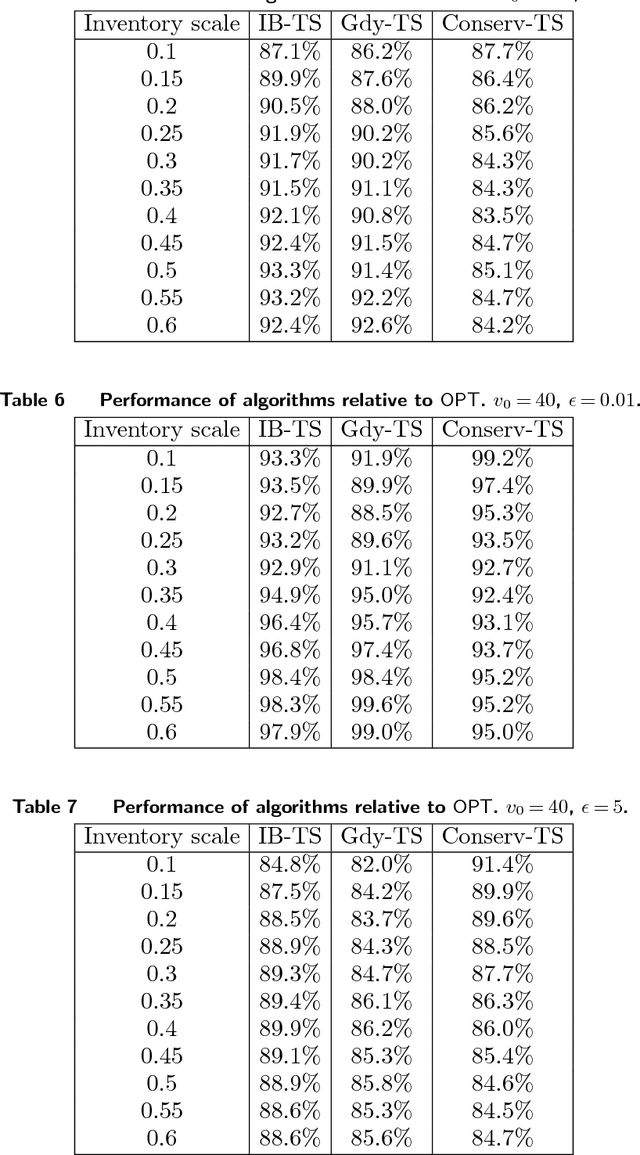
We study a general problem of allocating limited resources to heterogeneous customers over time under model uncertainty. Each type of customer can be serviced using different actions, each of which stochastically consumes some combination of resources, and returns different rewards for the resources consumed. We consider a general model where the resource consumption distribution associated with each (customer type, action)-combination is not known, but is consistent and can be learned over time. In addition, the sequence of customer types to arrive over time is arbitrary and completely unknown. We overcome both the challenges of model uncertainty and customer heterogeneity by judiciously synthesizing two algorithmic frameworks from the literature: inventory balancing, which "reserves" a portion of each resource for high-reward customer types which could later arrive, and online learning, which shows how to "explore" the resource consumption distributions of each customer type under different actions. We define an auxiliary problem, which allows for existing competitive ratio and regret bounds to be seamlessly integrated. Furthermore, we show that the performance guarantee generated by our framework is tight, that is, we provide an information-theoretic lower bound which shows that both the loss from competitive ratio and the loss for regret are relevant in the combined problem. Finally, we demonstrate the efficacy of our algorithms on a publicly available hotel data set. Our framework is highly practical in that it requires no historical data (no fitted customer choice models, nor forecasting of customer arrival patterns) and can be used to initialize allocation strategies in fast-changing environments.