Policy Regularized Distributionally Robust Markov Decision Processes with Linear Function Approximation

Decision-making under distribution shift is a central challenge in reinforcement learning (RL), where training and deployment environments differ. We study this problem through the lens of robust Markov decision processes (RMDPs), which optimize performance against adversarial transition dynamics. Our focus is the online setting, where the agent has only limited interaction with the environment, making sample efficiency and exploration especially critical. Policy optimization, despite its success in standard RL, remains theoretically and empirically underexplored in robust RL. To bridge this gap, we propose \textbf{D}istributionally \textbf{R}obust \textbf{R}egularized \textbf{P}olicy \textbf{O}ptimization algorithm (DR-RPO), a model-free online policy optimization method that learns robust policies with sublinear regret. To enable tractable optimization within the softmax policy class, DR-RPO incorporates reference-policy regularization, yielding RMDP variants that are doubly constrained in both transitions and policies. To scale to large state-action spaces, we adopt the $d$-rectangular linear MDP formulation and combine linear function approximation with an upper confidence bonus for optimistic exploration. We provide theoretical guarantees showing that policy optimization can achieve polynomial suboptimality bounds and sample efficiency in robust RL, matching the performance of value-based approaches. Finally, empirical results across diverse domains corroborate our theory and demonstrate the robustness of DR-RPO.

Rethinking Langevin Thompson Sampling from A Stochastic Approximation Perspective

Most existing approximate Thompson Sampling (TS) algorithms for multi-armed bandits use Stochastic Gradient Langevin Dynamics (SGLD) or its variants in each round to sample from the posterior, relaxing the need for conjugacy assumptions between priors and reward distributions in vanilla TS. However, they often require approximating a different posterior distribution in different round of the bandit problem. This requires tricky, round-specific tuning of hyperparameters such as dynamic learning rates, causing challenges in both theoretical analysis and practical implementation. To alleviate this non-stationarity, we introduce TS-SA, which incorporates stochastic approximation (SA) within the TS framework. In each round, TS-SA constructs a posterior approximation only using the most recent reward(s), performs a Langevin Monte Carlo (LMC) update, and applies an SA step to average noisy proposals over time. This can be interpreted as approximating a stationary posterior target throughout the entire algorithm, which further yields a fixed step-size, a unified convergence analysis framework, and improved posterior estimates through temporal averaging. We establish near-optimal regret bounds for TS-SA, with a simplified and more intuitive theoretical analysis enabled by interpreting the entire algorithm as a simulation of a stationary SGLD process. Our empirical results demonstrate that even a single-step Langevin update with certain warm-up outperforms existing methods substantially on bandit tasks.

MOBODY: Model Based Off-Dynamics Offline Reinforcement Learning

We study the off-dynamics offline reinforcement learning problem, where the goal is to learn a policy from offline datasets collected from source and target domains with mismatched transition. Existing off-dynamics offline RL methods typically either filter source transitions that resemble those of the target domain or apply reward augmentation to source data, both constrained by the limited transitions available from the target domain. As a result, the learned policy is unable to explore target domain beyond the offline datasets. We propose MOBODY, a Model-Based Off-Dynamics offline RL algorithm that addresses this limitation by enabling exploration of the target domain via learned dynamics. MOBODY generates new synthetic transitions in the target domain through model rollouts, which are used as data augmentation during offline policy learning. Unlike existing model-based methods that learn dynamics from a single domain, MOBODY tackles the challenge of mismatched dynamics by leveraging both source and target datasets. Directly merging these datasets can bias the learned model toward source dynamics. Instead, MOBODY learns target dynamics by discovering a shared latent representation of states and transitions across domains through representation learning. To stabilize training, MOBODY incorporates a behavior cloning loss that regularizes the policy. Specifically, we introduce a Q-weighted behavior cloning loss that regularizes the policy toward actions with high target-domain Q-values, rather than uniformly imitating all actions in the dataset. These Q-values are learned from an enhanced target dataset composed of offline target data, augmented source data, and rollout data from the learned target dynamics. We evaluate MOBODY on MuJoCo benchmarks and show that it significantly outperforms state-of-the-art baselines, with especially pronounced improvements in challenging scenarios.

How to Provably Improve Return Conditioned Supervised Learning?

In sequential decision-making problems, Return-Conditioned Supervised Learning (RCSL) has gained increasing recognition for its simplicity and stability in modern decision-making tasks. Unlike traditional offline reinforcement learning (RL) algorithms, RCSL frames policy learning as a supervised learning problem by taking both the state and return as input. This approach eliminates the instability often associated with temporal difference (TD) learning in offline RL. However, RCSL has been criticized for lacking the stitching property, meaning its performance is inherently limited by the quality of the policy used to generate the offline dataset. To address this limitation, we propose a principled and simple framework called Reinforced RCSL. The key innovation of our framework is the introduction of a concept we call the in-distribution optimal return-to-go. This mechanism leverages our policy to identify the best achievable in-dataset future return based on the current state, avoiding the need for complex return augmentation techniques. Our theoretical analysis demonstrates that Reinforced RCSL can consistently outperform the standard RCSL approach. Empirical results further validate our claims, showing significant performance improvements across a range of benchmarks.

Linear Mixture Distributionally Robust Markov Decision Processes

Many real-world decision-making problems face the off-dynamics challenge: the agent learns a policy in a source domain and deploys it in a target domain with different state transitions. The distributionally robust Markov decision process (DRMDP) addresses this challenge by finding a robust policy that performs well under the worst-case environment within a pre-specified uncertainty set of transition dynamics. Its effectiveness heavily hinges on the proper design of these uncertainty sets, based on prior knowledge of the dynamics. In this work, we propose a novel linear mixture DRMDP framework, where the nominal dynamics is assumed to be a linear mixture model. In contrast with existing uncertainty sets directly defined as a ball centered around the nominal kernel, linear mixture DRMDPs define the uncertainty sets based on a ball around the mixture weighting parameter. We show that this new framework provides a more refined representation of uncertainties compared to conventional models based on $(s,a)$-rectangularity and $d$-rectangularity, when prior knowledge about the mixture model is present. We propose a meta algorithm for robust policy learning in linear mixture DRMDPs with general $f$-divergence defined uncertainty sets, and analyze its sample complexities under three divergence metrics instantiations: total variation, Kullback-Leibler, and $\chi^2$ divergences. These results establish the statistical learnability of linear mixture DRMDPs, laying the theoretical foundation for future research on this new setting.

Off-Dynamics Reinforcement Learning via Domain Adaptation and Reward Augmented Imitation

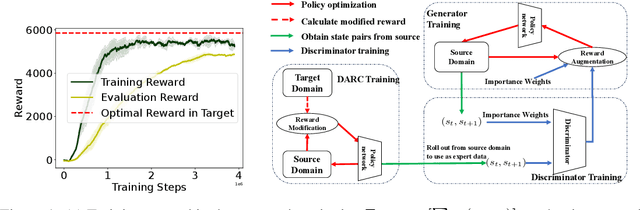
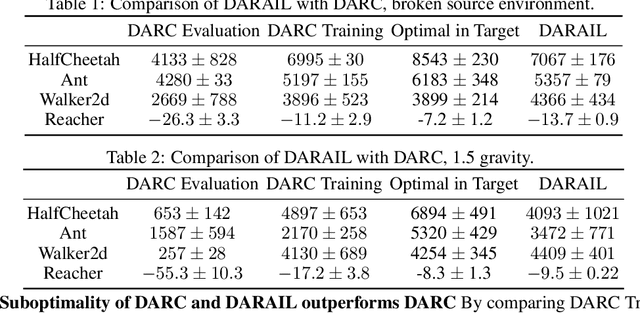
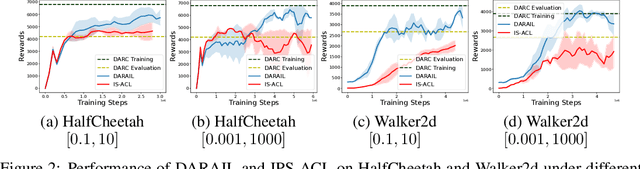
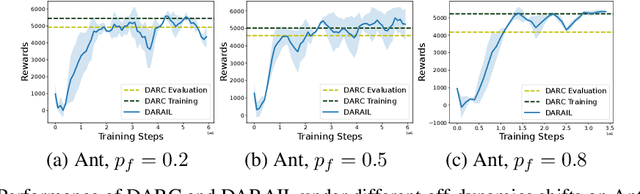
Training a policy in a source domain for deployment in the target domain under a dynamics shift can be challenging, often resulting in performance degradation. Previous work tackles this challenge by training on the source domain with modified rewards derived by matching distributions between the source and the target optimal trajectories. However, pure modified rewards only ensure the behavior of the learned policy in the source domain resembles trajectories produced by the target optimal policies, which does not guarantee optimal performance when the learned policy is actually deployed to the target domain. In this work, we propose to utilize imitation learning to transfer the policy learned from the reward modification to the target domain so that the new policy can generate the same trajectories in the target domain. Our approach, Domain Adaptation and Reward Augmented Imitation Learning (DARAIL), utilizes the reward modification for domain adaptation and follows the general framework of generative adversarial imitation learning from observation (GAIfO) by applying a reward augmented estimator for the policy optimization step. Theoretically, we present an error bound for our method under a mild assumption regarding the dynamics shift to justify the motivation of our method. Empirically, our method outperforms the pure modified reward method without imitation learning and also outperforms other baselines in benchmark off-dynamics environments.

Return Augmented Decision Transformer for Off-Dynamics Reinforcement Learning

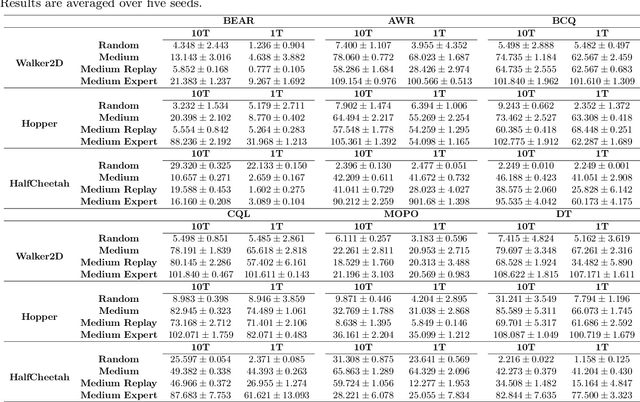
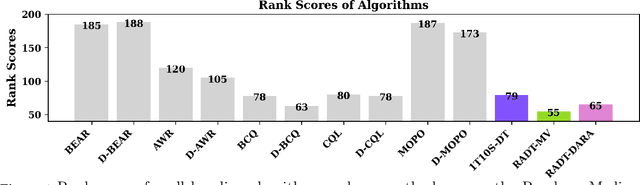
We study offline off-dynamics reinforcement learning (RL) to utilize data from an easily accessible source domain to enhance policy learning in a target domain with limited data. Our approach centers on return-conditioned supervised learning (RCSL), particularly focusing on the decision transformer (DT), which can predict actions conditioned on desired return guidance and complete trajectory history. Previous works tackle the dynamics shift problem by augmenting the reward in the trajectory from the source domain to match the optimal trajectory in the target domain. However, this strategy can not be directly applicable in RCSL owing to (1) the unique form of the RCSL policy class, which explicitly depends on the return, and (2) the absence of a straightforward representation of the optimal trajectory distribution. We propose the Return Augmented Decision Transformer (RADT) method, where we augment the return in the source domain by aligning its distribution with that in the target domain. We provide the theoretical analysis demonstrating that the RCSL policy learned from RADT achieves the same level of suboptimality as would be obtained without a dynamics shift. We introduce two practical implementations RADT-DARA and RADT-MV respectively. Extensive experiments conducted on D4RL datasets reveal that our methods generally outperform dynamic programming based methods in off-dynamics RL scenarios.

Upper and Lower Bounds for Distributionally Robust Off-Dynamics Reinforcement Learning

We study off-dynamics Reinforcement Learning (RL), where the policy training and deployment environments are different. To deal with this environmental perturbation, we focus on learning policies robust to uncertainties in transition dynamics under the framework of distributionally robust Markov decision processes (DRMDPs), where the nominal and perturbed dynamics are linear Markov Decision Processes. We propose a novel algorithm We-DRIVE-U that enjoys an average suboptimality $\widetilde{\mathcal{O}}\big({d H \cdot \min \{1/{\rho}, H\}/\sqrt{K} }\big)$, where $K$ is the number of episodes, $H$ is the horizon length, $d$ is the feature dimension and $\rho$ is the uncertainty level. This result improves the state-of-the-art by $\mathcal{O}(dH/\min\{1/\rho,H\})$. We also construct a novel hard instance and derive the first information-theoretic lower bound in this setting, which indicates our algorithm is near-optimal up to $\mathcal{O}(\sqrt{H})$ for any uncertainty level $\rho\in(0,1]$. Our algorithm also enjoys a 'rare-switching' design, and thus only requires $\mathcal{O}(dH\log(1+H^2K))$ policy switches and $\mathcal{O}(d^2H\log(1+H^2K))$ calls for oracle to solve dual optimization problems, which significantly improves the computational efficiency of existing algorithms for DRMDPs, whose policy switch and oracle complexities are both $\mathcal{O}(K)$.

Pre-trained Language Models Improve the Few-shot Prompt Ability of Decision Transformer

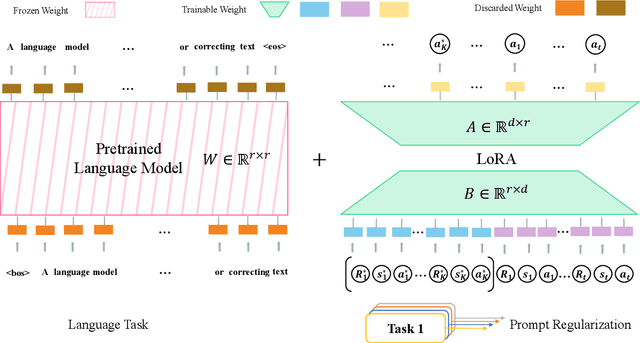
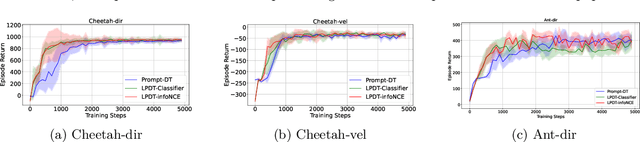
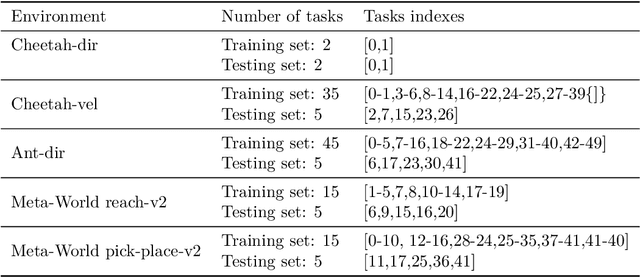
Decision Transformer (DT) has emerged as a promising class of algorithms in offline reinforcement learning (RL) tasks, leveraging pre-collected datasets and Transformer's capability to model long sequences. Recent works have demonstrated that using parts of trajectories from training tasks as prompts in DT enhances its performance on unseen tasks, giving rise to Prompt-DT methods. However, collecting data from specific environments can be both costly and unsafe in many scenarios, leading to suboptimal performance and limited few-shot prompt abilities due to the data-hungry nature of Transformer-based models. Additionally, the limited datasets used in pre-training make it challenging for Prompt-DT type of methods to distinguish between various RL tasks through prompts alone. To address these challenges, we introduce the Language model-initialized Prompt Decision Transformer (LPDT), which leverages pre-trained language models for meta-RL tasks and fine-tunes the model using Low-rank Adaptation (LoRA). We further incorporate prompt regularization to effectively differentiate between tasks based on prompt feature representations. Our approach integrates pre-trained language model and RL tasks seamlessly. Extensive empirical studies demonstrate that initializing with a pre-trained language model significantly enhances the performance of Prompt-DT on unseen tasks compared to baseline methods.

More Efficient Randomized Exploration for Reinforcement Learning via Approximate Sampling

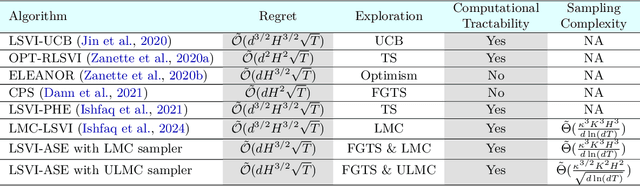
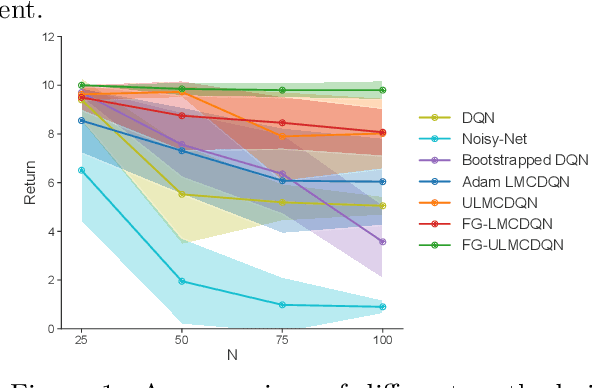
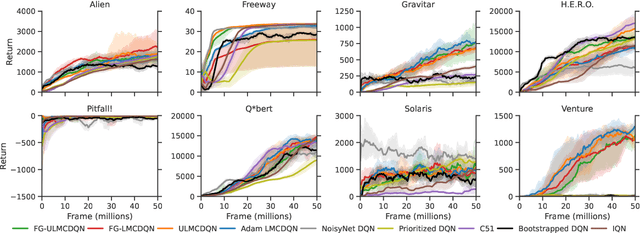
Thompson sampling (TS) is one of the most popular exploration techniques in reinforcement learning (RL). However, most TS algorithms with theoretical guarantees are difficult to implement and not generalizable to Deep RL. While the emerging approximate sampling-based exploration schemes are promising, most existing algorithms are specific to linear Markov Decision Processes (MDP) with suboptimal regret bounds, or only use the most basic samplers such as Langevin Monte Carlo. In this work, we propose an algorithmic framework that incorporates different approximate sampling methods with the recently proposed Feel-Good Thompson Sampling (FGTS) approach (Zhang, 2022; Dann et al., 2021), which was previously known to be computationally intractable in general. When applied to linear MDPs, our regret analysis yields the best known dependency of regret on dimensionality, surpassing existing randomized algorithms. Additionally, we provide explicit sampling complexity for each employed sampler. Empirically, we show that in tasks where deep exploration is necessary, our proposed algorithms that combine FGTS and approximate sampling perform significantly better compared to other strong baselines. On several challenging games from the Atari 57 suite, our algorithms achieve performance that is either better than or on par with other strong baselines from the deep RL literature.