Anatomical Region-Guided Contrastive Decoding: A Plug-and-Play Strategy for Mitigating Hallucinations in Medical VLMs

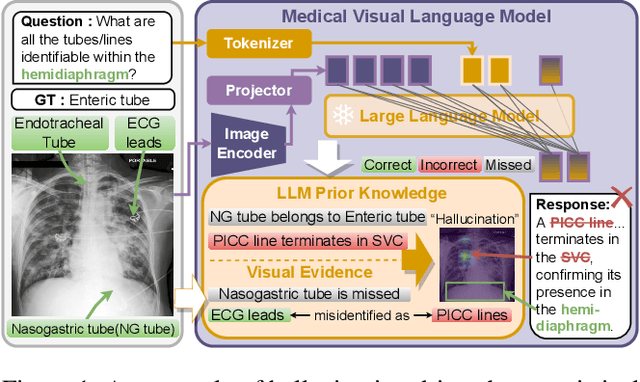
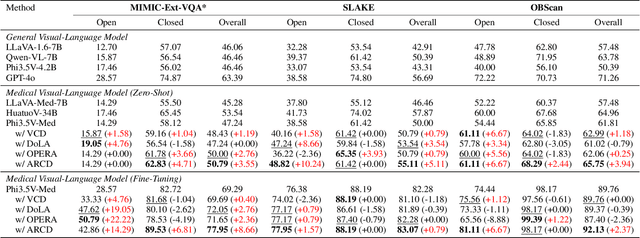
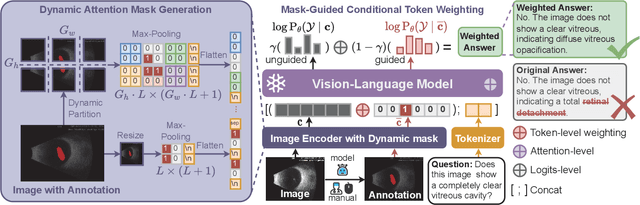
Medical Vision-Language Models (MedVLMs) show immense promise in clinical applicability. However, their reliability is hindered by hallucinations, where models often fail to derive answers from visual evidence, instead relying on learned textual priors. Existing mitigation strategies for MedVLMs have distinct limitations: training-based methods rely on costly expert annotations, limiting scalability, while training-free interventions like contrastive decoding, though data-efficient, apply a global, untargeted correction whose effects in complex real-world clinical settings can be unreliable. To address these challenges, we introduce Anatomical Region-Guided Contrastive Decoding (ARCD), a plug-and-play strategy that mitigates hallucinations by providing targeted, region-specific guidance. Our module leverages an anatomical mask to direct a three-tiered contrastive decoding process. By dynamically re-weighting at the token, attention, and logits levels, it verifiably steers the model's focus onto specified regions, reinforcing anatomical understanding and suppressing factually incorrect outputs. Extensive experiments across diverse datasets, including chest X-ray, CT, brain MRI, and ocular ultrasound, demonstrate our method's effectiveness in improving regional understanding, reducing hallucinations, and enhancing overall diagnostic accuracy.

Stabilization of nonlinear systems with unknown delays via delay-adaptive neural operator approximate predictors

This work establishes the first rigorous stability guarantees for approximate predictors in delay-adaptive control of nonlinear systems, addressing a key challenge in practical implementations where exact predictors are unavailable. We analyze two scenarios: (i) when the actuated input is directly measurable, and (ii) when it is estimated online. For the measurable input case, we prove semi-global practical asymptotic stability with an explicit bound proportional to the approximation error $\epsilon$. For the unmeasured input case, we demonstrate local practical asymptotic stability, with the region of attraction explicitly dependent on both the initial delay estimate and the predictor approximation error. To bridge theory and practice, we show that neural operators-a flexible class of neural network-based approximators-can achieve arbitrarily small approximation errors, thus satisfying the conditions of our stability theorems. Numerical experiments on two nonlinear benchmark systems-a biological protein activator/repressor model and a micro-organism growth Chemostat model-validate our theoretical results. In particular, our numerical simulations confirm stability under approximate predictors, highlight the strong generalization capabilities of neural operators, and demonstrate a substantial computational speedup of up to 15x compared to a baseline fixed-point method.

Uncovering the Bigger Picture: Comprehensive Event Understanding Via Diverse News Retrieval

Access to diverse perspectives is essential for understanding real-world events, yet most news retrieval systems prioritize textual relevance, leading to redundant results and limited viewpoint exposure. We propose NEWSCOPE, a two-stage framework for diverse news retrieval that enhances event coverage by explicitly modeling semantic variation at the sentence level. The first stage retrieves topically relevant content using dense retrieval, while the second stage applies sentence-level clustering and diversity-aware re-ranking to surface complementary information. To evaluate retrieval diversity, we introduce three interpretable metrics, namely Average Pairwise Distance, Positive Cluster Coverage, and Information Density Ratio, and construct two paragraph-level benchmarks: LocalNews and DSGlobal. Experiments show that NEWSCOPE consistently outperforms strong baselines, achieving significantly higher diversity without compromising relevance. Our results demonstrate the effectiveness of fine-grained, interpretable modeling in mitigating redundancy and promoting comprehensive event understanding. The data and code are available at https://github.com/tangyixuan/NEWSCOPE.

Data-driven operator learning for energy-efficient building control

Energy-efficient ventilation control plays a vital role in reducing building energy consumption while ensuring occupant health and comfort. While Computational Fluid Dynamics (CFD) simulations offer high-fidelity modeling of airflow for building HVAC design, their high computational cost makes them impractical for practical adoption in real-time building management system. In this work, we present a data-driven framework that combines the physical accuracy of CFD with the computational efficiency of machine learning to enable energy-efficient building ventilation control. Our method jointly optimizes airflow supply rates and vent angles to reduce energy use and adhere to air quality constraints. We train a neural operator transformer to learn the mapping from building control actions to airflow field distributions using high-resolution CFD data. This learned operator enables a gradient-based control framework capable of optimal decision-making. Experimental results demonstrate that our approach achieves substantial energy savings compared to maximum airflow rate control, rule-based control, and data-driven control based on regional average CO2 predictions, while consistently maintaining safe indoor air quality. These results highlight the practicality and scalability of our method for enabling safe and energy-efficient building management.

Analytical Lyapunov Function Discovery: An RL-based Generative Approach

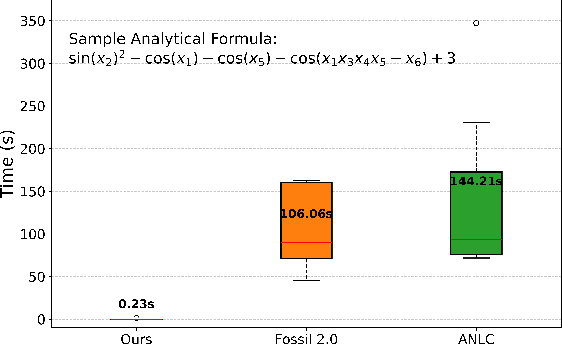
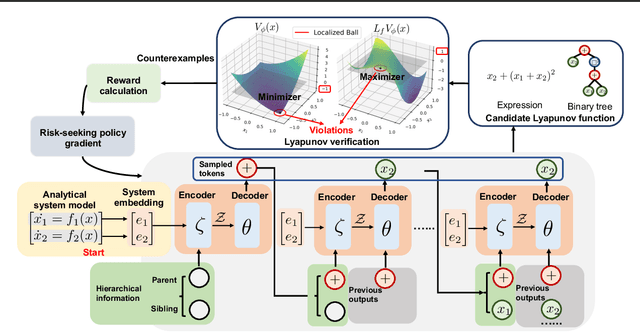
Despite advances in learning-based methods, finding valid Lyapunov functions for nonlinear dynamical systems remains challenging. Current neural network approaches face two main issues: challenges in scalable verification and limited interpretability. To address these, we propose an end-to-end framework using transformers to construct analytical Lyapunov functions (local), which simplifies formal verification, enhances interpretability, and provides valuable insights for control engineers. Our framework consists of a transformer-based trainer that generates candidate Lyapunov functions and a falsifier that verifies candidate expressions and refines the model via risk-seeking policy gradient. Unlike Alfarano et al. (2024), which utilizes pre-training and seeks global Lyapunov functions for low-dimensional systems, our model is trained from scratch via reinforcement learning (RL) and succeeds in finding local Lyapunov functions for high-dimensional and non-polynomial systems. Given the analytical nature of the candidates, we employ efficient optimization methods for falsification during training and formal verification tools for the final verification. We demonstrate the efficiency of our approach on a range of nonlinear dynamical systems with up to ten dimensions and show that it can discover Lyapunov functions not previously identified in the control literature.

Neural Operators for Predictor Feedback Control of Nonlinear Delay Systems

Predictor feedback designs are critical for delay-compensating controllers in nonlinear systems. However, these designs are limited in practical applications as predictors cannot be directly implemented, but require numerical approximation schemes. These numerical schemes, typically combining finite difference and successive approximations, become computationally prohibitive when the dynamics of the system are expensive to compute. To alleviate this issue, we propose approximating the predictor mapping via a neural operator. In particular, we introduce a new perspective on predictor designs by recasting the predictor formulation as an operator learning problem. We then prove the existence of an arbitrarily accurate neural operator approximation of the predictor operator. Under the approximated-predictor, we achieve semiglobal practical stability of the closed-loop nonlinear system. The estimate is semiglobal in a unique sense - namely, one can increase the set of initial states as large as desired but this will naturally increase the difficulty of training a neural operator approximation which appears practically in the stability estimate. Furthermore, we emphasize that our result holds not just for neural operators, but any black-box predictor satisfying a universal approximation error bound. From a computational perspective, the advantage of the neural operator approach is clear as it requires training once, offline and then is deployed with very little computational cost in the feedback controller. We conduct experiments controlling a 5-link robotic manipulator with different state-of-the-art neural operator architectures demonstrating speedups on the magnitude of $10^2$ compared to traditional predictor approximation schemes.

Off-Dynamics Reinforcement Learning via Domain Adaptation and Reward Augmented Imitation

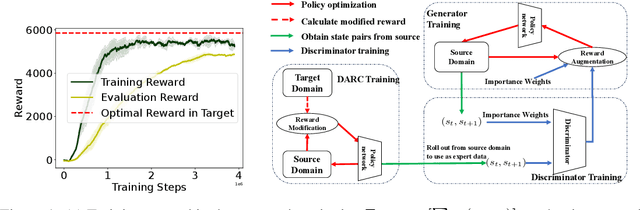
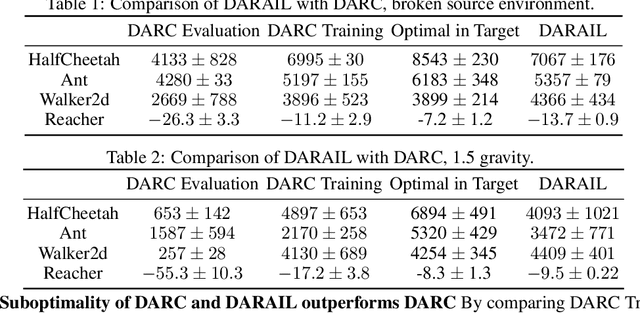
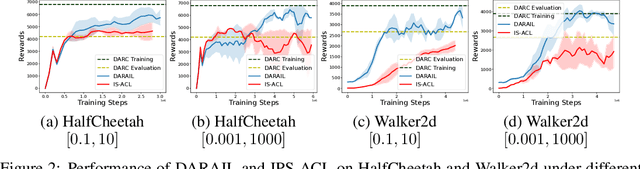
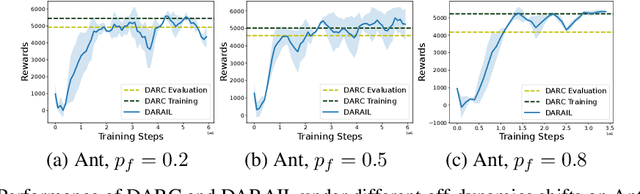
Training a policy in a source domain for deployment in the target domain under a dynamics shift can be challenging, often resulting in performance degradation. Previous work tackles this challenge by training on the source domain with modified rewards derived by matching distributions between the source and the target optimal trajectories. However, pure modified rewards only ensure the behavior of the learned policy in the source domain resembles trajectories produced by the target optimal policies, which does not guarantee optimal performance when the learned policy is actually deployed to the target domain. In this work, we propose to utilize imitation learning to transfer the policy learned from the reward modification to the target domain so that the new policy can generate the same trajectories in the target domain. Our approach, Domain Adaptation and Reward Augmented Imitation Learning (DARAIL), utilizes the reward modification for domain adaptation and follows the general framework of generative adversarial imitation learning from observation (GAIfO) by applying a reward augmented estimator for the policy optimization step. Theoretically, we present an error bound for our method under a mild assumption regarding the dynamics shift to justify the motivation of our method. Empirically, our method outperforms the pure modified reward method without imitation learning and also outperforms other baselines in benchmark off-dynamics environments.

Generalizable Motion Planning via Operator Learning

In this work, we introduce a planning neural operator (PNO) for predicting the value function of a motion planning problem. We recast value function approximation as learning a single operator from the cost function space to the value function space, which is defined by an Eikonal partial differential equation (PDE). Specifically, we recast computing value functions as learning a single operator across continuous function spaces which prove is equivalent to solving an Eikonal PDE. Through this reformulation, our learned PNO is able to generalize to new motion planning problems without retraining. Therefore, our PNO model, despite being trained with a finite number of samples at coarse resolution, inherits the zero-shot super-resolution property of neural operators. We demonstrate accurate value function approximation at 16 times the training resolution on the MovingAI lab's 2D city dataset and compare with state-of-the-art neural value function predictors on 3D scenes from the iGibson building dataset. Lastly, we investigate employing the value function output of PNO as a heuristic function to accelerate motion planning. We show theoretically that the PNO heuristic is $\epsilon$-consistent by introducing an inductive bias layer that guarantees our value functions satisfy the triangle inequality. With our heuristic, we achieve a 30% decrease in nodes visited while obtaining near optimal path lengths on the MovingAI lab 2D city dataset, compared to classical planning methods (A*, RRT*).

Online Event-Triggered Switching for Frequency Control in Power Grids with Variable Inertia

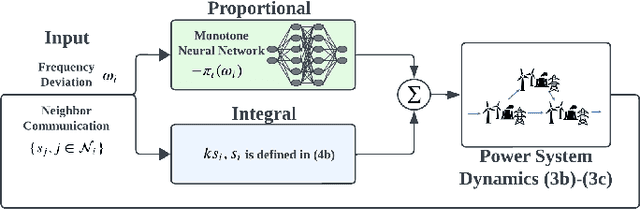
The increasing integration of renewable energy resources into power grids has led to time-varying system inertia and consequent degradation in frequency dynamics. A promising solution to alleviate performance degradation is using power electronics interfaced energy resources, such as renewable generators and battery energy storage for primary frequency control, by adjusting their power output set-points in response to frequency deviations. However, designing a frequency controller under time-varying inertia is challenging. Specifically, the stability or optimality of controllers designed for time-invariant systems can be compromised once applied to a time-varying system. We model the frequency dynamics under time-varying inertia as a nonlinear switching system, where the frequency dynamics under each mode are described by the nonlinear swing equations and different modes represent different inertia levels. We identify a key controller structure, named Neural Proportional-Integral (Neural-PI) controller, that guarantees exponential input-to-state stability for each mode. To further improve performance, we present an online event-triggered switching algorithm to select the most suitable controller from a set of Neural-PI controllers, each optimized for specific inertia levels. Simulations on the IEEE 39-bus system validate the effectiveness of the proposed online switching control method with stability guarantees and optimized performance for frequency control under time-varying inertia.

Adaptive control of reaction-diffusion PDEs via neural operator-approximated gain kernels

Neural operator approximations of the gain kernels in PDE backstepping has emerged as a viable method for implementing controllers in real time. With such an approach, one approximates the gain kernel, which maps the plant coefficient into the solution of a PDE, with a neural operator. It is in adaptive control that the benefit of the neural operator is realized, as the kernel PDE solution needs to be computed online, for every updated estimate of the plant coefficient. We extend the neural operator methodology from adaptive control of a hyperbolic PDE to adaptive control of a benchmark parabolic PDE (a reaction-diffusion equation with a spatially-varying and unknown reaction coefficient). We prove global stability and asymptotic regulation of the plant state for a Lyapunov design of parameter adaptation. The key technical challenge of the result is handling the 2D nature of the gain kernels and proving that the target system with two distinct sources of perturbation terms, due to the parameter estimation error and due to the neural approximation error, is Lyapunov stable. To verify our theoretical result, we present simulations achieving calculation speedups up to 45x relative to the traditional finite difference solvers for every timestep in the simulation trajectory.