Fast and Reliable $N-k$ Contingency Screening with Input-Convex Neural Networks

Power system operators must ensure that dispatch decisions remain feasible in case of grid outages or contingencies to prevent cascading failures and ensure reliable operation. However, checking the feasibility of all $N - k$ contingencies -- every possible simultaneous failure of $k$ grid components -- is computationally intractable for even small $k$, requiring system operators to resort to heuristic screening methods. Because of the increase in uncertainty and changes in system behaviors, heuristic lists might not include all relevant contingencies, generating false negatives in which unsafe scenarios are misclassified as safe. In this work, we propose to use input-convex neural networks (ICNNs) for contingency screening. We show that ICNN reliability can be determined by solving a convex optimization problem, and by scaling model weights using this problem as a differentiable optimization layer during training, we can learn an ICNN classifier that is both data-driven and has provably guaranteed reliability. Namely, our method can ensure a zero false negative rate. We empirically validate this methodology in a case study on the IEEE 39-bus test network, observing that it yields substantial (10-20x) speedups while having excellent classification accuracy.

Online Event-Triggered Switching for Frequency Control in Power Grids with Variable Inertia

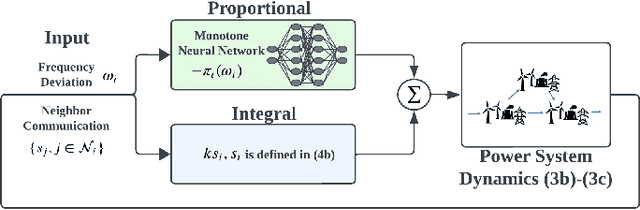
The increasing integration of renewable energy resources into power grids has led to time-varying system inertia and consequent degradation in frequency dynamics. A promising solution to alleviate performance degradation is using power electronics interfaced energy resources, such as renewable generators and battery energy storage for primary frequency control, by adjusting their power output set-points in response to frequency deviations. However, designing a frequency controller under time-varying inertia is challenging. Specifically, the stability or optimality of controllers designed for time-invariant systems can be compromised once applied to a time-varying system. We model the frequency dynamics under time-varying inertia as a nonlinear switching system, where the frequency dynamics under each mode are described by the nonlinear swing equations and different modes represent different inertia levels. We identify a key controller structure, named Neural Proportional-Integral (Neural-PI) controller, that guarantees exponential input-to-state stability for each mode. To further improve performance, we present an online event-triggered switching algorithm to select the most suitable controller from a set of Neural-PI controllers, each optimized for specific inertia levels. Simulations on the IEEE 39-bus system validate the effectiveness of the proposed online switching control method with stability guarantees and optimized performance for frequency control under time-varying inertia.

Efficient Reinforcement Learning Through Trajectory Generation

A key barrier to using reinforcement learning (RL) in many real-world applications is the requirement of a large number of system interactions to learn a good control policy. Off-policy and Offline RL methods have been proposed to reduce the number of interactions with the physical environment by learning control policies from historical data. However, their performances suffer from the lack of exploration and the distributional shifts in trajectories once controllers are updated. Moreover, most RL methods require that all states are directly observed, which is difficult to be attained in many settings. To overcome these challenges, we propose a trajectory generation algorithm, which adaptively generates new trajectories as if the system is being operated and explored under the updated control policies. Motivated by the fundamental lemma for linear systems, assuming sufficient excitation, we generate trajectories from linear combinations of historical trajectories. For linear feedback control, we prove that the algorithm generates trajectories with the exact distribution as if they are sampled from the real system using the updated control policy. In particular, the algorithm extends to systems where the states are not directly observed. Experiments show that the proposed method significantly reduces the number of sampled data needed for RL algorithms.

Design of a Graphical User Interface for Few-Shot Machine Learning Classification of Electron Microscopy Data

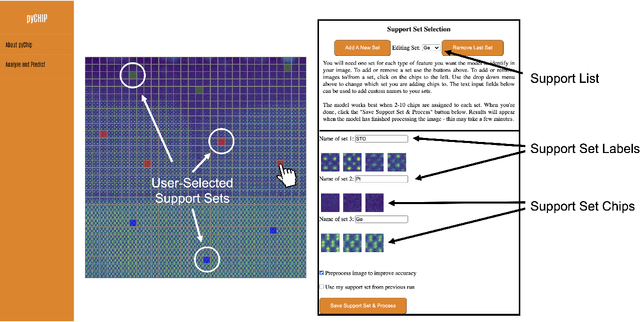
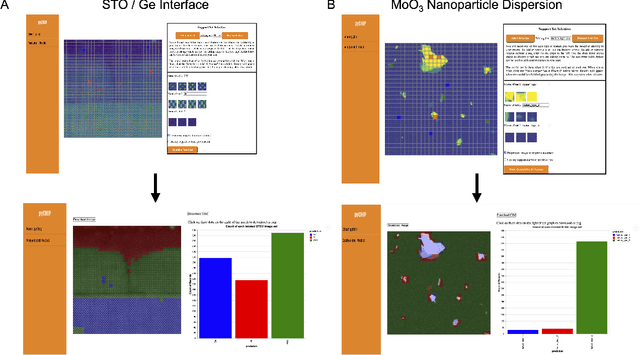
The recent growth in data volumes produced by modern electron microscopes requires rapid, scalable, and flexible approaches to image segmentation and analysis. Few-shot machine learning, which can richly classify images from a handful of user-provided examples, is a promising route to high-throughput analysis. However, current command-line implementations of such approaches can be slow and unintuitive to use, lacking the real-time feedback necessary to perform effective classification. Here we report on the development of a Python-based graphical user interface that enables end users to easily conduct and visualize the output of few-shot learning models. This interface is lightweight and can be hosted locally or on the web, providing the opportunity to reproducibly conduct, share, and crowd-source few-shot analyses.

Lyapunov-Regularized Reinforcement Learning for Power System Transient Stability

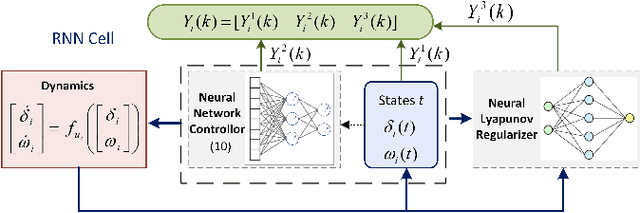
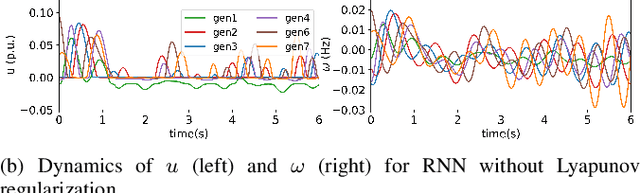
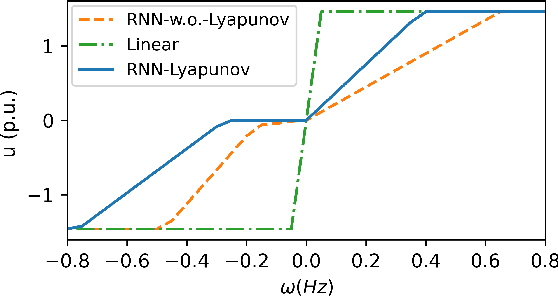
Transient stability of power systems is becoming increasingly important because of the growing integration of renewable resources. These resources lead to a reduction in mechanical inertia but also provide increased flexibility in frequency responses. Namely, their power electronic interfaces can implement almost arbitrary control laws. To design these controllers, reinforcement learning (RL) has emerged as a powerful method in searching for optimal non-linear control policy parameterized by neural networks. A key challenge is to enforce that a learned controller must be stabilizing. This paper proposes a Lyapunov regularized RL approach for optimal frequency control for transient stability in lossy networks. Because the lack of an analytical Lyapunov function, we learn a Lyapunov function parameterized by a neural network. The losses are specially designed with respect to the physical power system. The learned neural Lyapunov function is then utilized as a regularization to train the neural network controller by penalizing actions that violate the Lyapunov conditions. Case study shows that introducing the Lyapunov regularization enables the controller to be stabilizing and achieve smaller losses.