Fast and Reliable $N-k$ Contingency Screening with Input-Convex Neural Networks

Power system operators must ensure that dispatch decisions remain feasible in case of grid outages or contingencies to prevent cascading failures and ensure reliable operation. However, checking the feasibility of all $N - k$ contingencies -- every possible simultaneous failure of $k$ grid components -- is computationally intractable for even small $k$, requiring system operators to resort to heuristic screening methods. Because of the increase in uncertainty and changes in system behaviors, heuristic lists might not include all relevant contingencies, generating false negatives in which unsafe scenarios are misclassified as safe. In this work, we propose to use input-convex neural networks (ICNNs) for contingency screening. We show that ICNN reliability can be determined by solving a convex optimization problem, and by scaling model weights using this problem as a differentiable optimization layer during training, we can learn an ICNN classifier that is both data-driven and has provably guaranteed reliability. Namely, our method can ensure a zero false negative rate. We empirically validate this methodology in a case study on the IEEE 39-bus test network, observing that it yields substantial (10-20x) speedups while having excellent classification accuracy.

Equipping Black-Box Policies with Model-Based Advice for Stable Nonlinear Control

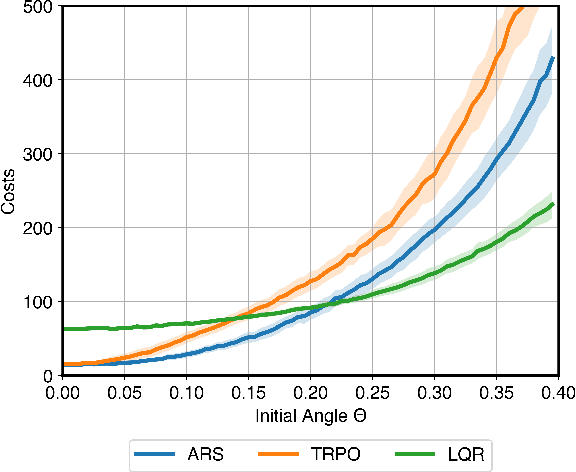
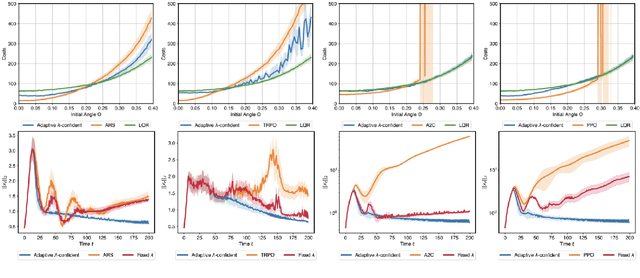
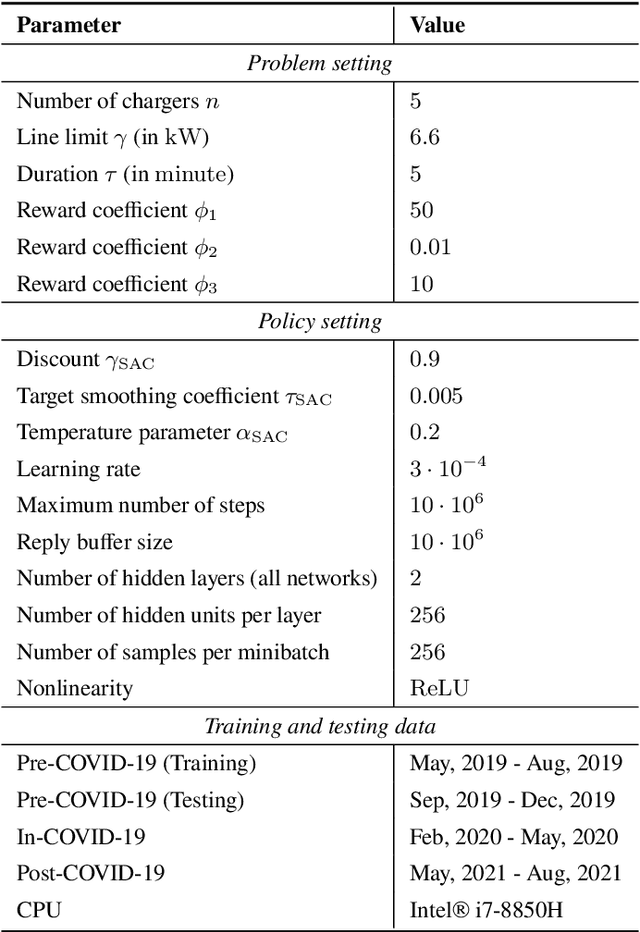
Machine-learned black-box policies are ubiquitous for nonlinear control problems. Meanwhile, crude model information is often available for these problems from, e.g., linear approximations of nonlinear dynamics. We study the problem of equipping a black-box control policy with model-based advice for nonlinear control on a single trajectory. We first show a general negative result that a naive convex combination of a black-box policy and a linear model-based policy can lead to instability, even if the two policies are both stabilizing. We then propose an adaptive $\lambda$-confident policy, with a coefficient $\lambda$ indicating the confidence in a black-box policy, and prove its stability. With bounded nonlinearity, in addition, we show that the adaptive $\lambda$-confident policy achieves a bounded competitive ratio when a black-box policy is near-optimal. Finally, we propose an online learning approach to implement the adaptive $\lambda$-confident policy and verify its efficacy in case studies about the CartPole problem and a real-world electric vehicle (EV) charging problem with data bias due to COVID-19.

Reinforcement Learning for Decision-Making and Control in Power Systems: Tutorial, Review, and Vision

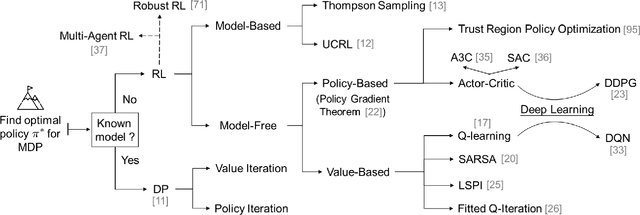
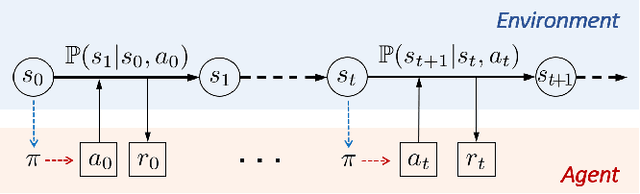
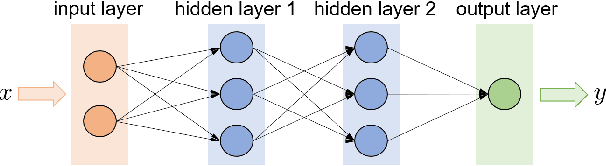
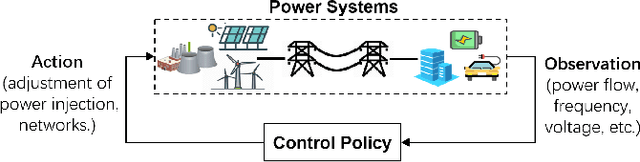
With large-scale integration of renewable generation and ubiquitous distributed energy resources (DERs), modern power systems confront a series of new challenges in operation and control, such as growing complexity, increasing uncertainty, and aggravating volatility. While the upside is that more and more data are available owing to the widely-deployed smart meters, smart sensors, and upgraded communication networks. As a result, data-driven control techniques, especially reinforcement learning (RL), have attracted surging attention in recent years. In this paper, we focus on RL and aim to provide a tutorial on various RL techniques and how they can be applied to the decision-making and control in power systems. In particular, we select three key applications, including frequency regulation, voltage control, and energy management, for illustration, and present the typical ways to model and tackle them with RL methods. We conclude by emphasizing two critical issues in the application of RL, i.e., safety and scalability. Several potential future directions are discussed as well.

Learning Optimal Power Flow: Worst-Case Guarantees for Neural Networks

This paper introduces for the first time a framework to obtain provable worst-case guarantees for neural network performance, using learning for optimal power flow (OPF) problems as a guiding example. Neural networks have the potential to substantially reduce the computing time of OPF solutions. However, the lack of guarantees for their worst-case performance remains a major barrier for their adoption in practice. This work aims to remove this barrier. We formulate mixed-integer linear programs to obtain worst-case guarantees for neural network predictions related to (i) maximum constraint violations, (ii) maximum distances between predicted and optimal decision variables, and (iii) maximum sub-optimality. We demonstrate our methods on a range of PGLib-OPF networks up to 300 buses. We show that the worst-case guarantees can be up to one order of magnitude larger than the empirical lower bounds calculated with conventional methods. More importantly, we show that the worst-case predictions appear at the boundaries of the training input domain, and we demonstrate how we can systematically reduce the worst-case guarantees by training on a larger input domain than the domain they are evaluated on.

Combining Model-Based and Model-Free Methods for Nonlinear Control: A Provably Convergent Policy Gradient Approach

Model-free learning-based control methods have seen great success recently. However, such methods typically suffer from poor sample complexity and limited convergence guarantees. This is in sharp contrast to classical model-based control, which has a rich theory but typically requires strong modeling assumptions. In this paper, we combine the two approaches to achieve the best of both worlds. We consider a dynamical system with both linear and non-linear components and develop a novel approach to use the linear model to define a warm start for a model-free, policy gradient method. We show this hybrid approach outperforms the model-based controller while avoiding the convergence issues associated with model-free approaches via both numerical experiments and theoretical analyses, in which we derive sufficient conditions on the non-linear component such that our approach is guaranteed to converge to the (nearly) global optimal controller.