Equipping Black-Box Policies with Model-Based Advice for Stable Nonlinear Control
Paper and Code
Jun 02, 2022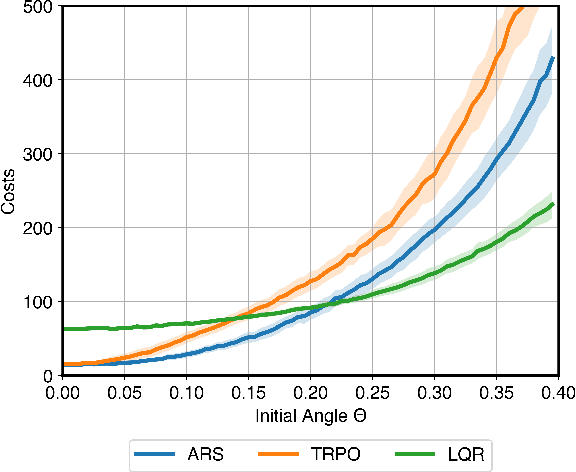

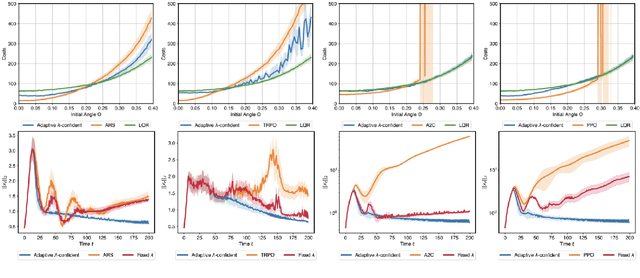
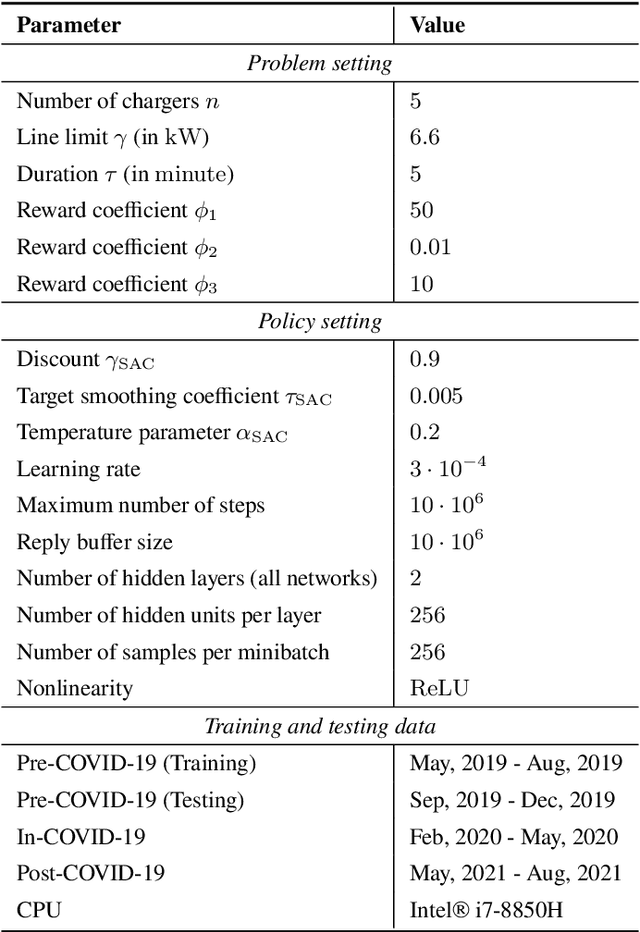
Machine-learned black-box policies are ubiquitous for nonlinear control problems. Meanwhile, crude model information is often available for these problems from, e.g., linear approximations of nonlinear dynamics. We study the problem of equipping a black-box control policy with model-based advice for nonlinear control on a single trajectory. We first show a general negative result that a naive convex combination of a black-box policy and a linear model-based policy can lead to instability, even if the two policies are both stabilizing. We then propose an adaptive $\lambda$-confident policy, with a coefficient $\lambda$ indicating the confidence in a black-box policy, and prove its stability. With bounded nonlinearity, in addition, we show that the adaptive $\lambda$-confident policy achieves a bounded competitive ratio when a black-box policy is near-optimal. Finally, we propose an online learning approach to implement the adaptive $\lambda$-confident policy and verify its efficacy in case studies about the CartPole problem and a real-world electric vehicle (EV) charging problem with data bias due to COVID-19.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge