OmniAD: Detect and Understand Industrial Anomaly via Multimodal Reasoning

While anomaly detection has made significant progress, generating detailed analyses that incorporate industrial knowledge remains a challenge. To address this gap, we introduce OmniAD, a novel framework that unifies anomaly detection and understanding for fine-grained analysis. OmniAD is a multimodal reasoner that combines visual and textual reasoning processes. The visual reasoning provides detailed inspection by leveraging Text-as-Mask Encoding to perform anomaly detection through text generation without manually selected thresholds. Following this, Visual Guided Textual Reasoning conducts comprehensive analysis by integrating visual perception. To enhance few-shot generalization, we employ an integrated training strategy that combines supervised fine-tuning (SFT) with reinforcement learning (GRPO), incorporating three sophisticated reward functions. Experimental results demonstrate that OmniAD achieves a performance of 79.1 on the MMAD benchmark, surpassing models such as Qwen2.5-VL-7B and GPT-4o. It also shows strong results across multiple anomaly detection benchmarks. These results highlight the importance of enhancing visual perception for effective reasoning in anomaly understanding. All codes and models will be publicly available.

AlignGen: Boosting Personalized Image Generation with Cross-Modality Prior Alignment

Personalized image generation aims to integrate user-provided concepts into text-to-image models, enabling the generation of customized content based on a given prompt. Recent zero-shot approaches, particularly those leveraging diffusion transformers, incorporate reference image information through multi-modal attention mechanism. This integration allows the generated output to be influenced by both the textual prior from the prompt and the visual prior from the reference image. However, we observe that when the prompt and reference image are misaligned, the generated results exhibit a stronger bias toward the textual prior, leading to a significant loss of reference content. To address this issue, we propose AlignGen, a Cross-Modality Prior Alignment mechanism that enhances personalized image generation by: 1) introducing a learnable token to bridge the gap between the textual and visual priors, 2) incorporating a robust training strategy to ensure proper prior alignment, and 3) employing a selective cross-modal attention mask within the multi-modal attention mechanism to further align the priors. Experimental results demonstrate that AlignGen outperforms existing zero-shot methods and even surpasses popular test-time optimization approaches.

DCEdit: Dual-Level Controlled Image Editing via Precisely Localized Semantics

This paper presents a novel approach to improving text-guided image editing using diffusion-based models. Text-guided image editing task poses key challenge of precisly locate and edit the target semantic, and previous methods fall shorts in this aspect. Our method introduces a Precise Semantic Localization strategy that leverages visual and textual self-attention to enhance the cross-attention map, which can serve as a regional cues to improve editing performance. Then we propose a Dual-Level Control mechanism for incorporating regional cues at both feature and latent levels, offering fine-grained control for more precise edits. To fully compare our methods with other DiT-based approaches, we construct the RW-800 benchmark, featuring high resolution images, long descriptive texts, real-world images, and a new text editing task. Experimental results on the popular PIE-Bench and RW-800 benchmarks demonstrate the superior performance of our approach in preserving background and providing accurate edits.

Memory Efficient Matting with Adaptive Token Routing

Transformer-based models have recently achieved outstanding performance in image matting. However, their application to high-resolution images remains challenging due to the quadratic complexity of global self-attention. To address this issue, we propose MEMatte, a \textbf{m}emory-\textbf{e}fficient \textbf{m}atting framework for processing high-resolution images. MEMatte incorporates a router before each global attention block, directing informative tokens to the global attention while routing other tokens to a Lightweight Token Refinement Module (LTRM). Specifically, the router employs a local-global strategy to predict the routing probability of each token, and the LTRM utilizes efficient modules to simulate global attention. Additionally, we introduce a Batch-constrained Adaptive Token Routing (BATR) mechanism, which allows each router to dynamically route tokens based on image content and the stages of attention block in the network. Furthermore, we construct an ultra high-resolution image matting dataset, UHR-395, comprising 35,500 training images and 1,000 test images, with an average resolution of $4872\times6017$. This dataset is created by compositing 395 different alpha mattes across 11 categories onto various backgrounds, all with high-quality manual annotation. Extensive experiments demonstrate that MEMatte outperforms existing methods on both high-resolution and real-world datasets, significantly reducing memory usage by approximately 88% and latency by 50% on the Composition-1K benchmark. Our code is available at https://github.com/linyiheng123/MEMatte.

Approximate Global Convergence of Independent Learning in Multi-Agent Systems

Independent learning (IL), despite being a popular approach in practice to achieve scalability in large-scale multi-agent systems, usually lacks global convergence guarantees. In this paper, we study two representative algorithms, independent $Q$-learning and independent natural actor-critic, within value-based and policy-based frameworks, and provide the first finite-sample analysis for approximate global convergence. The results imply a sample complexity of $\tilde{\mathcal{O}}(\epsilon^{-2})$ up to an error term that captures the dependence among agents and characterizes the fundamental limit of IL in achieving global convergence. To establish the result, we develop a novel approach for analyzing IL by constructing a separable Markov decision process (MDP) for convergence analysis and then bounding the gap due to model difference between the separable MDP and the original one. Moreover, we conduct numerical experiments using a synthetic MDP and an electric vehicle charging example to verify our theoretical findings and to demonstrate the practical applicability of IL.

Diffusion for Natural Image Matting

We aim to leverage diffusion to address the challenging image matting task. However, the presence of high computational overhead and the inconsistency of noise sampling between the training and inference processes pose significant obstacles to achieving this goal. In this paper, we present DiffMatte, a solution designed to effectively overcome these challenges. First, DiffMatte decouples the decoder from the intricately coupled matting network design, involving only one lightweight decoder in the iterations of the diffusion process. With such a strategy, DiffMatte mitigates the growth of computational overhead as the number of samples increases. Second, we employ a self-aligned training strategy with uniform time intervals, ensuring a consistent noise sampling between training and inference across the entire time domain. Our DiffMatte is designed with flexibility in mind and can seamlessly integrate into various modern matting architectures. Extensive experimental results demonstrate that DiffMatte not only reaches the state-of-the-art level on the Composition-1k test set, surpassing the best methods in the past by 5% and 15% in the SAD metric and MSE metric respectively, but also show stronger generalization ability in other benchmarks.

Beyond Black-Box Advice: Learning-Augmented Algorithms for MDPs with Q-Value Predictions

We study the tradeoff between consistency and robustness in the context of a single-trajectory time-varying Markov Decision Process (MDP) with untrusted machine-learned advice. Our work departs from the typical approach of treating advice as coming from black-box sources by instead considering a setting where additional information about how the advice is generated is available. We prove a first-of-its-kind consistency and robustness tradeoff given Q-value advice under a general MDP model that includes both continuous and discrete state/action spaces. Our results highlight that utilizing Q-value advice enables dynamic pursuit of the better of machine-learned advice and a robust baseline, thus result in near-optimal performance guarantees, which provably improves what can be obtained solely with black-box advice.

Convergence Rates for Localized Actor-Critic in Networked Markov Potential Games

We introduce a class of networked Markov potential games where agents are associated with nodes in a network. Each agent has its own local potential function, and the reward of each agent depends only on the states and actions of agents within a $\kappa$-hop neighborhood. In this context, we propose a localized actor-critic algorithm. The algorithm is scalable since each agent uses only local information and does not need access to the global state. Further, the algorithm overcomes the curse of dimensionality through the use of function approximation. Our main results provide finite-sample guarantees up to a localization error and a function approximation error. Specifically, we achieve an $\tilde{\mathcal{O}}(\epsilon^{-4})$ sample complexity measured by the averaged Nash regret. This is the first finite-sample bound for multi-agent competitive games that does not depend on the number of agents.

Global Convergence of Localized Policy Iteration in Networked Multi-Agent Reinforcement Learning

We study a multi-agent reinforcement learning (MARL) problem where the agents interact over a given network. The goal of the agents is to cooperatively maximize the average of their entropy-regularized long-term rewards. To overcome the curse of dimensionality and to reduce communication, we propose a Localized Policy Iteration (LPI) algorithm that provably learns a near-globally-optimal policy using only local information. In particular, we show that, despite restricting each agent's attention to only its $\kappa$-hop neighborhood, the agents are able to learn a policy with an optimality gap that decays polynomially in $\kappa$. In addition, we show the finite-sample convergence of LPI to the global optimal policy, which explicitly captures the trade-off between optimality and computational complexity in choosing $\kappa$. Numerical simulations demonstrate the effectiveness of LPI.

Equipping Black-Box Policies with Model-Based Advice for Stable Nonlinear Control

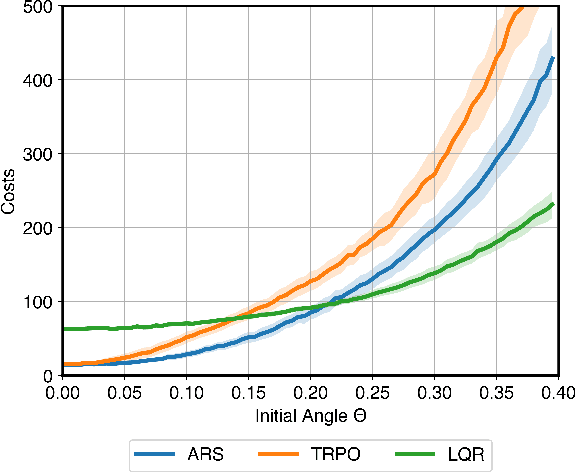
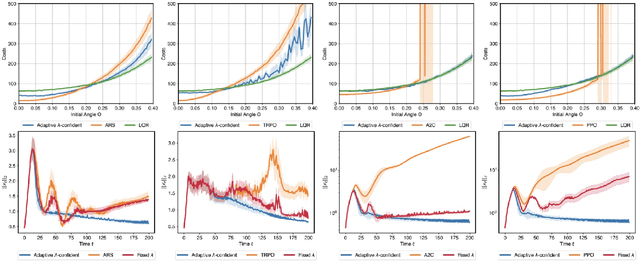
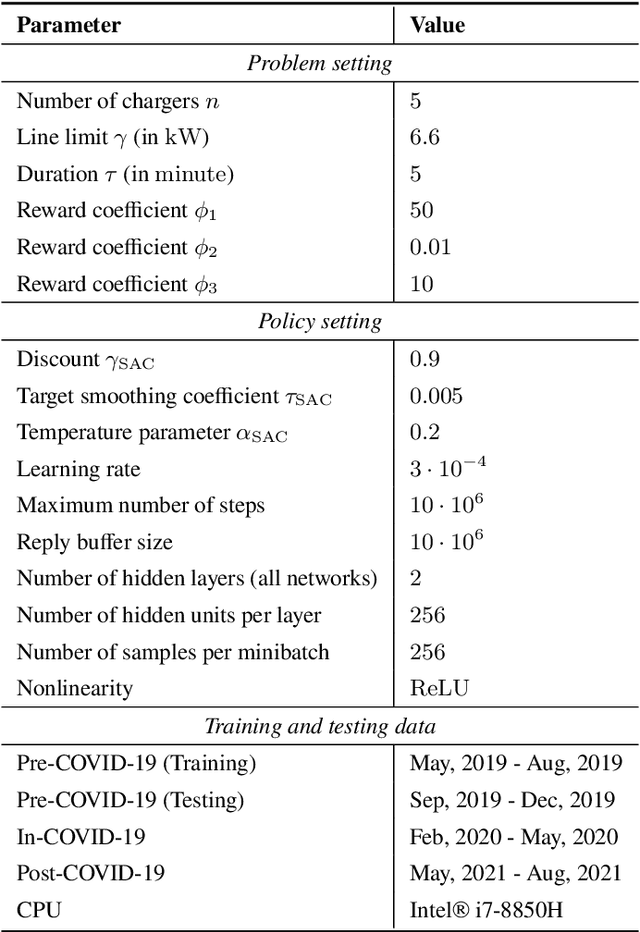
Machine-learned black-box policies are ubiquitous for nonlinear control problems. Meanwhile, crude model information is often available for these problems from, e.g., linear approximations of nonlinear dynamics. We study the problem of equipping a black-box control policy with model-based advice for nonlinear control on a single trajectory. We first show a general negative result that a naive convex combination of a black-box policy and a linear model-based policy can lead to instability, even if the two policies are both stabilizing. We then propose an adaptive $\lambda$-confident policy, with a coefficient $\lambda$ indicating the confidence in a black-box policy, and prove its stability. With bounded nonlinearity, in addition, we show that the adaptive $\lambda$-confident policy achieves a bounded competitive ratio when a black-box policy is near-optimal. Finally, we propose an online learning approach to implement the adaptive $\lambda$-confident policy and verify its efficacy in case studies about the CartPole problem and a real-world electric vehicle (EV) charging problem with data bias due to COVID-19.