Revisiting Policy Gradients for Restricted Policy Classes: Escaping Myopic Local Optima with $k$-step Policy Gradients

This work revisits standard policy gradient methods used on restricted policy classes, which are known to get stuck in suboptimal critical points. We identify an important cause for this phenomenon to be that the policy gradient is itself fundamentally myopic, i.e. it only improves the policy based on the one-step $Q$-function. In this work, we propose a generalized $k$-step policy gradient method that couples the randomness within a $k$-step time window and can escape the myopic local optima in MDPs with restricted policy classes. We show this new method is theoretically guaranteed to converge to a solution that is exponentially close in performance to the optimal deterministic policy with respect to $k$. Further, we show projected gradient descent and mirror descent with this $k$-step policy gradient can achieve this exponential guarantee in $O(\frac{1}{T})$ iterations, despite only assuming smoothness and differentiability of the value function. This will provide near optimal solutions to previously elusive applications like state aggregation and partially observable cooperative multi-agent settings. Moreover, our bounds avoid the ubiquitous distribution mismatch factors $||d_μ^{π^*} / d_μ^π||_\infty$ and $||d_μ^{π^*} / μ||_\infty$ enabling the $k$-step policy gradient method to escape suboptimal critical points that emerge from poor exploration in fully observable settings.

Towards Effective Theory of LLMs: A Representation Learning Approach

We propose Representational Effective Theory (RET), a framework for describing large language model computation in terms of learned macrostates rather than microscopic details. RET learns these macrostates from hidden-state trajectories using a BYOL/JEPA-style self-supervised objective, coarse-graining activations into macrovariables that preserve higher-level structure relevant for prediction and interpretation. We evaluate whether these macrovariables are practically relevant for interpretability: RET yields temporally consistent states that reveal "mental-state" trajectories of reasoning, capture high-level semantic structure, support early prediction of behavioral outcomes such as sycophancy, and provide causal handles for steering generations toward interpretable computational phases. Together, these results suggest that LLM computation admits useful effective descriptions via RET: high-level, dynamically meaningful variables that support interpretation, prediction, and intervention.

BLOCK-EM: Preventing Emergent Misalignment by Blocking Causal Features

Emergent misalignment can arise when a language model is fine-tuned on a narrowly scoped supervised objective: the model learns the target behavior, yet also develops undesirable out-of-domain behaviors. We investigate a mechanistic approach to preventing emergent misalignment by identifying a small set of internal features that reliably control the misaligned behavior and then discouraging the model from strengthening these features during fine-tuning. Across six fine-tuning domains, blocking (i.e., constraining) a fixed set of features achieves up to 95\% relative reduction in emergent misalignment with no degradation in model quality or target-task performance. We strengthen validity with disjoint selection/evaluation splits, multiple independent judges, multiple random seeds for key settings, quality metrics, and extensive ablations demonstrating that the reduction in misalignment is specific to the identified mechanism. We also characterize a limiting regime in which misalignment re-emerges under prolonged fine-tuning, present evidence consistent with rerouting through alternative features or layers, and evaluate modifications that partially restore the misalignment-blocking effect. Overall, our results show that targeted training-time constraints on internal mechanisms can mitigate emergent misalignment without degrading target-task performance.

Polynomial Convergence of Riemannian Diffusion Models

Diffusion models have demonstrated remarkable empirical success in the recent years and are considered one of the state-of-the-art generative models in modern AI. These models consist of a forward process, which gradually diffuses the data distribution to a noise distribution spanning the whole space, and a backward process, which inverts this transformation to recover the data distribution from noise. Most of the existing literature assumes that the underlying space is Euclidean. However, in many practical applications, the data are constrained to lie on a submanifold of Euclidean space. Addressing this setting, De Bortoli et al. (2022) introduced Riemannian diffusion models and proved that using an exponentially small step size yields a small sampling error in the Wasserstein distance, provided the data distribution is smooth and strictly positive, and the score estimate is $L_\infty$-accurate. In this paper, we greatly strengthen this theory by establishing that, under $L_2$-accurate score estimate, a {\em polynomially small stepsize} suffices to guarantee small sampling error in the total variation distance, without requiring smoothness or positivity of the data distribution. Our analysis only requires mild and standard curvature assumptions on the underlying manifold. The main ingredients in our analysis are Li-Yau estimate for the log-gradient of heat kernel, and Minakshisundaram-Pleijel parametrix expansion of the perturbed heat equation. Our approach opens the door to a sharper analysis of diffusion models on non-Euclidean spaces.

Transformer-Based Scalable Multi-Agent Reinforcement Learning for Networked Systems with Long-Range Interactions

Multi-agent reinforcement learning (MARL) has shown promise for large-scale network control, yet existing methods face two major limitations. First, they typically rely on assumptions leading to decay properties of local agent interactions, limiting their ability to capture long-range dependencies such as cascading power failures or epidemic outbreaks. Second, most approaches lack generalizability across network topologies, requiring retraining when applied to new graphs. We introduce STACCA (Shared Transformer Actor-Critic with Counterfactual Advantage), a unified transformer-based MARL framework that addresses both challenges. STACCA employs a centralized Graph Transformer Critic to model long-range dependencies and provide system-level feedback, while its shared Graph Transformer Actor learns a generalizable policy capable of adapting across diverse network structures. Further, to improve credit assignment during training, STACCA integrates a novel counterfactual advantage estimator that is compatible with state-value critic estimates. We evaluate STACCA on epidemic containment and rumor-spreading network control tasks, demonstrating improved performance, network generalization, and scalability. These results highlight the potential of transformer-based MARL architectures to achieve scalable and generalizable control in large-scale networked systems.

Comparative Field Deployment of Reinforcement Learning and Model Predictive Control for Residential HVAC

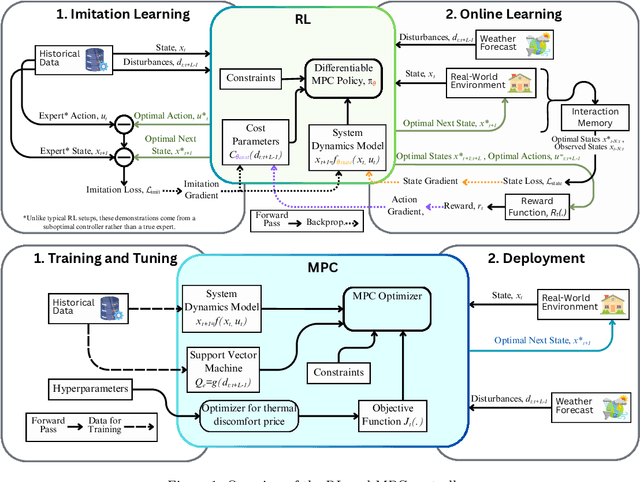
Advanced control strategies like Model Predictive Control (MPC) offer significant energy savings for HVAC systems but often require substantial engineering effort, limiting scalability. Reinforcement Learning (RL) promises greater automation and adaptability, yet its practical application in real-world residential settings remains largely undemonstrated, facing challenges related to safety, interpretability, and sample efficiency. To investigate these practical issues, we performed a direct comparison of an MPC and a model-based RL controller, with each controller deployed for a one-month period in an occupied house with a heat pump system in West Lafayette, Indiana. This investigation aimed to explore scalability of the chosen RL and MPC implementations while ensuring safety and comparability. The advanced controllers were evaluated against each other and against the existing controller. RL achieved substantial energy savings (22\% relative to the existing controller), slightly exceeding MPC's savings (20\%), albeit with modestly higher occupant discomfort. However, when energy savings were normalized for the level of comfort provided, MPC demonstrated superior performance. This study's empirical results show that while RL reduces engineering overhead, it introduces practical trade-offs in model accuracy and operational robustness. The key lessons learned concern the difficulties of safe controller initialization, navigating the mismatch between control actions and their practical implementation, and maintaining the integrity of online learning in a live environment. These insights pinpoint the essential research directions needed to advance RL from a promising concept to a truly scalable HVAC control solution.

A Theoretical Study of (Hyper) Self-Attention through the Lens of Interactions: Representation, Training, Generalization

Self-attention has emerged as a core component of modern neural architectures, yet its theoretical underpinnings remain elusive. In this paper, we study self-attention through the lens of interacting entities, ranging from agents in multi-agent reinforcement learning to alleles in genetic sequences, and show that a single layer linear self-attention can efficiently represent, learn, and generalize functions capturing pairwise interactions, including out-of-distribution scenarios. Our analysis reveals that self-attention acts as a mutual interaction learner under minimal assumptions on the diversity of interaction patterns observed during training, thereby encompassing a wide variety of real-world domains. In addition, we validate our theoretical insights through experiments demonstrating that self-attention learns interaction functions and generalizes across both population distributions and out-of-distribution scenarios. Building on our theories, we introduce HyperFeatureAttention, a novel neural network module designed to learn couplings of different feature-level interactions between entities. Furthermore, we propose HyperAttention, a new module that extends beyond pairwise interactions to capture multi-entity dependencies, such as three-way, four-way, or general n-way interactions.

Thinking Beyond Visibility: A Near-Optimal Policy Framework for Locally Interdependent Multi-Agent MDPs

Decentralized Partially Observable Markov Decision Processes (Dec-POMDPs) are known to be NEXP-Complete and intractable to solve. However, for problems such as cooperative navigation, obstacle avoidance, and formation control, basic assumptions can be made about local visibility and local dependencies. The work DeWeese and Qu 2024 formalized these assumptions in the construction of the Locally Interdependent Multi-Agent MDP. In this setting, it establishes three closed-form policies that are tractable to compute in various situations and are exponentially close to optimal with respect to visibility. However, it is also shown that these solutions can have poor performance when the visibility is small and fixed, often getting stuck during simulations due to the so called "Penalty Jittering" phenomenon. In this work, we establish the Extended Cutoff Policy Class which is, to the best of our knowledge, the first non-trivial class of near optimal closed-form partially observable policies that are exponentially close to optimal with respect to the visibility for any Locally Interdependent Multi-Agent MDP. These policies are able to remember agents beyond their visibilities which allows them to perform significantly better in many small and fixed visibility settings, resolve Penalty Jittering occurrences, and under certain circumstances guarantee fully observable joint optimal behavior despite the partial observability. We also propose a generalized form of the Locally Interdependent Multi-Agent MDP that allows for transition dependence and extended reward dependence, then replicate our theoretical results in this setting.

Natural Policy Gradient for Average Reward Non-Stationary RL

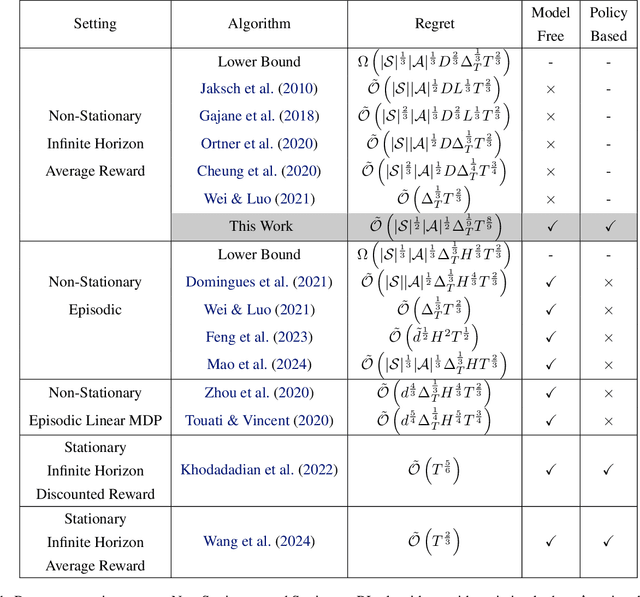
We consider the problem of non-stationary reinforcement learning (RL) in the infinite-horizon average-reward setting. We model it by a Markov Decision Process with time-varying rewards and transition probabilities, with a variation budget of $\Delta_T$. Existing non-stationary RL algorithms focus on model-based and model-free value-based methods. Policy-based methods despite their flexibility in practice are not theoretically well understood in non-stationary RL. We propose and analyze the first model-free policy-based algorithm, Non-Stationary Natural Actor-Critic (NS-NAC), a policy gradient method with a restart based exploration for change and a novel interpretation of learning rates as adapting factors. Further, we present a bandit-over-RL based parameter-free algorithm BORL-NS-NAC that does not require prior knowledge of the variation budget $\Delta_T$. We present a dynamic regret of $\tilde{\mathscr O}(|S|^{1/2}|A|^{1/2}\Delta_T^{1/6}T^{5/6})$ for both algorithms, where $T$ is the time horizon, and $|S|$, $|A|$ are the sizes of the state and action spaces. The regret analysis leverages a novel adaptation of the Lyapunov function analysis of NAC to dynamic environments and characterizes the effects of simultaneous updates in policy, value function estimate and changes in the environment.

Whole-Body Model-Predictive Control of Legged Robots with MuJoCo

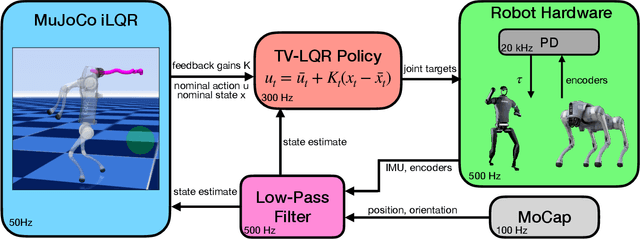
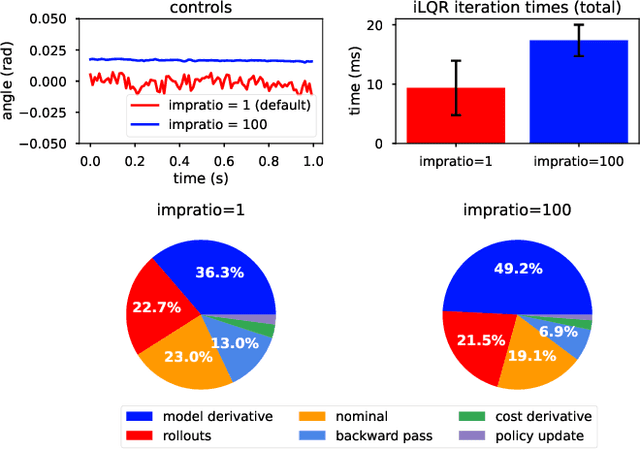
We demonstrate the surprising real-world effectiveness of a very simple approach to whole-body model-predictive control (MPC) of quadruped and humanoid robots: the iterative LQR (iLQR) algorithm with MuJoCo dynamics and finite-difference approximated derivatives. Building upon the previous success of model-based behavior synthesis and control of locomotion and manipulation tasks with MuJoCo in simulation, we show that these policies can easily generalize to the real world with few sim-to-real considerations. Our baseline method achieves real-time whole-body MPC on a variety of hardware experiments, including dynamic quadruped locomotion, quadruped walking on two legs, and full-sized humanoid bipedal locomotion. We hope this easy-to-reproduce hardware baseline lowers the barrier to entry for real-world whole-body MPC research and contributes to accelerating research velocity in the community. Our code and experiment videos will be available online at:https://johnzhang3.github.io/mujoco_ilqr